|
Dicke State
In quantum optics and quantum information, a Dicke state is a quantum state defined by Robert H. Dicke in connection to spontaneous radiation processes taking place in an ensemble of two-state atoms. A Dicke state is the simultaneous eigenstate of the angular momentum operators ^2 and J_z. Dicke states have recently been realized with photons with up to six particles and cold atoms of more than thousands of particles. They are highly entangled, and in quantum metrology they lead to the maximal Heisenberg scaling of the precision of parameter estimation. Defining equations Dicke states are defined in a system of N spin-s particles as the simultaneous eigenstates of the angular momentum operators ^2 and J_z by the equations : ^2, j,j_z,\alpha\rangle = j(j+1), j,j_z,\alpha\rangle and : J_z , j,j_z,\alpha\rangle = j_z, j,j_z,\alpha\rangle. Here, \alpha is a label used to distinguish several states orthogonal to each other, for which the two eigenvalues are the same. It i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Optics
Quantum optics is a branch of atomic, molecular, and optical physics and quantum chemistry that studies the behavior of photons (individual quanta of light). It includes the study of the particle-like properties of photons and their interaction with, for instance, atoms and molecules. Photons have been used to test many of the counter-intuitive predictions of quantum mechanics, such as entanglement and teleportation, and are a useful resource for quantum information processing. History Light propagating in a restricted volume of space has its energy and momentum quantized according to an integer number of particles known as photons. Quantum optics studies the nature and effects of light as quantized photons. The first major development leading to that understanding was the correct modeling of the blackbody radiation spectrum by Max Planck in 1899 under the hypothesis of light being emitted in discrete units of energy. The photoelectric effect was further evidence of thi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Information
Quantum information is the information of the state of a quantum system. It is the basic entity of study in quantum information theory, and can be manipulated using quantum information processing techniques. Quantum information refers to both the technical definition in terms of Von Neumann entropy and the general computational term. It is an interdisciplinary field that involves quantum mechanics, computer science, information theory, philosophy and cryptography among other fields. Its study is also relevant to disciplines such as cognitive science, psychology and neuroscience. Its main focus is in extracting information from matter at the microscopic scale. Observation in science is one of the most important ways of acquiring information and measurement is required in order to quantify the observation, making this crucial to the scientific method. In quantum mechanics, due to the uncertainty principle, non-commuting observables cannot be precisely measured simultaneously, as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Robert H
The name Robert is an ancient Germanic given name, from Proto-Germanic "fame" and "bright" (''Hrōþiberhtaz''). Compare Old Dutch ''Robrecht'' and Old High German ''Hrodebert'' (a compound of ''Hrōþ, Hruod'' () "fame, glory, honour, praise, renown, godlike" and ''berht'' "bright, light, shining"). It is the second most frequently used given name of ancient Germanic origin.Reaney & Wilson, 1997. ''Dictionary of English Surnames''. Oxford University Press. It is also in use Robert (surname), as a surname. Another commonly used form of the name is Rupert (name), Rupert. After becoming widely used in Continental Europe, the name entered England in its Old French form ''Robert'', where an Old English cognate form (''Hrēodbēorht'', ''Hrodberht'', ''Hrēodbēorð'', ''Hrœdbœrð'', ''Hrœdberð'', ''Hrōðberχtŕ'') had existed before the Norman Conquest. The feminine version is Roberta (given name), Roberta. The Italian, Portuguese, and Spanish form is Roberto (given name), ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Permutationally Invariant Quantum State Tomography
Permutationally invariant quantum state tomography (PI quantum state tomography) is a method for the partial determination of the state of a quantum system consisting of many subsystems. In general, the number of parameters needed to describe the quantum mechanical state of a system consisting of N subsystems is increasing exponentially with N. For instance, for an N-qubit system, 2^-2 real parameters are needed to describe the state vector of a pure state, or 2^ -1 real parameters are needed to describe the density matrix of a mixed state. '' Quantum state tomography'' is a method to determine all these parameters from a series of measurements on many independent and identically prepared systems. Thus, in the case of full quantum state tomography, the number of measurements needed scales exponentially with the number of particles or qubits. For large systems, the determination of the entire quantum state is no longer possible in practice and one is interested in methods that ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multipartite Entanglement
In the case of systems composed of m > 2 subsystems, the classification of quantum-entangled states is richer than in the bipartite case. Indeed, in multipartite entanglement apart from fully separable states and fully entangled states, there also exists the notion of partially separable states. Full and partial separability The definitions of fully separable and fully entangled multipartite states naturally generalizes that of separable and entangled states in the bipartite case, as follows. Full ''m''-partite separability (''m''-separability) of ''m'' systems The state \; \varrho_ of \; m subsystems \; A_1, \ldots, A_m with Hilbert space \; \mathcal_=\mathcal_\otimes\ldots\otimes \mathcal_ is fully separable if and only if it can be written in the form :\; \varrho_ = \sum_^k p_i \varrho_^i \otimes \ldots \otimes \varrho_^i. Correspondingly, the state \; \varrho_ is fully entangled if it cannot be written in the above form. As in the bipartite case, the set of \; m-sep ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Entanglement Depth
In quantum physics, entanglement depth characterizes the strength of multiparticle entanglement. An entanglement depth k means that the quantum state of a particle ensemble cannot be described under the assumption that particles interacted with each other only in groups having fewer than k particles. It has been used to characterize the quantum states created in experiments with cold gases. Definition Entanglement depth appeared in the context of spin squeezing. It turned out that to achieve larger and larger spin squeezing, and thus larger and larger precision in parameter estimation, a larger and larger entanglement depth is needed. Later it was formalized in terms of convex sets of quantum states, independent of spin squeezing as follows. Let us consider a pure state that is the tensor product of multi-particle quantum states , \Psi\rangle=, \phi_1\rangle\otimes, \phi_2\rangle\otimes ... \otimes, \phi_n\rangle. The pure state , \Psi\rangle is said to be k-producibl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Fisher Information
The quantum Fisher information is a central quantity in quantum metrology and is the quantum analogue of the classical Fisher information. It is one of the central quantities used to qualify the utility of an input state, especially in Mach–Zehnder (or, equivalently, Ramsey) interferometer-based phase or parameter estimation. It is shown that the quantum Fisher information can also be a sensitive probe of a quantum phase transition (e.g. recognizing the superradiant quantum phase transition in the Dicke model). The quantum Fisher information F_[\varrho,A] of a quantum state, state \varrho with respect to the quantum observable, observable A is defined as : F_[\varrho,A]=2\sum_ \frac \vert \langle k \vert A \vert l\rangle \vert^2, where \lambda_k and \vert k \rangle are the eigenvalues and eigenvectors of the density matrix \varrho, respectively, and the summation goes over all k and l such that \lambda_k+\lambda_l>0. When the observable generates a unitarity (physics), unita ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Greenberger–Horne–Zeilinger State
In physics, in the area of quantum information theory, a Greenberger–Horne–Zeilinger (GHZ) state is an entangled quantum state that involves at least three subsystems (particle states, qubits, or qudits). Named for the three authors that first described this state, the GHZ state predicts outcomes from experiments that directly contradict predictions by every classical local hidden-variable theory. The state has applications in quantum computing. History The four-particle version was first studied by Daniel Greenberger, Michael Horne and Anton Zeilinger in 1989. The following year Abner Shimony joined in and they published a three-particle version based on suggestions by N. David Mermin. Experimental measurements on such states contradict intuitive notions of locality and causality. GHZ states for large numbers of qubits are theorized to give enhanced performance for metrology compared to other qubit superposition states. Definition The GHZ state is an entangled q ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multipartite Entanglement
In the case of systems composed of m > 2 subsystems, the classification of quantum-entangled states is richer than in the bipartite case. Indeed, in multipartite entanglement apart from fully separable states and fully entangled states, there also exists the notion of partially separable states. Full and partial separability The definitions of fully separable and fully entangled multipartite states naturally generalizes that of separable and entangled states in the bipartite case, as follows. Full ''m''-partite separability (''m''-separability) of ''m'' systems The state \; \varrho_ of \; m subsystems \; A_1, \ldots, A_m with Hilbert space \; \mathcal_=\mathcal_\otimes\ldots\otimes \mathcal_ is fully separable if and only if it can be written in the form :\; \varrho_ = \sum_^k p_i \varrho_^i \otimes \ldots \otimes \varrho_^i. Correspondingly, the state \; \varrho_ is fully entangled if it cannot be written in the above form. As in the bipartite case, the set of \; m-sep ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
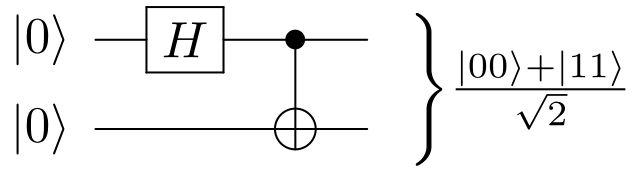
Bell State
In quantum information science, the Bell's states or EPR pairs are specific quantum states of two qubits that represent the simplest examples of quantum entanglement. The Bell's states are a form of entangled and normalized basis vectors. This normalization implies that the overall probability of the particles being in one of the mentioned states is 1: \langle \Phi, \Phi \rangle = 1. Entanglement is a basis-independent result of superposition. Due to this superposition, measurement of the qubit will " collapse" it into one of its basis states with a given probability. Because of the entanglement, measurement of one qubit will "collapse" the other qubit to a state whose measurement will yield one of two possible values, where the value depends on which Bell's state the two qubits are in initially. Bell's states can be generalized to certain quantum states of multi-qubit systems, such as the GHZ state for three or more subsystems. Understanding of Bell's states is useful in a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Graph State
In quantum computing, a graph state is a special type of multi-qubit state that can be represented by a graph. Each qubit is represented by a vertex of the graph, and there is an edge between every interacting pair of qubits. In particular, they are a convenient way of representing certain types of entangled states. Graph states are useful in quantum error-correcting codes, entanglement measurement and purification and for characterization of computational resources in measurement based quantum computing models. A graph state is a particular case of a stabilizer state as well as a 2-uniform hypergraph state, a generalization where the edges have cardinality between 1 and N. Formal definition Quantum graph states can be defined in two equivalent ways: through the notion of quantum circuits and stabilizer formalism. Quantum circuit definition Given a graph G = (V, E), with the set of vertices V and the set of edges E, the corresponding graph state is defined as : =\prod _ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cluster State
In quantum information and quantum computing, a cluster state is a type of highly entangled state of multiple qubits. Cluster states are generated in lattices of qubits with Ising type interactions. A cluster ''C'' is a connected subset of a ''d''-dimensional lattice, and a cluster state is a pure state of the qubits located on ''C''. They are different from other types of entangled states such as GHZ states or W states in that it is more difficult to eliminate quantum entanglement (via projective measurements) in the case of cluster states. Another way of thinking of cluster states is as a particular instance of graph states, where the underlying graph is a connected subset of a ''d''-dimensional lattice. Cluster states are especially useful in the context of the one-way quantum computer. For a comprehensible introduction to the topic see . Formally, cluster states , \phi_\rangle_ are states which obey the set eigenvalue equations: : K^ =(-1)^ where K^ are the correlati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |