|
Cluster State
In quantum information and quantum computing, a cluster state is a type of highly entangled state of multiple qubits. Cluster states are generated in lattices of qubits with Ising type interactions. A cluster ''C'' is a connected subset of a ''d''-dimensional lattice, and a cluster state is a pure state of the qubits located on ''C''. They are different from other types of entangled states such as GHZ states or W states in that it is more difficult to eliminate quantum entanglement (via projective measurements) in the case of cluster states. Another way of thinking of cluster states is as a particular instance of graph states, where the underlying graph is a connected subset of a ''d''-dimensional lattice. Cluster states are especially useful in the context of the one-way quantum computer. For a comprehensible introduction to the topic see . Formally, cluster states , \phi_\rangle_ are states which obey the set eigenvalue equations: : K^ =(-1)^ where K^ are the correlati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Quantum Information
Quantum information is the information of the state of a quantum system. It is the basic entity of study in quantum information theory, and can be manipulated using quantum information processing techniques. Quantum information refers to both the technical definition in terms of Von Neumann entropy and the general computational term. It is an interdisciplinary field that involves quantum mechanics, computer science, information theory, philosophy and cryptography among other fields. Its study is also relevant to disciplines such as cognitive science, psychology and neuroscience. Its main focus is in extracting information from matter at the microscopic scale. Observation in science is one of the most important ways of acquiring information and measurement is required in order to quantify the observation, making this crucial to the scientific method. In quantum mechanics, due to the uncertainty principle, non-commuting observables cannot be precisely measured simultaneously, as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
 |
Spontaneous Parametric Down-conversion
Spontaneous parametric down-conversion (also known as SPDC, parametric fluorescence or parametric scattering) is a nonlinear instant optical process that converts one photon of higher energy (namely, a ''pump'' photon) into a pair of photons (namely, ''signal'' and ''idler'' photons) of lower energy, in accordance with the laws of law of conservation of energy, energy conservation and law of conservation of momentum, momentum conservation. It is an important process in quantum optics, for the generation of photon entanglement, entangled photon pairs and of single photons. Description A Nonlinear optics, nonlinear crystal is used to produce pairs of photons from a photon beam. In accordance with conservations of energy and momentum, the pairs need to have combined energies and momenta equal to the energy and momentum of the original photon. Because the index of refraction changes with frequency (Dispersion (optics), dispersion), only certain triplets of frequencies will be phase ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
Dicke State
In quantum optics and quantum information, a Dicke state is a quantum state defined by Robert H. Dicke in connection to spontaneous radiation processes taking place in an ensemble of two-state atoms. A Dicke state is the simultaneous eigenstate of the angular momentum operators ^2 and J_z. Dicke states have recently been realized with photons with up to six particles and cold atoms of more than thousands of particles. They are highly entangled, and in quantum metrology they lead to the maximal Heisenberg scaling of the precision of parameter estimation. Defining equations Dicke states are defined in a system of N spin-s particles as the simultaneous eigenstates of the angular momentum operators ^2 and J_z by the equations : ^2, j,j_z,\alpha\rangle = j(j+1), j,j_z,\alpha\rangle and : J_z , j,j_z,\alpha\rangle = j_z, j,j_z,\alpha\rangle. Here, \alpha is a label used to distinguish several states orthogonal to each other, for which the two eigenvalues are the same. It i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
 |
Optical Cluster State
Optical cluster states are a proposed tool to achieve quantum computational universality in linear optical quantum computing (LOQC). As direct entangling operations with photons often require nonlinear effects, probabilistic generation of entangled resource states has been proposed as an alternative path to the direct approach. Creation of the cluster state On a silicon photonic chip, one of the most common platforms for implementing LOQC, there are two typical choices for encoding quantum information, though many more options exist. Photons have useful degrees of freedom in the spatial modes of the possible photon paths or in the polarization of the photons themselves. The way in which a cluster state is generated varies with which encoding has been chosen for implementation. Storing information in the spatial modes of the photon paths is often referred to as dual rail encoding. In a simple case, one might consider the situation where a photon has two possible paths, a horizonta ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
Graph State
In quantum computing, a graph state is a special type of multi-qubit state that can be represented by a graph. Each qubit is represented by a vertex of the graph, and there is an edge between every interacting pair of qubits. In particular, they are a convenient way of representing certain types of entangled states. Graph states are useful in quantum error-correcting codes, entanglement measurement and purification and for characterization of computational resources in measurement based quantum computing models. A graph state is a particular case of a stabilizer state as well as a 2-uniform hypergraph state, a generalization where the edges have cardinality between 1 and N. Formal definition Quantum graph states can be defined in two equivalent ways: through the notion of quantum circuits and stabilizer formalism. Quantum circuit definition Given a graph G = (V, E), with the set of vertices V and the set of edges E, the corresponding graph state is defined as : =\prod _ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Entanglement Witness
In quantum information theory, an entanglement witness is a functional which distinguishes a specific entangled state from separable ones. Entanglement witnesses can be linear or nonlinear functionals of the density matrix. If linear, then they can also be viewed as observables for which the expectation value of the entangled state is strictly outside the range of possible expectation values of any separable state. Details Let a composite quantum system have state space H_A \otimes H_B. A mixed state ''ρ'' is then a trace-class positive operator on the state space which has trace 1. We can view the family of states as a subset of the real Banach space generated by the Hermitian trace-class operators, with the trace norm. A mixed state ''ρ'' is separable if it can be approximated, in the trace norm, by states of the form :\xi = \sum_ ^k p_i \, \rho_i^A \otimes \rho_i^B, where \rho_i^A and \rho_i^B are pure states on the subsystems ''A'' and ''B'' respectively. So th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Fidelity Of Quantum States
In quantum mechanics, notably in quantum information theory, fidelity quantifies the "closeness" between two density matrices. It expresses the probability that one state will pass a test to identify as the other. It is not a metric on the space of density matrices, but it can be used to define the Bures metric on this space. Definition The fidelity between two quantum states ''\rho'' and ''\sigma'', expressed as density matrices, is commonly defined as:R. Jozsa, ''Fidelity for Mixed Quantum States'', J. Mod. Opt. 41, 2315--2323 (1994). DOI: http://doi.org/10.1080/09500349414552171 :F(\rho, \sigma) = \left(\operatorname \sqrt\right)^2. The square roots in this expression are well-defined because both \rho and \sqrt\rho\sigma\sqrt\rho are positive semidefinite matrices, and the square root of a positive semidefinite matrix is defined via the spectral theorem. The Euclidean inner product from the classical definition is replaced by the Hilbert–Schmidt inner product. As ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Ultracold Atom
In condensed matter physics, an ultracold atom is an atom with a temperature near absolute zero. At such temperatures, an atom's quantum-mechanical properties become important, especially through what's known as a "superfluid", such as Superfluid Helium 4. To reach such low temperatures, a combination of several techniques typically has to be used. First, atoms are trapped and pre-cooled via laser cooling in a magneto-optical trap. To reach the lowest possible temperature, further cooling is performed using evaporative cooling in a magnetic or optical trap. Several Nobel prizes in physics are related to the development of the techniques to manipulate quantum properties of individual atoms (e.g. 1989, 1996, 1997, 2001, 2005, 2012, 2018). Experiments with ultracold atoms study a variety of phenomena, including quantum phase transitions, Bose–Einstein condensation (BEC), bosonic superfluidity, quantum magnetism, many-body spin dynamics, Efimov states, Bardeen–Cooper� ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
 |
Optical Lattice
An optical lattice is formed by the Interference (wave propagation), interference of counter-propagating laser beams, creating a spatially periodic intensity pattern. The resulting periodic scalar potential, potential may trap neutral atoms via the Stark shift. Atoms are cooled and congregate at the potential extrema (at maxima for blue-detuned lattices, and minima for red-detuned lattices). The resulting arrangement of trapped atoms resembles a crystal lattice and can be used for Quantum simulator, quantum simulation. Atoms trapped in the optical lattice may move due to quantum tunneling, even if the potential well depth of the lattice points exceeds the kinetic energy of the atoms, which is similar to the electrons in a Electrical conductor, conductor. However, a superfluid–Mott insulator transition may occur, if the interaction energy between the atoms becomes larger than the hopping energy when the well depth is very large. In the Mott insulator phase, atoms will be trappe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
 |
Waveplate
A waveplate or retarder is an optics, optical device that alters the Polarization (waves), polarization state of a light wave travelling through it. Two common types of waveplates are the ''half-wave plate'', which rotates the polarization direction of linear polarization, linearly polarized light, and the ''quarter-wave plate'', which converts between different elliptical polarizations (such as the special case of converting from linearly polarized light to circular polarization, circularly polarized light and vice versa.) Waveplates are constructed out of a birefringence, birefringent material (such as quartz or mica, or even plastic), for which the index of refraction is different for light that is linearly polarized along one or the other of two certain perpendicular crystal axes. The behavior of a waveplate (that is, whether it is a half-wave plate, a quarter-wave plate, etc.) depends on the thickness of the crystal, the wavelength of light, and the variation of the index of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
Beam Splitter
A beam splitter or beamsplitter is an optical instrument, optical device that splits a beam of light into a transmitted and a reflected beam. It is a crucial part of many optical experimental and measurement systems, such as Interferometry, interferometers, also finding widespread application in fibre optic telecommunications. Designs In its most common form, a cube, a beam splitter is made from two triangular glass prism (optics), prisms which are glued together at their base using polyester, epoxy, or urethane-based adhesives. (Before these synthetic resins, natural ones were used, e.g. Canada balsam.) The thickness of the resin layer is adjusted such that (for a certain wavelength) half of the light incident through one "port" (i.e., face of the cube) is reflection (physics), reflected and the other half is transmitted due to Total internal reflection#Frustrated_TIR, FTIR (frustrated total internal reflection). polarizer, Polarizing beam splitters, such as the Wollaston prism ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
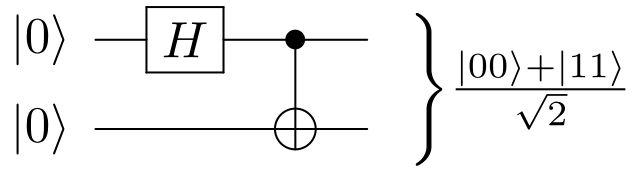 |
Bell State
In quantum information science, the Bell's states or EPR pairs are specific quantum states of two qubits that represent the simplest examples of quantum entanglement. The Bell's states are a form of entangled and normalized basis vectors. This normalization implies that the overall probability of the particles being in one of the mentioned states is 1: \langle \Phi, \Phi \rangle = 1. Entanglement is a basis-independent result of superposition. Due to this superposition, measurement of the qubit will " collapse" it into one of its basis states with a given probability. Because of the entanglement, measurement of one qubit will "collapse" the other qubit to a state whose measurement will yield one of two possible values, where the value depends on which Bell's state the two qubits are in initially. Bell's states can be generalized to certain quantum states of multi-qubit systems, such as the GHZ state for three or more subsystems. Understanding of Bell's states is useful in a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |