|
Degree (angle)
A degree (in full, a degree of arc, arc degree, or arcdegree), usually denoted by ° (the degree symbol), is a measurement of a plane (mathematics), plane angle in which one Turn (geometry), full rotation is 360 degrees. It is not an SI unit—the SI unit of angular measure is the radian—but it is mentioned in the SI Brochure, SI brochure as an Non-SI units mentioned in the SI, accepted unit. Because a full rotation equals 2 radians, one degree is equivalent to radians. History The original motivation for choosing the degree as a unit of rotations and angles is unknown. One theory states that it is related to the fact that 360 is approximately the number of days in a year. Ancient astronomers noticed that the sun, which follows through the ecliptic path over the course of the year, seems to advance in its path by approximately one degree each day. Some ancient calendars, such as the Iranian calendar, Persian calendar and the Babylonian calendar, used 360 days for a year. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Degree Diagram
Degree may refer to: As a unit of measurement * Degree (angle), a unit of angle measurement ** Degree of geographical latitude ** Degree of geographical longitude * Degree symbol (°), a notation used in science, engineering, and mathematics * Degree (temperature), any of various units of temperature measurement * Degree API, a measure of density in the petroleum industry * Degree Baumé, a pair of density scales * Degree Brix, a measure of sugar concentration * Degree Gay-Lussac, a measure of the alcohol content of a liquid by volume, ranging from 0° to 100° * Degree proof, or simply proof, the alcohol content of a liquid, ranging from 0° to 175° in the UK, and from 0° to 200° in the U.S. * Degree of curvature, a unit of curvature measurement, used in civil engineering * Degrees of freedom (mechanics), the number of displacements or rotations needed to define the position and orientation of a body * Degrees of freedom (physics and chemistry), a concept describing depende ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Astronomers
An astronomer is a scientist in the field of astronomy who focuses on a specific question or field outside the scope of Earth. Astronomers observe astronomical objects, such as stars, planets, moons, comets and galaxies – in either observational (by analyzing the data) or theoretical astronomy. Examples of topics or fields astronomers study include planetary science, solar astronomy, the origin or evolution of stars, or the formation of galaxies. A related but distinct subject is physical cosmology, which studies the Universe as a whole. Types Astronomers typically fall under either of two main types: observational and theoretical. Observational astronomers make direct observations of celestial objects and analyze the data. In contrast, theoretical astronomers create and investigate models of things that cannot be observed. Because it takes millions to billions of years for a system of stars or a galaxy to complete a life cycle, astronomers must observe snapshots o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
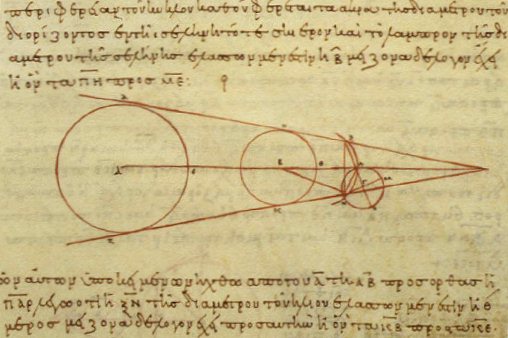
Hipparchus
Hipparchus (; , ; BC) was a Ancient Greek astronomy, Greek astronomer, geographer, and mathematician. He is considered the founder of trigonometry, but is most famous for his incidental discovery of the precession of the equinoxes. Hipparchus was born in Nicaea, Bithynia, and probably died on the island of Rhodes, Greece. He is known to have been a working astronomer between 162 and 127 BC. Hipparchus is considered the greatest ancient astronomical observer and, by some, the greatest overall astronomer of classical antiquity, antiquity. He was the first whose quantitative and accurate models for the motion of the Sun and Moon survive. For this he certainly made use of the observations and perhaps the mathematical techniques accumulated over centuries by the Babylonians and by Meton of Athens (fifth century BC), Timocharis, Aristyllus, Aristarchus of Samos, and Eratosthenes, among others. He developed trigonometry and constructed trigonometric tables, and he solved se ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Aristarchus Of Samos
Aristarchus of Samos (; , ; ) was an ancient Greek astronomer and mathematician who presented the first known heliocentric model that placed the Sun at the center of the universe, with the Earth revolving around the Sun once a year and rotating about its axis once a day. He also supported the theory of Anaxagoras according to which the Sun was just another star. He likely moved to Alexandria, and he was a student of Strato of Lampsacus, who later became the third head of the Peripatetic school in Greece. According to Ptolemy, he observed the summer solstice of 280 BC. Along with his contributions to the heliocentric model, as reported by Vitruvius, he created two separate sundials: one that is a flat disc; and one hemispherical. Aristarchus estimated the sizes of the Sun and Moon as compared to Earth's size. He also estimated the distances from the Earth to the Sun and Moon. His estimate that the Sun was 7 times larger than Earth (while inaccurate by an order of magnitu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chord (geometry)
A chord (from the Latin ''chorda'', meaning " bowstring") of a circle is a straight line segment whose endpoints both lie on a circular arc. If a chord were to be extended infinitely on both directions into a line, the object is a ''secant line''. The perpendicular line passing through the chord's midpoint is called '' sagitta'' (Latin for "arrow"). More generally, a chord is a line segment joining two points on any curve, for instance, on an ellipse. A chord that passes through a circle's center point is the circle's ''diameter''. In circles Among properties of chords of a circle are the following: # Chords are equidistant from the center if and only if their lengths are equal. # Equal chords are subtended by equal angles from the center of the circle. # A chord that passes through the center of a circle is called a diameter and is the longest chord of that specific circle. # If the line extensions (secant lines) of chords AB and CD intersect at a point P, then their ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Greek Astronomy
Ancient Greek astronomy is the astronomy written in the Greek language during classical antiquity. Greek astronomy is understood to include the Ancient Greece, Ancient Greek, Hellenistic period, Hellenistic, Roman Empire, Greco-Roman, and Late antiquity, late antique eras. Ancient Greek astronomy can be divided into three phases, with ''Classical Greek astronomy'' being practiced during the 5th and 4th centuries BC, ''Hellenistic period, Hellenistic astronomy'' from the 3rd century BC until the formation of the Roman Empire in the late 1st century BC, and ''Greco-Roman astronomy'' continuing the tradition in the Roman world. During the Hellenistic era and onwards, Greek astronomy expanded beyond the geographic region of Greece as the Greek language had become the language of scholarship throughout the Hellenistic world, in large part delimited by the boundaries of the Macedonian Empire established by Alexander the Great. The most prominent and influential practitione ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Babylonian Astronomy
Babylonian astronomy was the study or recording of celestial objects during the early history of Mesopotamia. The numeral system used, sexagesimal, was based on 60, as opposed to ten in the modern decimal system. This system simplified the calculating and recording of unusually great and small numbers. During the 8th and 7th centuries BC, Babylonian astronomers developed a new empirical approach to astronomy. They began studying and recording their belief system and philosophies dealing with an ideal nature of the universe and began employing an internal logic within their predictive planetary systems. This was an important contribution to astronomy and the philosophy of science, and some modern scholars have thus referred to this approach as a scientific revolution. This approach to astronomy was adopted and further developed in Greek and Hellenistic astrology. Classical Greek and Latin sources frequently use the term Chaldeans for the philosophers, who were cons ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
History Of Trigonometry
Early study of triangles can be traced to Egyptian mathematics (Rhind Mathematical Papyrus) and Babylonian mathematics during the 2nd millennium BC. Trigonometry was also prevalent in Kushite mathematics. Systematic study of trigonometric functions began in Hellenistic mathematics, reaching India as part of Hellenistic astronomy. In Indian astronomy, the study of trigonometric functions flourished in the Gupta period, especially due to Aryabhata (sixth century AD), who discovered the sine function, cosine function, and versine function. During the Middle Ages, the study of trigonometry continued in Islamic mathematics, by mathematicians such as al-Khwarizmi and Abu al-Wafa. The knowledge of trigonometric functions passed to Arabia from the Indian Subcontinent. It became an independent discipline in the Islamic world, where all six trigonometric functions were known. Translations of Arabic and Greek texts led to trigonometry being adopted as a subject in the Latin West beg ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cambridge University Press
Cambridge University Press was the university press of the University of Cambridge. Granted a letters patent by King Henry VIII in 1534, it was the oldest university press in the world. Cambridge University Press merged with Cambridge Assessment to form Cambridge University Press and Assessment under Queen Elizabeth II's approval in August 2021. With a global sales presence, publishing hubs, and offices in more than 40 countries, it published over 50,000 titles by authors from over 100 countries. Its publications include more than 420 academic journals, monographs, reference works, school and university textbooks, and English language teaching and learning publications. It also published Bibles, runs a bookshop in Cambridge, sells through Amazon, and has a conference venues business in Cambridge at the Pitt Building and the Sir Geoffrey Cass Sports and Social Centre. It also served as the King's Printer. Cambridge University Press, as part of the University of Cambridge, was a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equilateral Triangle
An equilateral triangle is a triangle in which all three sides have the same length, and all three angles are equal. Because of these properties, the equilateral triangle is a regular polygon, occasionally known as the regular triangle. It is the special case of an isosceles triangle by modern definition, creating more special properties. The equilateral triangle can be found in various tilings, and in polyhedrons such as the deltahedron and antiprism. It appears in real life in popular culture, architecture, and the study of stereochemistry resembling the molecular known as the trigonal planar molecular geometry. Properties An equilateral triangle is a triangle that has three equal sides. It is a special case of an isosceles triangle in the modern definition, stating that an isosceles triangle is defined at least as having two equal sides. Based on the modern definition, this leads to an equilateral triangle in which one of the three sides may be considered its base. Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sexagesimal
Sexagesimal, also known as base 60, is a numeral system with 60 (number), sixty as its radix, base. It originated with the ancient Sumerians in the 3rd millennium BC, was passed down to the ancient Babylonians, and is still used—in a modified form—for measuring time, angles, and geographic coordinate system, geographic coordinates. The number 60, a superior highly composite number, has twelve divisors, namely 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, and 60, of which 2, 3, and 5 are prime numbers. With so many factors, many fractions involving sexagesimal numbers are simplified. For example, one hour can be divided evenly into sections of 30 minutes, 20 minutes, 15 minutes, 12 minutes, 10 minutes, 6 minutes, 5 minutes, 4 minutes, 3 minutes, 2 minutes, and 1 minute. 60 is the smallest number that is divisible by every number from 1 to 6; that is, it is the lowest common multiple of 1, 2, 3, 4, 5, and 6. ''In this article, all sexagesimal digits are represented as decimal numbers, e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Babylonian Calendar
The Babylonian calendar was a lunisolar calendar used in Mesopotamia from around the 2nd millennium BC until the Seleucid Era ( 294 BC), and it was specifically used in Babylon from the Old Babylonian Period ( 1780s BC) until the Seleucid Era. In the Seleucid Era it was reformed as "Greek time", Anno Graecorum was introduced and used in the Middle East and Egypt until the middle of the first millennium when the First Council of Nicaea AD 325 defined the Church year based on the Roman early Julian calendar. As Anno Graecorum formed the basis for time references in the Bible and spread westward, it rather increased the Babylonian calendars importance. The Babylonian calendar is also partly reflected in calendars in South and East Asia and the Islamic calendar as well as Iranian calendars. The Julian calendar inherited the definitions of the 12 month system, week, hour etc. from the Babylonian calendar and the current Jewish calendar can be seen as a slightly modified Baby ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |