|
Conservative Force
In physics, a conservative force is a force with the property that the total work done by the force in moving a particle between two points is independent of the path taken. Equivalently, if a particle travels in a closed loop, the total work done (the sum of the force acting along the path multiplied by the displacement) by a conservative force is zero. A conservative force depends only on the position of the object. If a force is conservative, it is possible to assign a numerical value for the potential at any point and conversely, when an object moves from one location to another, the force changes the potential energy of the object by an amount that does not depend on the path taken, contributing to the mechanical energy and the overall conservation of energy. If the force is not conservative, then defining a scalar potential is not possible, because taking different paths would lead to conflicting potential differences between the start and end points. Gravitational for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Physics
Physics is the scientific study of matter, its Elementary particle, fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge which relates to the order of nature, or, in other words, to the regular succession of events." It is one of the most fundamental scientific disciplines. "Physics is one of the most fundamental of the sciences. Scientists of all disciplines use the ideas of physics, including chemists who study the structure of molecules, paleontologists who try to reconstruct how dinosaurs walked, and climatologists who study how human activities affect the atmosphere and oceans. Physics is also the foundation of all engineering and technology. No engineer could design a flat-screen TV, an interplanetary spacecraft, or even a better mousetrap without first understanding the basic laws of physics. (...) You will come to see physics as a towering achievement of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Friction
Friction is the force resisting the relative motion of solid surfaces, fluid layers, and material elements sliding against each other. Types of friction include dry, fluid, lubricated, skin, and internal -- an incomplete list. The study of the processes involved is called tribology, and has a history of more than 2000 years. Friction can have dramatic consequences, as illustrated by the use of friction created by rubbing pieces of wood together to start a fire. Another important consequence of many types of friction can be wear, which may lead to performance degradation or damage to components. It is known that frictional energy losses account for about 20% of the total energy expenditure of the world. As briefly discussed later, there are many different contributors to the retarding force in friction, ranging from asperity deformation to the generation of charges and changes in local structure. When two bodies in contact move relative to each other, due to these variou ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Gradient
In vector calculus, the gradient of a scalar-valued differentiable function f of several variables is the vector field (or vector-valued function) \nabla f whose value at a point p gives the direction and the rate of fastest increase. The gradient transforms like a vector under change of basis of the space of variables of f. If the gradient of a function is non-zero at a point p, the direction of the gradient is the direction in which the function increases most quickly from p, and the magnitude of the gradient is the rate of increase in that direction, the greatest absolute directional derivative. Further, a point where the gradient is the zero vector is known as a stationary point. The gradient thus plays a fundamental role in optimization theory, where it is used to minimize a function by gradient descent. In coordinate-free terms, the gradient of a function f(\mathbf) may be defined by: df=\nabla f \cdot d\mathbf where df is the total infinitesimal change in f for a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Work (physics)
In science, work is the energy transferred to or from an Physical object, object via the application of force along a Displacement (vector), displacement. In its simplest form, for a constant force aligned with the direction of motion, the work equals the Product (mathematics), product of the force strength and the distance traveled. A force is said to do ''positive work'' if it has a component in the direction of the displacement of the point of application. A force does ''negative work'' if it has a component opposite to the direction of the displacement at the point of application of the force. For example, when a ball is held above the ground and then dropped, the work done by the gravitational force on the ball as it falls is positive, and is equal to the weight of the ball (a force) multiplied by the distance to the ground (a displacement). If the ball is thrown upwards, the work done by the gravitational force is negative, and is equal to the weight multiplied by the dis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Curl (mathematics)
In vector calculus, the curl, also known as rotor, is a vector operator that describes the Differential (infinitesimal), infinitesimal Circulation (physics), circulation of a vector field in three-dimensional Euclidean space. The curl at a point in the field is represented by a vector (geometry), vector whose length and direction denote the Magnitude (mathematics), magnitude and axis of the maximum circulation. The curl of a field is formally defined as the circulation density at each point of the field. A vector field whose curl is zero is called irrotational. The curl is a form of derivative, differentiation for vector fields. The corresponding form of the fundamental theorem of calculus is Kelvin–Stokes theorem, Stokes' theorem, which relates the surface integral of the curl of a vector field to the line integral of the vector field around the boundary curve. The notation is more common in North America. In the rest of the world, particularly in 20th century scientific li ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Conservative Vector Field
In vector calculus, a conservative vector field is a vector field that is the gradient of some function. A conservative vector field has the property that its line integral is path independent; the choice of path between two points does not change the value of the line integral. Path independence of the line integral is equivalent to the vector field under the line integral being conservative. A conservative vector field is also irrotational; in three dimensions, this means that it has vanishing curl. An irrotational vector field is necessarily conservative provided that the domain is simply connected. Conservative vector fields appear naturally in mechanics: They are vector fields representing forces of physical systems in which energy is conserved. For a conservative system, the work done in moving along a path in a configuration space depends on only the endpoints of the path, so it is possible to define potential energy that is independent of the actual path taken. Inform ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Simply-connected
In topology, a topological space is called simply connected (or 1-connected, or 1-simply connected) if it is path-connected and every path between two points can be continuously transformed into any other such path while preserving the two endpoints in question. Intuitively, this corresponds to a space that has no disjoint parts and no holes that go completely through it, because two paths going around different sides of such a hole cannot be continuously transformed into each other. The fundamental group of a topological space is an indicator of the failure for the space to be simply connected: a path-connected topological space is simply connected if and only if its fundamental group is trivial. Definition and equivalent formulations A topological space X is called if it is path-connected and any loop in X defined by f : S^1 \to X can be contracted to a point: there exists a continuous map F : D^2 \to X such that F restricted to S^1 is f. Here, S^1 and D^2 denotes the unit circ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Force Field (physics)
In physics, a force field is a vector field corresponding with a non-contact force acting on a particle at various positions in space. Specifically, a force field is a vector field \mathbf F, where \mathbf F(\mathbf r) is the force that a particle would feel if it were at the position \mathbf r. Examples *Gravity is the force of attraction between two objects. A gravitational force field models this influence that a massive body (or more generally, any quantity of energy) extends into the space around itself. In Newtonian gravity, a particle of mass ''M'' creates a gravitational field \mathbf g=\frac\hat\mathbf r, where the radial unit vector \hat\mathbf r points away from the particle. The gravitational force experienced by a particle of light mass ''m'', close to the surface of Earth is given by \mathbf F = m \mathbf g, where ''g'' is Earth's gravity. *An electric field \mathbf E exerts a force on a point charge ''q'', given by \mathbf F = q\mathbf E. *In a magnetic field \m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Conservative Force Gravity Example
Conservatism is a cultural, social, and political philosophy and ideology that seeks to promote and preserve traditional institutions, customs, and values. The central tenets of conservatism may vary in relation to the culture and civilization in which it appears. In Western culture, depending on the particular nation, conservatives seek to promote and preserve a range of institutions, such as the nuclear family, organized religion, the military, the nation-state, property rights, rule of law, aristocracy, and monarchy. Conservatives tend to favor institutions and practices that enhance social order and historical continuity. The 18th-century Anglo-Irish statesman Edmund Burke, who opposed the French Revolution but supported the American Revolution, is credited as one of the forefathers of conservative thought in the 1790s along with Savoyard statesman Joseph de Maistre. The first established use of the term in a political context originated in 1818 with François-René de C ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
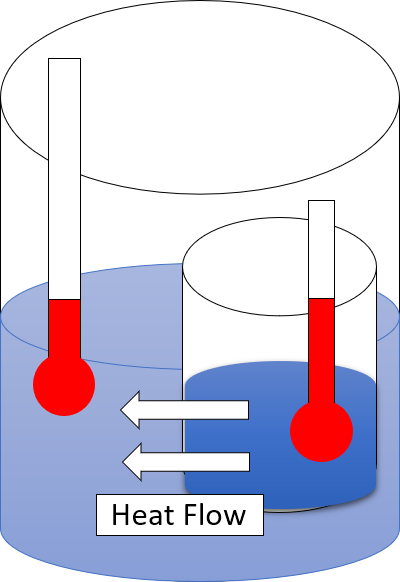
Second Law Of Thermodynamics
The second law of thermodynamics is a physical law based on Universal (metaphysics), universal empirical observation concerning heat and Energy transformation, energy interconversions. A simple statement of the law is that heat always flows spontaneously from hotter to colder regions of matter (or 'downhill' in terms of the temperature gradient). Another statement is: "Not all heat can be converted into Work (thermodynamics), work in a cyclic process."Young, H. D; Freedman, R. A. (2004). ''University Physics'', 11th edition. Pearson. p. 764. The second law of thermodynamics establishes the concept of entropy as a physical property of a thermodynamic system. It predicts whether processes are forbidden despite obeying the requirement of conservation of energy as expressed in the first law of thermodynamics and provides necessary criteria for spontaneous processes. For example, the first law allows the process of a cup falling off a table and breaking on the floor, as well as allowi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Wake (physics)
In fluid dynamics, a wake may either be: * the region of recirculating flow immediately behind a moving or stationary blunt body, caused by viscosity, which may be accompanied by flow separation and turbulence, or * the wave pattern on the water surface downstream of an object in a flow, or produced by a moving object (e.g. a ship), caused by density differences of the fluids above and below the free surface and gravity (or surface tension). Viscosity The wake is the region of disturbed flow (often turbulent) downstream of a solid body moving through a fluid, caused by the flow of the fluid around the body. For a blunt body in subsonic external flow, for example the Apollo or Orion capsules during descent and landing, the wake is massively separated and behind the body is a reverse flow region where the flow is moving toward the body. This phenomenon is often observed in wind tunnel testing of aircraft, and is especially important when parachute systems are involved, becaus ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Sound Energy
In physics, sound energy is a form of energy that can be heard by living things. Only those waves that have a frequency of 20 Hz to 20 kHz are audible to humans. However, this range is an average and will slightly change from individual to individual. Sound waves that have frequencies below 20 Hz are called infrasonic and those above 20 kHz are called ultrasonic. Sound is a longitudinal mechanical wave and as such consists physically in oscillatory elastic compression and in oscillatory displacement of a fluid. Therefore, the medium acts as storage for both potential and kinetic energy. Consequently, the sound energy in a volume of interest is defined as the sum of the potential and kinetic energy densities integrated over that volume: :W = W_\mathrm + W_\mathrm = \int_V \frac\, \mathrmV + \int_V \frac\, \mathrmV, where *''V'' is the volume of interest; *''p'' is the sound pressure; *''v'' is the particle velocity; *''ρ''0 is the density of the medium wit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |