|
Corner Detection
Corner detection is an approach used within computer vision systems to extract certain kinds of Feature detection (computer vision), features and infer the contents of an image. Corner detection is frequently used in motion detection, image registration, video tracking, photographic mosaic, image mosaicing, panorama stitching, 3D reconstruction and object recognition. Corner detection overlaps with the topic of interest point detection. Formalization A corner can be defined as the intersection of two edges. A corner can also be defined as a point for which there are two dominant and different edge directions in a local neighbourhood of the point. An interest point is a point in an image which has a well-defined position and can be robustly detected. This means that an interest point can be a corner but it can also be, for example, an isolated point of local intensity maximum or minimum, line endings, or a point on a curve where the curvature is locally maximal. In practice, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Corner
Corner may refer to: People *Corner (surname) *House of Cornaro, a noble Venetian family (''Corner'' in Venetian dialect) Places * Corner, Alabama, a community in the United States *Corner Inlet, Victoria, Australia * Corner River, a tributary of Harricana River, in Ontario, Canada * Corner Township, Custer County, Nebraska, a township in the United States Arts, entertainment, and media Music * ''The Corner'' (album), an album by the Hieroglyphics * "The Corner" (song), a 2005 song by Common * "Corner", a song by Allie Moss from her 2009 EP ''Passerby'' * "Corner", a song by Blue Stahli from their 2010 album ''Blue Stahli'' * "The Corner", a song by Dermot Kennedy from his 2019 album '' Without Fear'' * "The Corner", a song by Rodney Atkins from his 2011 album ''Take a Back Road'' * "The Corner", a song by Staind from their 2008 album '' The Illusion of Progress'' Other uses in arts, entertainment, and media * Corner painters, a Danish artists association * ''The Corner'' (191 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isotropic
In physics and geometry, isotropy () is uniformity in all orientations. Precise definitions depend on the subject area. Exceptions, or inequalities, are frequently indicated by the prefix ' or ', hence '' anisotropy''. ''Anisotropy'' is also used to describe situations where properties vary systematically, dependent on direction. Isotropic radiation has the same intensity regardless of the direction of measurement, and an isotropic field exerts the same action regardless of how the test particle is oriented. Mathematics Within mathematics, ''isotropy'' has a few different meanings: ; Isotropic manifolds: A manifold is isotropic if the geometry on the manifold is the same regardless of direction. A similar concept is homogeneity. ; Isotropic quadratic form: A quadratic form ''q'' is said to be isotropic if there is a non-zero vector ''v'' such that ; such a ''v'' is an isotropic vector or null vector. In complex geometry, a line through the origin in the direction of an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Harmonic Mean
In mathematics, the harmonic mean is a kind of average, one of the Pythagorean means. It is the most appropriate average for ratios and rate (mathematics), rates such as speeds, and is normally only used for positive arguments. The harmonic mean is the multiplicative inverse, reciprocal of the arithmetic mean of the reciprocals of the numbers, that is, the generalized f-mean with f(x) = \frac. For example, the harmonic mean of 1, 4, and 4 is :\left(\frac\right)^ = \frac = \frac = 2\,. Definition The harmonic mean ''H'' of the positive real numbers x_1, x_2, \ldots, x_n is :H(x_1, x_2, \ldots, x_n) = \frac = \frac. It is the reciprocal of the arithmetic mean of the reciprocals, and vice versa: :\begin H(x_1, x_2, \ldots, x_n) &= \frac, \\ A(x_1, x_2, \ldots, x_n) &= \frac, \end where the arithmetic mean is A(x_1, x_2, \ldots, x_n) = \tfrac1n \sum_^n x_i. The harmonic mean is a Schur-concave function, and is greater than or equal to the minimum of its arguments: for positive a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trace (linear Algebra)
In linear algebra, the trace of a square matrix , denoted , is the sum of the elements on its main diagonal, a_ + a_ + \dots + a_. It is only defined for a square matrix (). The trace of a matrix is the sum of its eigenvalues (counted with multiplicities). Also, for any matrices and of the same size. Thus, similar matrices have the same trace. As a consequence, one can define the trace of a linear operator mapping a finite-dimensional vector space into itself, since all matrices describing such an operator with respect to a basis are similar. The trace is related to the derivative of the determinant (see Jacobi's formula). Definition The trace of an square matrix is defined as \operatorname(\mathbf) = \sum_^n a_ = a_ + a_ + \dots + a_ where denotes the entry on the row and column of . The entries of can be real numbers, complex numbers, or more generally elements of a field . The trace is not defined for non-square matrices. Example Let be a matrix, with \m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Determinant
In mathematics, the determinant is a Scalar (mathematics), scalar-valued function (mathematics), function of the entries of a square matrix. The determinant of a matrix is commonly denoted , , or . Its value characterizes some properties of the matrix and the linear map represented, on a given basis (linear algebra), basis, by the matrix. In particular, the determinant is nonzero if and only if the matrix is invertible matrix, invertible and the corresponding linear map is an linear isomorphism, isomorphism. However, if the determinant is zero, the matrix is referred to as singular, meaning it does not have an inverse. The determinant is completely determined by the two following properties: the determinant of a product of matrices is the product of their determinants, and the determinant of a triangular matrix is the product of its diagonal entries. The determinant of a matrix is :\begin a & b\\c & d \end=ad-bc, and the determinant of a matrix is : \begin a & b & c \\ d & e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eigenvalue Decomposition
In linear algebra, eigendecomposition is the factorization of a matrix into a canonical form, whereby the matrix is represented in terms of its eigenvalues and eigenvectors. Only diagonalizable matrices can be factorized in this way. When the matrix being factorized is a normal or real symmetric matrix, the decomposition is called "spectral decomposition", derived from the spectral theorem. Fundamental theory of matrix eigenvectors and eigenvalues A (nonzero) vector of dimension is an eigenvector of a square matrix if it satisfies a linear equation of the form \mathbf \mathbf = \lambda \mathbf for some scalar . Then is called the eigenvalue corresponding to . Geometrically speaking, the eigenvectors of are the vectors that merely elongates or shrinks, and the amount that they elongate/shrink by is the eigenvalue. The above equation is called the eigenvalue equation or the eigenvalue problem. This yields an equation for the eigenvalues p\left(\lambda\right) = \det\lef ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Square Root
In mathematics, a square root of a number is a number such that y^2 = x; in other words, a number whose ''square'' (the result of multiplying the number by itself, or y \cdot y) is . For example, 4 and −4 are square roots of 16 because 4^2 = (-4)^2 = 16. Every nonnegative real number has a unique nonnegative square root, called the ''principal square root'' or simply ''the square root'' (with a definite article, see below), which is denoted by \sqrt, where the symbol "\sqrt" is called the '' radical sign'' or ''radix''. For example, to express the fact that the principal square root of 9 is 3, we write \sqrt = 3. The term (or number) whose square root is being considered is known as the ''radicand''. The radicand is the number or expression underneath the radical sign, in this case, 9. For non-negative , the principal square root can also be written in exponent notation, as x^. Every positive number has two square roots: \sqrt (which is positive) and -\sqrt (which i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
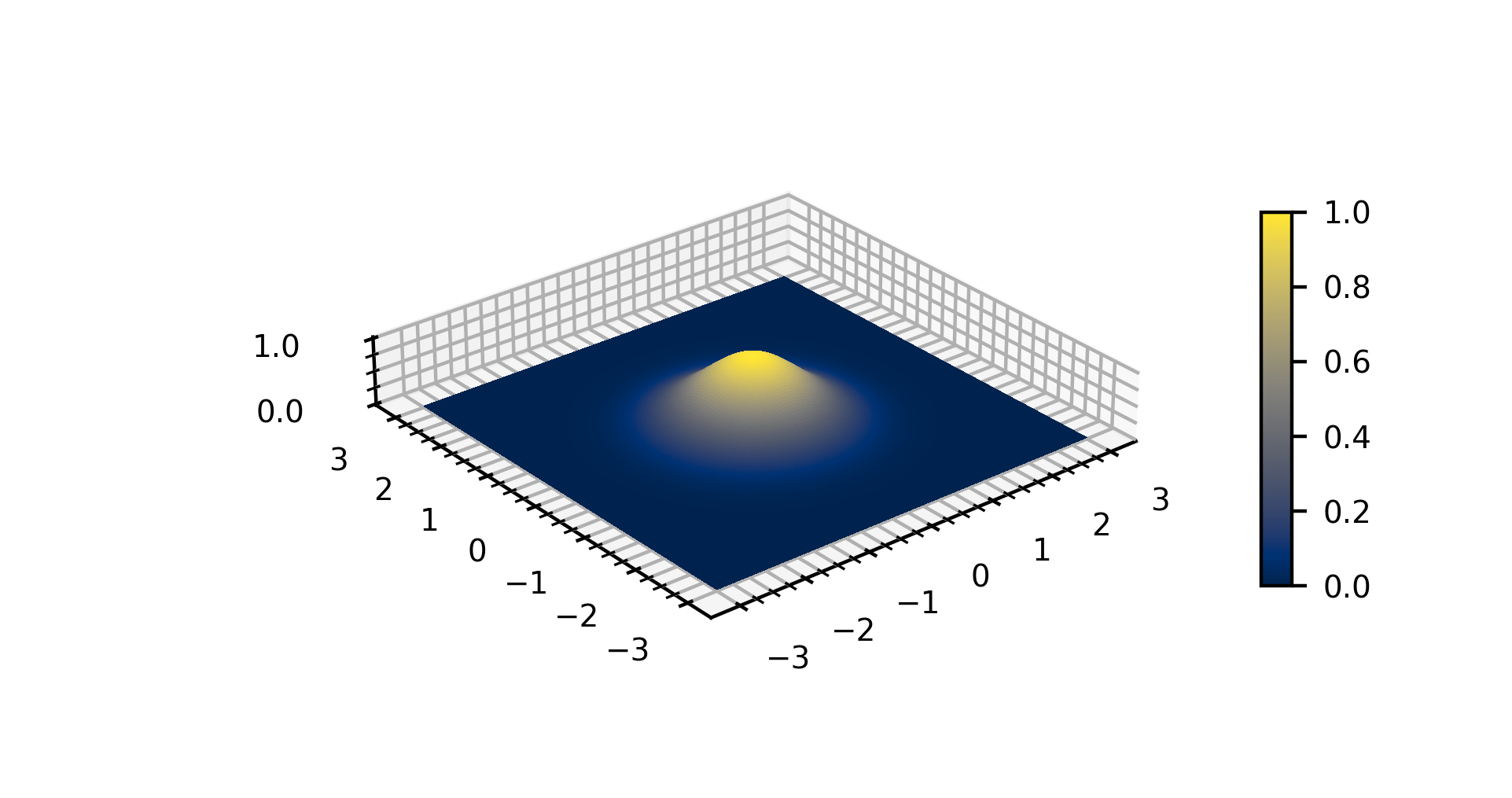
Gaussian Function
In mathematics, a Gaussian function, often simply referred to as a Gaussian, is a function (mathematics), function of the base form f(x) = \exp (-x^2) and with parametric extension f(x) = a \exp\left( -\frac \right) for arbitrary real number, real constants , and non-zero . It is named after the mathematician Carl Friedrich Gauss. The graph of a function, graph of a Gaussian is a characteristic symmetric "Normal distribution, bell curve" shape. The parameter is the height of the curve's peak, is the position of the center of the peak, and (the standard deviation, sometimes called the Gaussian Root mean square, RMS width) controls the width of the "bell". Gaussian functions are often used to represent the probability density function of a normal distribution, normally distributed random variable with expected value and variance . In this case, the Gaussian is of the form g(x) = \frac \exp\left( -\frac \frac \right). Gaussian functions are widely used in statistics to describ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Anisotropy
Anisotropy () is the structural property of non-uniformity in different directions, as opposed to isotropy. An anisotropic object or pattern has properties that differ according to direction of measurement. For example, many materials exhibit very different physical or mechanical properties when measured along different axes, e.g. absorbance, refractive index, conductivity, and tensile strength. An example of anisotropy is light coming through a polarizer. Another is wood, which is easier to split along its grain than across it because of the directional non-uniformity of the grain (the grain is the same in one direction, not all directions). Fields of interest Computer graphics In the field of computer graphics, an anisotropic surface changes in appearance as it rotates about its geometric normal, as is the case with velvet. Anisotropic filtering (AF) is a method of enhancing the image quality of textures on surfaces that are far away and viewed at a shallow angle. Older ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Box Blur
A box blur (also known as a box linear filter) is a spatial domain linear filter in which each pixel in the resulting image has a value equal to the average value of its neighboring pixels in the input image. It is a form of low-pass ("blurring") filter. A 3 by 3 box blur ("radius 1") can be written as matrix :\frac\begin 1 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \end. Due to its property of using equal weights, it can be implemented using a much simpler accumulation algorithm, which is significantly faster than using a sliding-window algorithm. Box blurs are frequently used to approximate a Gaussian blur. By the central limit theorem, repeated application of a box blur will approximate a Gaussian blur.code doc In the frequency domain, a box blur has zeros and negative components. That is, a sine wave with a period equal to the size of the box will be blurred away entirely, and wavelengths shorter than the size of the box may be phase-reversed, as seen when two bokeh circles touch to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Covariance
In probability theory and statistics, covariance is a measure of the joint variability of two random variables. The sign of the covariance, therefore, shows the tendency in the linear relationship between the variables. If greater values of one variable mainly correspond with greater values of the other variable, and the same holds for lesser values (that is, the variables tend to show similar behavior), the covariance is positive. In the opposite case, when greater values of one variable mainly correspond to lesser values of the other (that is, the variables tend to show opposite behavior), the covariance is negative. The magnitude of the covariance is the geometric mean of the variances that are in common for the two random variables. The Pearson product-moment correlation coefficient, correlation coefficient normalizes the covariance by dividing by the geometric mean of the total variances for the two random variables. A distinction must be made between (1) the covariance of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Structure Tensor
In mathematics, the structure tensor, also referred to as the second-moment matrix, is a matrix (mathematics), matrix derived from the gradient of a function (mathematics), function. It describes the distribution of the gradient in a specified neighborhood around a point and makes the information invariant to the observing coordinates. The structure tensor is often used in image processing and computer vision. J. Bigun and G. Granlund (1986), ''Optimal Orientation Detection of Linear Symmetry''. Tech. Report LiTH-ISY-I-0828, Computer Vision Laboratory, Linkoping University, Sweden 1986; Thesis Report, Linkoping studies in science and technology No. 85, 1986. The 2D structure tensor Continuous version For a function I of two variables , the structure tensor is the 2×2 matrix S_w(p) = \begin \int w(r) (I_x(p-r))^2\,dr & \int w(r) I_x(p-r)I_y(p-r)\,dr \\[10pt] \int w(r) I_x(p-r)I_y(p-r)\,dr & \int w(r) (I_y(p-r))^2\,dr \end where I_x and I_y are the partial derivatives of I ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |