|
Compact Manifold
In mathematics, a closed manifold is a manifold Manifold with boundary, without boundary that is Compact space, compact. In comparison, an open manifold is a manifold without boundary that has only ''non-compact'' components. Examples The only Connected space, connected one-dimensional example is a circle. The sphere, torus, and the Klein bottle are all closed two-dimensional manifolds. The real projective space RP''n'' is a closed ''n''-dimensional manifold. The complex projective space CP''n'' is a closed 2''n''-dimensional manifold. A Real line, line is not closed because it is not compact. A closed disk is a compact two-dimensional manifold, but it is not closed because it has a boundary. Properties Every closed manifold is a Euclidean neighborhood retract and thus has finitely generated homology groups. If M is a closed connected n-manifold, the n-th homology group H_(M;\mathbb) is \mathbb or 0 depending on whether M is Orientability, orientable or not. Moreover, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Universal Coefficient Theorem
In algebraic topology, universal coefficient theorems establish relationships between homology groups (or cohomology groups) with different coefficients. For instance, for every topological space , its ''integral homology groups'': :H_i(X,\Z) completely determine its ''homology groups with coefficients in'' , for any abelian group : :H_i(X,A) Here H_i might be the simplicial homology, or more generally the singular homology. The usual proof of this result is a pure piece of homological algebra about chain complexes of free abelian groups. The form of the result is that other coefficients may be used, at the cost of using a Tor functor. For example, it is common to take A to be \Z/2\Z, so that coefficients are modulo 2. This becomes straightforward in the absence of 2- torsion in the homology. Quite generally, the result indicates the relationship that holds between the Betti numbers b_i of X and the Betti numbers b_ with coefficients in a field F. These can differ, but o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Differential Geometry
Differential geometry is a Mathematics, mathematical discipline that studies the geometry of smooth shapes and smooth spaces, otherwise known as smooth manifolds. It uses the techniques of Calculus, single variable calculus, vector calculus, linear algebra and multilinear algebra. The field has its origins in the study of spherical geometry as far back as classical antiquity, antiquity. It also relates to astronomy, the geodesy of the Earth, and later the study of hyperbolic geometry by Nikolai Lobachevsky, Lobachevsky. The simplest examples of smooth spaces are the Differential geometry of curves, plane and space curves and Differential geometry of surfaces, surfaces in the three-dimensional Euclidean space, and the study of these shapes formed the basis for development of modern differential geometry during the 18th and 19th centuries. Since the late 19th century, differential geometry has grown into a field concerned more generally with geometric structures on differentiable ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Allen Hatcher
Allen Edward Hatcher (born October 23, 1944) is an American mathematician specializing in geometric topology. Biography Hatcher was born in Indianapolis, Indiana. After obtaining his Bachelor of Arts, B.A. and Bachelor of Music, B.Mus. from Oberlin College in 1966, he went for his graduate studies to Stanford University, where he received his Doctor of Philosophy, Ph.D. in 1971. His thesis, ''A K2 Obstruction for Pseudo-Isotopies'', was written under the supervision of Hans Samelson. Afterwards, Hatcher went to Princeton University, where he was an National Science Foundation, NSF postdoc for a year, then a lecturer for another year, and then Assistant Professor from 1973 to 1979. He was also a member of the Institute for Advanced Study in 1975–76 and 1979–80. Hatcher moved to the University of California, Los Angeles as an assistant professor in 1977. From 1983 he has been a professor at Cornell University; he is now a emeritus, professor emeritus. In 1978 Hatcher was an Li ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Michael Spivak
Michael David Spivak (May 25, 1940October 1, 2020) was an American mathematician specializing in differential geometry, an expositor of mathematics, and the founder of Publish-or-Perish Press. Spivak was the author of the five-volume ''A Comprehensive Introduction to Differential Geometry'', which won the Leroy P. Steele Prize for expository writing in 1985. Biography Spivak was born in Queens, New York. He received his Bachelor of Arts (A.B.) from Harvard University in 1960, and in 1964 he received his Ph.D. from Princeton University under the supervision of John Milnor, with his thesis, ''On Spaces Satisfying Poincaré Duality''. Afterwards, Spivak taught as a full-time Math Lecturer at Brandeis University, whilst writing '' Calculus on Manifolds: A Modern Approach to Classical Theorems of Advanced Calculus'', which was later translated into Polish, Spanish, Japanese and Russian. In 1967, he won a year-long National Science Foundation fellowship to Princeton’s Institute fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ricci Curvature
In differential geometry, the Ricci curvature tensor, named after Gregorio Ricci-Curbastro, is a geometric object which is determined by a choice of Riemannian or pseudo-Riemannian metric on a manifold. It can be considered, broadly, as a measure of the degree to which the geometry of a given metric tensor differs locally from that of ordinary Euclidean space or pseudo-Euclidean space. The Ricci tensor can be characterized by measurement of how a shape is deformed as one moves along geodesics in the space. In general relativity, which involves the pseudo-Riemannian setting, this is reflected by the presence of the Ricci tensor in the Raychaudhuri equation. Partly for this reason, the Einstein field equations propose that spacetime can be described by a pseudo-Riemannian metric, with a strikingly simple relationship between the Ricci tensor and the matter content of the universe. Like the metric tensor, the Ricci tensor assigns to each tangent space of the manifold a symmetric bi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
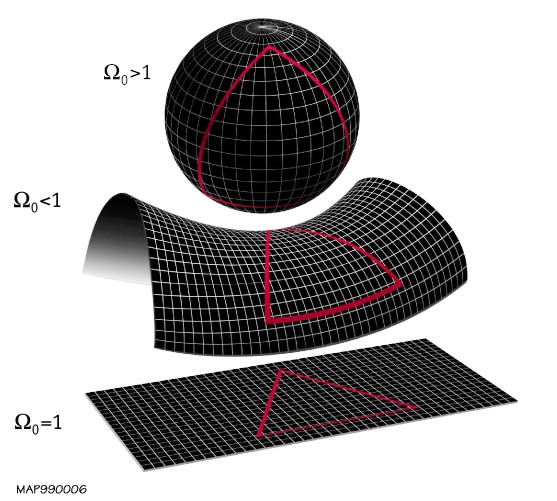
Shape Of The Universe
In physical cosmology, the shape of the universe refers to both its local and global geometry. Local geometry is defined primarily by its curvature, while the global geometry is characterised by its topology (which itself is constrained by curvature). General relativity explains how spatial curvature (local geometry) is constrained by gravity. The global topology of the universe cannot be deduced from measurements of curvature inferred from observations within the family of homogeneous general relativistic models alone, due to the existence of locally indistinguishable spaces with varying global topological characteristics. For example; a multiply connected space like a 3 torus has everywhere zero curvature but is finite in extent, whereas a flat simply connected space is infinite in extent (such as Euclidean space). Current observational evidence ( WMAP, BOOMERanG, and Planck for example) imply that the observable universe is spatially flat to within a 0.4% margin of error o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Closed Set
In geometry, topology, and related branches of mathematics, a closed set is a Set (mathematics), set whose complement (set theory), complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points. In a complete metric space, a closed set is a set which is Closure (mathematics), closed under the limit of a sequence, limit operation. This should not be confused with closed manifold. Sets that are both open and closed and are called clopen sets. Definition Given a topological space (X, \tau), the following statements are equivalent: # a set A \subseteq X is in X. # A^c = X \setminus A is an open subset of (X, \tau); that is, A^ \in \tau. # A is equal to its Closure (topology), closure in X. # A contains all of its limit points. # A contains all of its Boundary (topology), boundary points. An alternative characterization (mathematics), characterization of closed sets is available via sequences and Net (mathematics), net ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Manifold With Boundary
In mathematics, a manifold is a topological space that locally resembles Euclidean space near each point. More precisely, an n-dimensional manifold, or ''n-manifold'' for short, is a topological space with the property that each point has a neighborhood that is homeomorphic to an open subset of n-dimensional Euclidean space. One-dimensional manifolds include lines and circles, but not self-crossing curves such as a figure 8. Two-dimensional manifolds are also called surfaces. Examples include the plane, the sphere, and the torus, and also the Klein bottle and real projective plane. The concept of a manifold is central to many parts of geometry and modern mathematical physics because it allows complicated structures to be described in terms of well-understood topological properties of simpler spaces. Manifolds naturally arise as solution sets of systems of equations and as graphs of functions. The concept has applications in computer-graphics given the need to associate ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclidean Space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are ''Euclidean spaces'' of any positive integer dimension ''n'', which are called Euclidean ''n''-spaces when one wants to specify their dimension. For ''n'' equal to one or two, they are commonly called respectively Euclidean lines and Euclidean planes. The qualifier "Euclidean" is used to distinguish Euclidean spaces from other spaces that were later considered in physics and modern mathematics. Ancient Greek geometers introduced Euclidean space for modeling the physical space. Their work was collected by the ancient Greek mathematician Euclid in his ''Elements'', with the great innovation of '' proving'' all properties of the space as theorems, by starting from a few fundamental properties, called '' postulates'', which either were considered as evid ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Homeomorphic
In mathematics and more specifically in topology, a homeomorphism ( from Greek roots meaning "similar shape", named by Henri Poincaré), also called topological isomorphism, or bicontinuous function, is a bijective and continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are the mappings that preserve all the topological properties of a given space. Two spaces with a homeomorphism between them are called homeomorphic, and from a topological viewpoint they are the same. Very roughly speaking, a topological space is a geometric object, and a homeomorphism results from a continuous deformation of the object into a new shape. Thus, a square and a circle are homeomorphic to each other, but a sphere and a torus are not. However, this description can be misleading. Some continuous deformations do not produce homeomorphisms, such as the deformation of a li ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Poincaré Duality
In mathematics, the Poincaré duality theorem, named after Henri Poincaré, is a basic result on the structure of the homology (mathematics), homology and cohomology group (mathematics), groups of manifolds. It states that if ''M'' is an ''n''-dimensional Orientability, oriented closed manifold (Compact space, compact and without boundary), then the ''k''th cohomology group of ''M'' is Group isomorphism, isomorphic to the th homology group of ''M'', for all integers ''k'' : H^k(M) \cong H_(M). Poincaré duality holds for any coefficient ring (mathematics), ring, so long as one has taken an orientation with respect to that coefficient ring; in particular, since every manifold has a unique orientation mod 2, Poincaré duality holds mod 2 without any assumption of orientation. History A form of Poincaré duality was first stated, without proof, by Henri Poincaré in 1893. It was stated in terms of Betti numbers: The ''k''th and th Betti numbers of a closed (i.e., compact and witho ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |