|
Chomsky Normal Form
In formal language theory, a context-free grammar, ''G'', is said to be in Chomsky normal form (first described by Noam Chomsky) if all of its production rules are of the form: : ''A'' → ''BC'', or : ''A'' → ''a'', or : ''S'' → ε, where ''A'', ''B'', and ''C'' are nonterminal symbols, the letter ''a'' is a terminal symbol (a symbol that represents a constant value), ''S'' is the start symbol, and ε denotes the empty string. Also, neither ''B'' nor ''C'' may be the start symbol, and the third production rule can only appear if ε is in ''L''(''G''), the language produced by the context-free grammar ''G''. Every grammar in Chomsky normal form is context-free, and conversely, every context-free grammar can be transformed into an equivalent onethat is, one that produces the same language which is in Chomsky normal form and has a size no larger than the square of the original grammar's size. Converting a grammar to Chomsky normal form To convert a grammar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Formal Language
In logic, mathematics, computer science, and linguistics, a formal language is a set of strings whose symbols are taken from a set called "alphabet". The alphabet of a formal language consists of symbols that concatenate into strings (also called "words"). Words that belong to a particular formal language are sometimes called ''well-formed words''. A formal language is often defined by means of a formal grammar such as a regular grammar or context-free grammar. In computer science, formal languages are used, among others, as the basis for defining the grammar of programming languages and formalized versions of subsets of natural languages, in which the words of the language represent concepts that are associated with meanings or semantics. In computational complexity theory, decision problems are typically defined as formal languages, and complexity classes are defined as the sets of the formal languages that can be parsed by machines with limited computational power. In ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compiler Front-end
In computing, a compiler is a computer program that translates computer code written in one programming language (the ''source'' language) into another language (the ''target'' language). The name "compiler" is primarily used for programs that translate source code from a high-level programming language to a low-level programming language (e.g. assembly language, object code, or machine code) to create an executable program. Compilers: Principles, Techniques, and Tools by Alfred V. Aho, Ravi Sethi, Jeffrey D. Ullman - Second Edition, 2007 There are many different types of compilers which produce output in different useful forms. A ''cross-compiler'' produces code for a different CPU or operating system than the one on which the cross-compiler itself runs. A ''bootstrap compiler'' is often a temporary compiler, used for compiling a more permanent or better optimised compiler for a language. Related software include ''decompilers'', programs that translate from low-level la ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pumping Lemma For Context-free Languages
In computer science, in particular in formal language theory, the pumping lemma for context-free languages, also known as the Bar-Hillel lemma, is a lemma that gives a property shared by all context-free languages and generalizes the pumping lemma for regular languages. The pumping lemma can be used to construct a refutation by contradiction that a specific language is ''not'' context-free. Conversely, the pumping lemma does not suffice to guarantee that a language ''is'' context-free; there are other necessary conditions, such as Ogden's lemma, or the Interchange lemma. Formal statement If a language L is context-free, then there exists some integer p \geq 1 (called a "pumping length") (Also see s, \geq p) can be written as : s = uvwxy with substrings u, v, w, x and y, such that : 1. , vx, \geq 1, : 2. , vwx, \leq p, and : 3. uv^n wx^n y \in L for all n \geq 0. Below is a formal expression of the Pumping Lemma. \begin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kuroda Normal Form
In formal language theory, a noncontracting grammar is in Kuroda normal form if all production rules are of the form: :''AB'' → ''CD'' or :''A'' → ''BC'' or :''A'' → ''B'' or :''A'' → ''a'' where A, B, C and D are nonterminal symbols and ''a'' is a terminal symbol. Some sources omit the ''A'' → ''B'' pattern. It is named after Sige-Yuki Kuroda, who originally called it a linear bounded grammar, a terminology that was also used by a few other authors thereafter. Every grammar in Kuroda normal form is noncontracting, and therefore, generates a context-sensitive language. Conversely, every noncontracting grammar that does not generate the empty string can be converted to Kuroda normal form. A straightforward technique attributed to György Révész transforms a grammar in Kuroda normal form to a context-sensitive grammar: ''AB'' → ''CD'' is replaced by four context-sensitive rules ''AB'' → ''AZ'', ''AZ'' → ''WZ'', ''WZ'' → ''WD'' and ''WD'' → ''CD''. This pro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Greibach Normal Form
In formal language theory, a context-free grammar is in Greibach normal form (GNF) if the right-hand sides of all production rules start with a terminal symbol, optionally followed by some non-terminals. A non-strict form allows one exception to this format restriction for allowing the empty word (epsilon, ε) to be a member of the described language. The normal form was established by Sheila Greibach and it bears her name. More precisely, a context-free grammar is in Greibach normal form, if all production rules are of the form: :A \to a A_1 A_2 \cdots A_n where A is a nonterminal symbol, a is a terminal symbol, and A_1 A_2 \ldots A_n is a (possibly empty) sequence of nonterminal symbols. Observe that the grammar does not have left recursions. Every context-free grammar can be transformed into an equivalent grammar in Greibach normal form. Various constructions exist. Some do not permit the second form of rule and cannot transform context-free grammars that can generate the emp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bottom-up Parsing
In computer science, parsing reveals the grammatical structure of linear input text, as a first step in working out its meaning. Bottom-up parsing recognizes the text's lowest-level small details first, before its mid-level structures, and leaves the highest-level overall structure to last. Bottom-up versus top-down The bottom-up name comes from the concept of a parse tree, in which the most detailed parts are at the bottom of the upside-down tree, and larger structures composed from them are in successively higher layers, until at the top or "root" of the tree a single unit describes the entire input stream. A bottom-up parse discovers and processes that tree starting from the bottom left end, and incrementally works its way upwards and rightwards. Compilers: Principles, Techniques, and Tools (2nd Edition), by Alfred Aho Alfred Vaino Aho (born August 9, 1941) is a Canadian computer scientist best known for his work on programming languages, compilers, and related algorithms, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
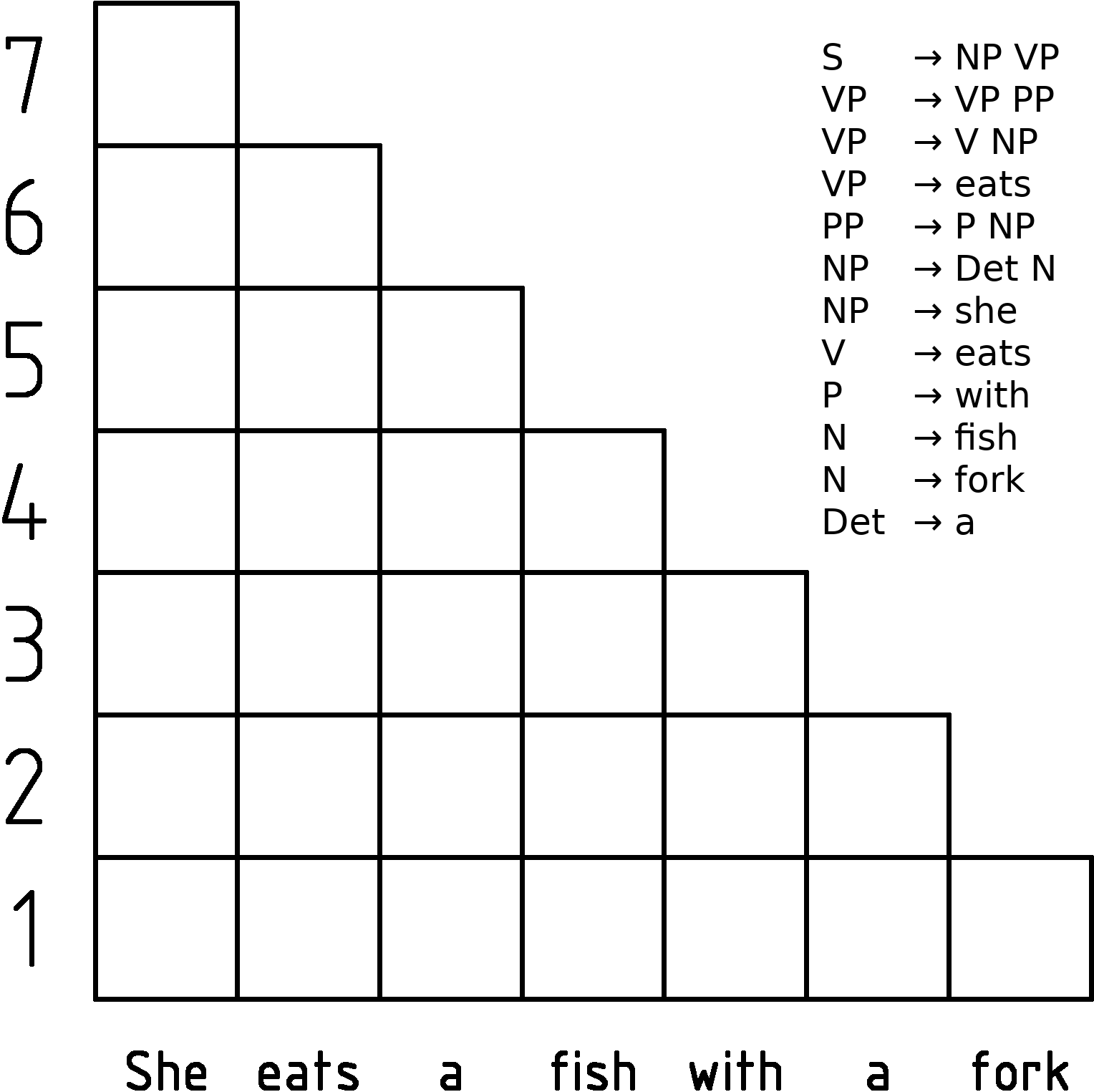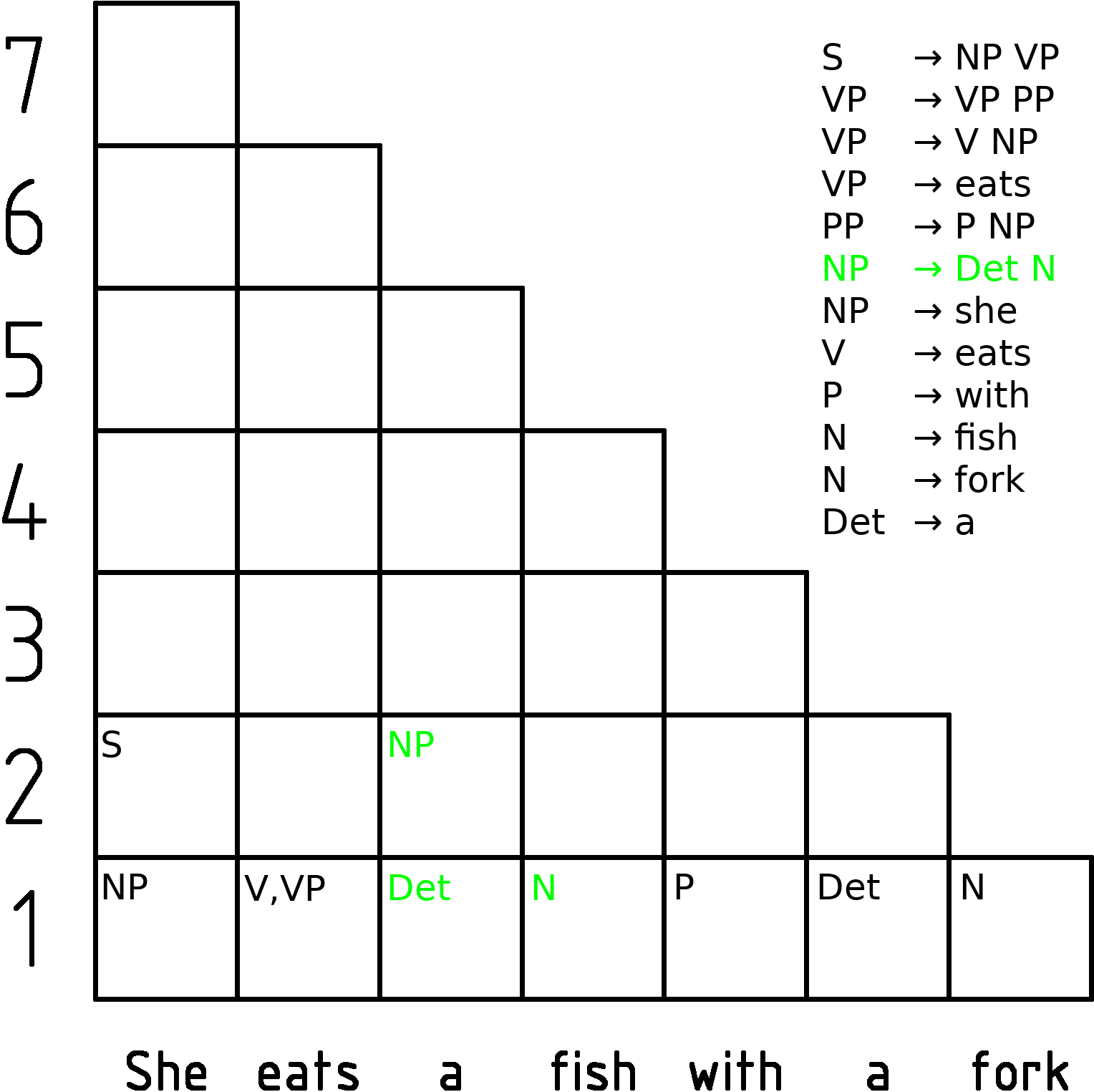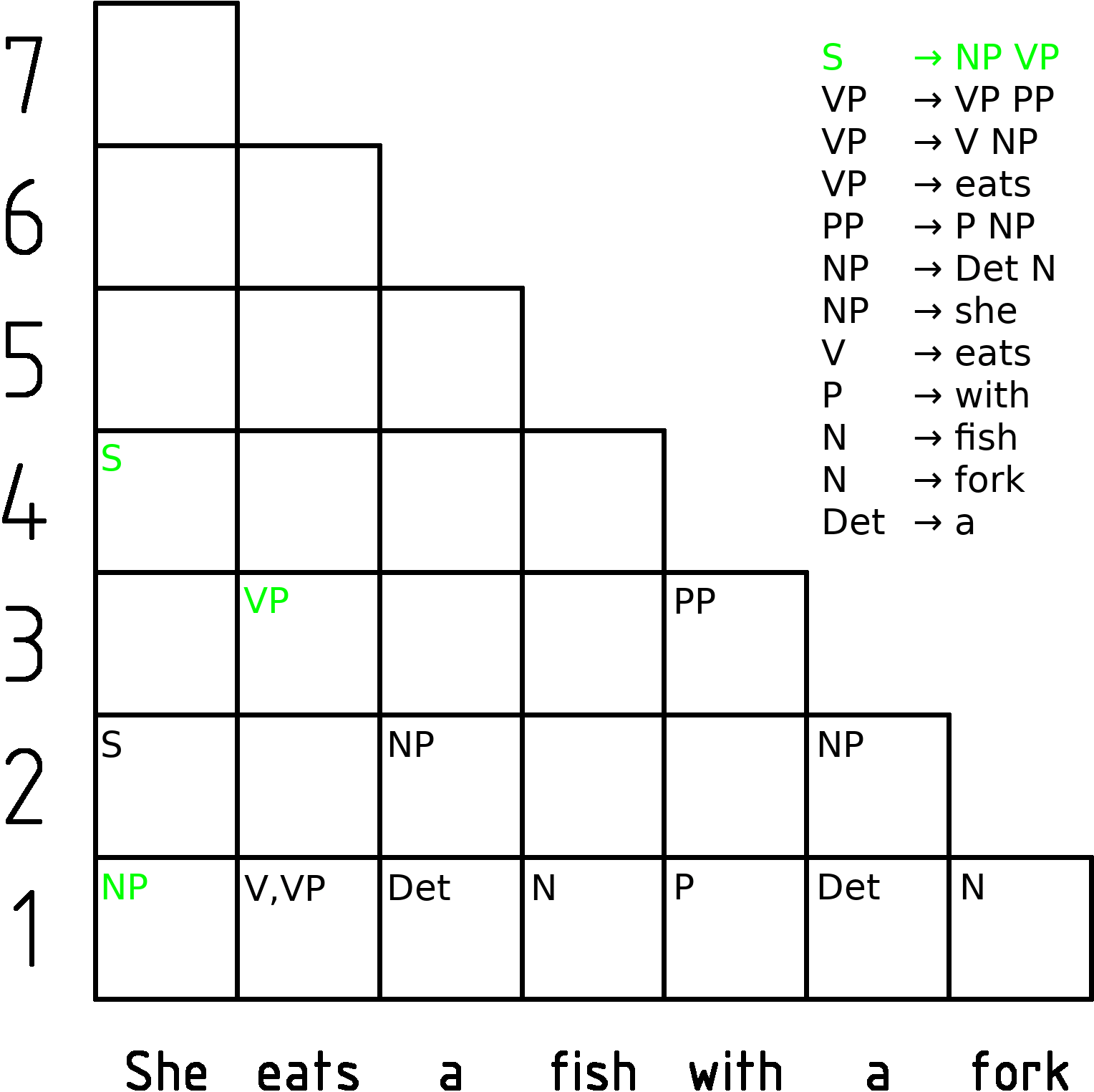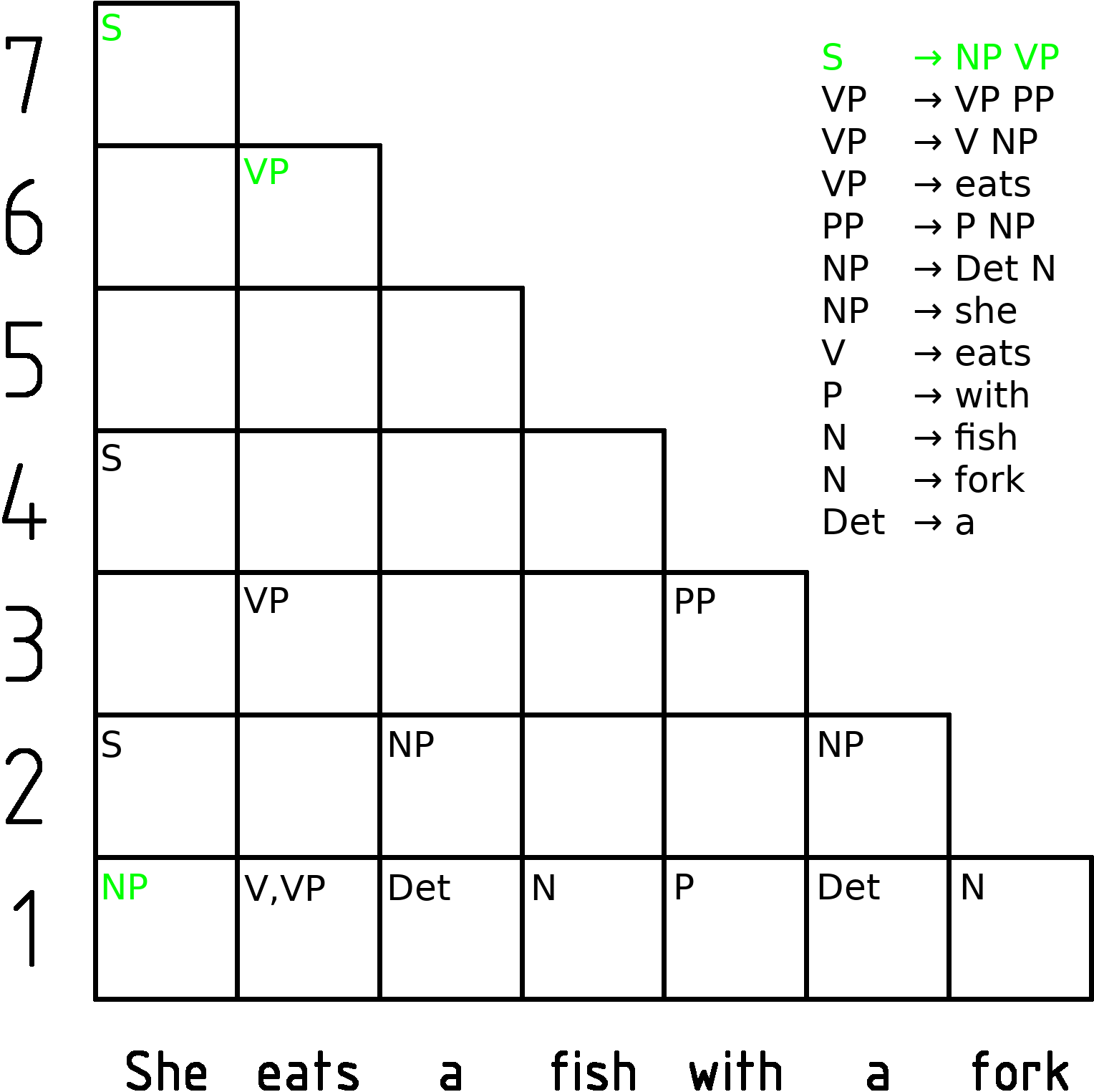
CYK Algorithm
In computer science, the Cocke–Younger–Kasami algorithm (alternatively called CYK, or CKY) is a parsing algorithm for context-free grammars published by Itiroo Sakai in 1961. The algorithm is named after some of its rediscoverers: John Cocke, Daniel Younger, Tadao Kasami, and Jacob T. Schwartz. It employs bottom-up parsing and dynamic programming. The standard version of CYK operates only on context-free grammars given in Chomsky normal form (CNF). However any context-free grammar may be algorithmically transformed into a CNF grammar expressing the same language . The importance of the CYK algorithm stems from its high efficiency in certain situations. Using big ''O'' notation, the worst case running time of CYK is \mathcal\left( n^3 \cdot \left, G \ \right), where n is the length of the parsed string and \left, G \ is the size of the CNF grammar G . This makes it one of the most efficient parsing algorithms in terms of worst-case asymptotic complexity, althoug ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Robert W
The name Robert is an ancient Germanic given name, from Proto-Germanic "fame" and "bright" (''Hrōþiberhtaz''). Compare Old Dutch ''Robrecht'' and Old High German ''Hrodebert'' (a compound of '' Hruod'' () "fame, glory, honour, praise, renown, godlike" and ''berht'' "bright, light, shining"). It is the second most frequently used given name of ancient Germanic origin.Reaney & Wilson, 1997. ''Dictionary of English Surnames''. Oxford University Press. It is also in use as a surname. Another commonly used form of the name is Rupert. After becoming widely used in Continental Europe, the name entered England in its Old French form ''Robert'', where an Old English cognate form (''Hrēodbēorht'', ''Hrodberht'', ''Hrēodbēorð'', ''Hrœdbœrð'', ''Hrœdberð'', ''Hrōðberχtŕ'') had existed before the Norman Conquest. The feminine version is Roberta. The Italian, Portuguese, and Spanish form is Roberto. Robert is also a common name in many Germanic languages, including En ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Donald E
Donald is a Scottish masculine given name. It is derived from the Goidelic languages, Gaelic name ''Dòmhnall''.. This comes from the Proto-Celtic language, Proto-Celtic *''Dumno-ualos'' ("world-ruler" or "world-wielder"). The final -''d'' in ''Donald'' is partly derived from a misinterpretation of the Gaelic pronunciation by English speakers. A short form of Donald is Don (given name), Don, and pet forms of Donald include Donnie and Donny. The feminine given name Donella (other) , Donella is derived from Donald. ''Donald'' has cognates in other Celtic languages: Irish language, Modern Irish ''Dónal'' (anglicised as ''Donal'' and ''Donall'');. Scottish Gaelic ''Dòmhnall'', ''Domhnull'' and ''Dòmhnull''; Welsh language, Welsh ''Dyfnwal (other), Dyfnwal'' and Cumbric ''Dumnagual''. Although the feminine given name ''Donna (given name), Donna'' is sometimes used as a feminine form of ''Donald'', the names are not etymologically related. Variations King ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Backus–Naur Form
In computer science, Backus–Naur form (BNF, pronounced ), also known as Backus normal form, is a notation system for defining the Syntax (programming languages), syntax of Programming language, programming languages and other Formal language, formal languages, developed by John Backus and Peter Naur. It is a metasyntax for Context-free grammar, context-free grammars, providing a precise way to outline the rules of a language's structure. It has been widely used in official specifications, manuals, and textbooks on programming language theory, as well as to describe Document format, document formats, Instruction set, instruction sets, and Communication protocol, communication protocols. Over time, variations such as extended Backus–Naur form (EBNF) and augmented Backus–Naur form (ABNF) have emerged, building on the original framework with added features. Structure BNF specifications outline how symbols are combined to form syntactically valid sequences. Each BNF consists of t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Formal Grammar
A formal grammar is a set of Terminal and nonterminal symbols, symbols and the Production (computer science), production rules for rewriting some of them into every possible string of a formal language over an Alphabet (formal languages), alphabet. A grammar does not describe the semantics, meaning of the strings — only their form. In applied mathematics, formal language theory is the discipline that studies formal grammars and languages. Its applications are found in theoretical computer science, theoretical linguistics, Formal semantics (logic), formal semantics, mathematical logic, and other areas. A formal grammar is a Set_(mathematics), set of rules for rewriting strings, along with a "start symbol" from which rewriting starts. Therefore, a grammar is usually thought of as a language generator. However, it can also sometimes be used as the basis for a "recognizer"—a function in computing that determines whether a given string belongs to the language or is grammatical ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Converting A Grammar To Chomsky Normal Form
Conversion or convert may refer to: Arts, entertainment, and media * ''The Convert'', a 2023 film produced by Jump Film & Television and Brouhaha Entertainment * "Conversion" (''Doctor Who'' audio), an episode of the audio drama ''Cyberman'' * "Conversion" (''Stargate Atlantis''), an episode of the television series ''Stargate Atlantis'' * "The Conversion" (''The Outer Limits''), a 1995 episode of the television series ''The Outer Limits'' * " Chapter 19: The Convert", an episode of the television series ''The Mandalorian'' Business and marketing * Conversion funnel, the path a consumer takes through the web toward or near a desired action or conversion * Conversion marketing, when a website's visitors take a desired action * Converting timber to commercial lumber Computing, science, and technology * Conversion of units, conversion between different units of measurement Computing and telecommunication * CHS conversion of data storage, mapping cylinder/head/sector tuples to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |