|
Charles Ehresmann
Charles Ehresmann (19 April 1905 – 22 September 1979) was a German-born French mathematician who worked in differential topology and category theory. He was an early member of the Bourbaki group, and is known for his work on the differential geometry of smooth fiber bundles, notably the introduction of the concepts of Ehresmann connection and of jet bundles, and for his seminar on category theory. Life Ehresmann was born in Strasbourg (at the time part of the German Empire) to an Alsatian-speaking family; his father was a gardener. After World War I, Alsace returned part of France and Ehresmann was taught in French at Lycée Kléber. Between 1924 and 1927 he studied at the École Normale Supérieure (ENS) in Paris and obtained agrégation in mathematics. After one year of military service, in 1928-29 he taught at a French school in Rabat, Morocco. He studied further at the University of Göttingen during the years 1930–31, and at Princeton University in 1932–34. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Research Institute Of Oberwolfach
The Oberwolfach Research Institute for Mathematics () is a center for mathematical research in Oberwolfach, Germany. It was founded by mathematician Wilhelm Süss in 1944. It organizes weekly workshops on diverse topics where mathematicians and scientists from all over the world come to do interdisciplinary, collaborative research. The Institute is a member of the Leibniz Association, funded mainly by the Federal Ministry of Education and Research (Germany), German Federal Ministry of Education and Research and by the state of Baden-Württemberg. It also receives substantial funding from the ''Friends of Oberwolfach'' foundation, from the ''Oberwolfach Foundation'' and from numerous donors. History The Oberwolfach Research Institute for Mathematics (MFO) was founded as the ''Reich Institute of Mathematics'' (German: ''Reichsinstitut für Mathematik'') on 1 September 1944. It was one of several research institutes founded by the Nazism, Nazis in order to further the German war ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
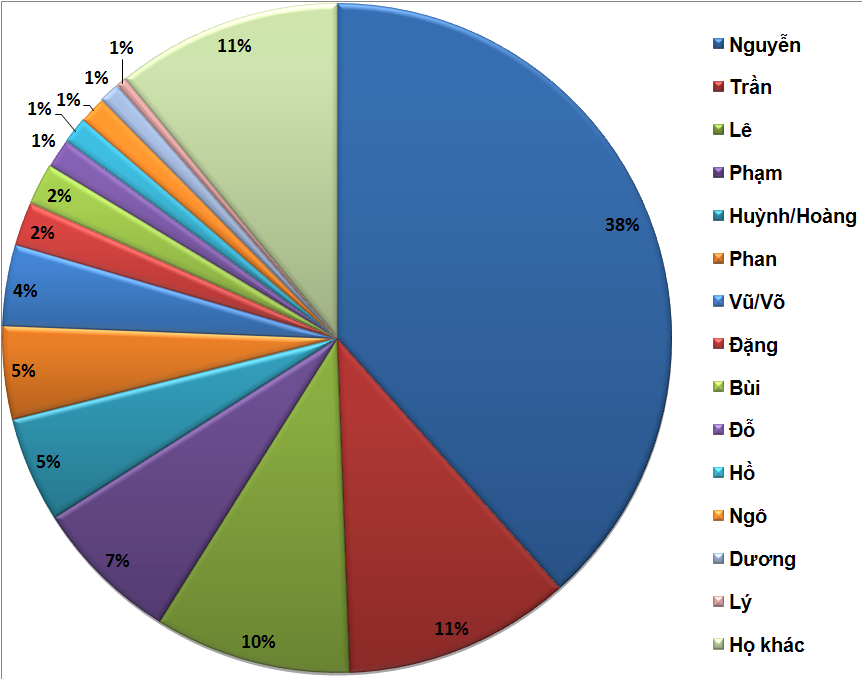
Nguyen Dinh Ngoc
Nguyễn (阮) (sometimes abbreviated as Ng̃) is the most common surname of the Vietnamese people. Outside of Vietnam, the surname is commonly rendered without diacritics as ''Nguyen''. By some estimates 30 to 39 percent of Vietnamese people bear this surname.Lê Trung Hoa, ''Họ và tên người Việt Nam'', NXB Khoa học - Xã hội, 2005 Origin and usage is the transcription of the Sino-Vietnamese pronunciation of the character 阮, which originally was used to write a name of a state in Gansu or ruan, an ancient Chinese instrument. The same Chinese character is often romanized as in Mandarin and as in Cantonese. The first recorded mention of a person surnamed Nguyễn is a description dating AD 317, of a journey to Giao Châu undertaken by Eastern Jin dynasty officer Nguyễn Phu and his family. Many events in Vietnamese history have contributed to the name's prominence. In 1232, after usurping the Lý dynasty, Trần Thủ Độ forced the descendants of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Differential Topology
In mathematics, differential topology is the field dealing with the topological properties and smooth properties of smooth manifolds. In this sense differential topology is distinct from the closely related field of differential geometry, which concerns the ''geometric'' properties of smooth manifolds, including notions of size, distance, and rigid shape. By comparison differential topology is concerned with coarser properties, such as the number of holes in a manifold, its homotopy type, or the structure of its diffeomorphism group. Because many of these coarser properties may be captured algebraically, differential topology has strong links to algebraic topology. The central goal of the field of differential topology is the classification of all smooth manifolds up to diffeomorphism. Since dimension is an invariant of smooth manifolds up to diffeomorphism type, this classification is often studied by classifying the ( connected) manifolds in each dimension separately: * In ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematician
A mathematician is someone who uses an extensive knowledge of mathematics in their work, typically to solve mathematical problems. Mathematicians are concerned with numbers, data, quantity, mathematical structure, structure, space, Mathematical model, models, and mathematics#Calculus and analysis, change. History One of the earliest known mathematicians was Thales of Miletus (); he has been hailed as the first true mathematician and the first known individual to whom a mathematical discovery has been attributed. He is credited with the first use of deductive reasoning applied to geometry, by deriving four corollaries to Thales's theorem. The number of known mathematicians grew when Pythagoras of Samos () established the Pythagorean school, whose doctrine it was that mathematics ruled the universe and whose motto was "All is number". It was the Pythagoreans who coined the term "mathematics", and with whom the study of mathematics for its own sake begins. The first woman math ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Andrée Ehresmann
Andrée Ehresmann (born Andrée Bastiani; 1935) is a French people, French mathematician specialising in category theory. Education and career Ehresmann was a researcher at Centre national de la recherche scientifique, CNRS from 1957 to 1963. She was awarded a Ph.D. in 1962 at University of Paris under the supervision of Gustave Choquet. Her thesis was entitled ''Différentiabilité dans les espaces localement convexes. Distructures'' [Differentiability in locally convex spaces. Distructures]. In 1967 she became a professor at IRCAM, at the University of Picardie Jules Verne, where she is currently emeritus professor. Research Ehresmann has published over a hundred works on Analysis (Differential Calculus and Infinite-dimensional Distributions, Guiding Systems and Optimization Problems), Category Theory (with her husband, Charles Ehresmann: sketches and internal categories, multiple categories, closed monoidal structures) and the modeling of complex autonomous systems (Memory ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prix Francoeur
The Prix Francoeur, or Francoeur Prize, was an award granted by the Institut de France, Academie des Sciences, Fondation Francoeur to authors of works useful to the progress of pure and applied mathematics. Preference was given to young scholars or to geometricians not yet established. It was established in 1882 and has been discontinued. Prize winners * 1882–1888 — Emile Barbier * 1889–1890 — Maximilien Marie * 1891–1892 — Augustin Mouchot * 1893 — Guy Robin * 1894 — J. Collet * 1895 — Jules Andrade * 1896 — Alphonse Valson * 1897 — Guy Robin * 1898 — Aimé Vaschy * 1899 — Le Cordier * 1900 — Edmond Maillet * 1901 — Léonce Laugel * 1902–1904 — Emile Lemoine * 1905 — Xavier Stouff * 1906–1912 — Emile Lemoine * 1913–1914 — A. Claude * 1915 — Joseph Marty * 1916 — René Gateaux * 1917 — Henri Villat * 1918 — Paul Montel * 1919 — Georges Giraud * 1920–1921 — René Baire * 1922 — Louis Antoine * 1923 — Gaston Bertran ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Strict 2-category
In category theory in mathematics, a 2-category is a category with "morphisms between morphisms", called 2-morphisms. A basic example is the category Cat of all (small) categories, where a 2-morphism is a natural transformation between functors. The concept of a strict 2-category was first introduced by Charles Ehresmann in his work on enriched categories in 1965. The more general concept of bicategory (or weak 2-category), where composition of morphisms is associative only up to a 2-isomorphism, was introduced in 1967 by Jean Bénabou. A (2, 1)-category is a 2-category where each 2-morphism is invertible. Definitions A strict 2-category By definition, a strict 2-category ''C'' consists of the data: * a class of 0-''cells'', * for each pairs of 0-cells a, b, a set \operatorname(a, b) called the set of 1-''cells'' from a to b, * for each pairs of 1-cells f, g in the same hom-set, a set \operatorname(f, g) called the set of 2-''cells'' from f to g, * ''ordinary composit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sketch (mathematics)
In the mathematical theory of categories, a sketch is a category ''D'', together with a set of cones intended to be limits and a set of cocones intended to be colimits. A model of the sketch in a category ''C'' is a functor :M:D\rightarrow C that takes each specified cone to a limit cone in ''C'' and each specified cocone to a colimit cocone in ''C''. Morphisms of models are natural transformations. Sketches are a general way of specifying structures on the objects of a category, forming a category-theoretic analog to the logical concept of a theory and its models A model is an informative representation of an object, person, or system. The term originally denoted the plans of a building in late 16th-century English, and derived via French and Italian ultimately from Latin , . Models can be divided int .... They allow multisorted models and models in any category. Sketches were invented in 1968 by Charles Ehresmann, using a different but equivalent definition. There a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lie Groupoid
In mathematics, a Lie groupoid is a groupoid where the set \operatorname of objects and the set \operatorname of morphisms are both manifolds, all the category operations (source and target, composition, identity-assigning map and inversion) are smooth, and the source and target operations :s,t : \operatorname \to \operatorname are submersions. A Lie groupoid can thus be thought of as a "many-object generalization" of a Lie group, just as a groupoid is a many-object generalization of a group. Accordingly, while Lie groups provide a natural model for (classical) continuous symmetries, Lie groupoids are often used as model for (and arise from) generalised, point-dependent symmetries. Extending the correspondence between Lie groups and Lie algebras, Lie groupoids are the global counterparts of Lie algebroids. Lie groupoids were introduced by Charles Ehresmann under the name ''differentiable groupoids''. Definition and basic concepts A Lie groupoid consists of * two smooth m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jet Bundle
In differential topology, the jet bundle is a certain construction that makes a new smooth fiber bundle out of a given smooth fiber bundle. It makes it possible to write differential equations on sections of a fiber bundle in an invariant form. Jets may also be seen as the coordinate free versions of Taylor expansions. Historically, jet bundles are attributed to Charles Ehresmann, and were an advance on the method ( prolongation) of Élie Cartan, of dealing ''geometrically'' with higher derivatives, by imposing differential form conditions on newly introduced formal variables. Jet bundles are sometimes called sprays, although sprays usually refer more specifically to the associated vector field induced on the corresponding bundle (e.g., the geodesic spray on Finsler manifolds.) Since the early 1980s, jet bundles have appeared as a concise way to describe phenomena associated with the derivatives of maps, particularly those associated with the calculus of variations. Conseq ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ehresmann Connection
In differential geometry, an Ehresmann connection (after the French mathematician Charles Ehresmann who first formalized this concept) is a version of the notion of a connection, which makes sense on any smooth fiber bundle. In particular, it does not rely on the possible vector bundle structure of the underlying fiber bundle, but nevertheless, linear connections may be viewed as a special case. Another important special case of Ehresmann connections are principal connections on principal bundles, which are required to be equivariant in the principal Lie group action. Introduction A covariant derivative in differential geometry is a linear differential operator which takes the directional derivative of a section of a vector bundle in a covariant manner. It also allows one to formulate a notion of a parallel section of a bundle in the direction of a vector: a section ''s'' is parallel along a vector X if \nabla_X s = 0. So a covariant derivative provides at least two things: ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ehresmann's Lemma
In mathematics, or specifically, in differential topology, Ehresmann's lemma or Ehresmann's fibration theorem states that if a smooth mapping f\colon M \rightarrow N, where M and N are smooth manifolds, is # a surjective submersion, and # a proper map (in particular, this condition is always satisfied if ''M'' is compact), then it is a locally trivial fibration. This is a foundational result in differential topology due to Charles Ehresmann, and has many variants. See also *Thom's first isotopy lemma References * * {{cite book, last1=Kolář, first1=Ivan, last2=Michor, first2=Peter W., last3=Slovák, first3=Jan, title=Natural operations in differential geometry, publisher=Springer-Verlag Springer Science+Business Media, commonly known as Springer, is a German multinational publishing company of books, e-books and peer-reviewed journals in science, humanities, technical and medical (STM) publishing. Originally founded in 1842 in ..., location=Berlin, year=1993, isbn=3-54 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |