|
Bicircular Curve
In geometry, a circular algebraic curve is a type of plane algebraic curve determined by an equation ''F''(''x'', ''y'') = 0, where ''F'' is a polynomial with real coefficients and the highest-order terms of ''F'' form a polynomial divisible by ''x''2 + ''y''2. More precisely, if ''F'' = ''F''''n'' + ''F''''n''−1 + ... + ''F''1 + ''F''0, where each ''F''''i'' is homogeneous of degree ''i'', then the curve ''F''(''x'', ''y'') = 0 is circular if and only if ''F''''n'' is divisible by ''x''2 + ''y''2. Equivalently, if the curve is determined in homogeneous coordinates by ''G''(''x'', ''y'', ''z'') = 0, where ''G'' is a homogeneous polynomial, then the curve is circular if and only if ''G''(1, ''i'', 0) = ''G''(1, −''i'', 0) = 0. In other words, the curve is circular if it contains the circular points at infinity, (1, ''i'', 0) and (1, −''i'',&nb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometry
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician who works in the field of geometry is called a ''List of geometers, geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point (geometry), point, line (geometry), line, plane (geometry), plane, distance, angle, surface (mathematics), surface, and curve, as fundamental concepts. Originally developed to model the physical world, geometry has applications in almost all sciences, and also in art, architecture, and other activities that are related to graphics. Geometry also has applications in areas of mathematics that are apparently unrelated. For example, methods of algebraic geometry are fundamental in Wiles's proof of Fermat's Last Theorem, Wiles's proof of Fermat's ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conchoid Of De Sluze
In algebraic geometry, the conchoids of de Sluze are a family of plane curves studied in 1662 by Walloon mathematician René François Walter, baron de Sluze. The curves are defined by the polar equation :r=\sec\theta+a\cos\theta \,. In cartesian coordinates, the curves satisfy the implicit equation :(x-1)(x^2+y^2)=ax^2 \, except that for the implicit form has an acnode not present in polar form. They are rational, circular, cubic plane curves. These expressions have an asymptote (for ). The point most distant from the asymptote is . is a crunode for . The area between the curve and the asymptote is, for , :, a, (1+a/4)\pi \, while for , the area is :\left(1-\frac a2\right)\sqrt-a\left(2+\frac a2\right)\arcsin\frac1. If , the curve will have a loop. The area of the loop is :\left(2+\frac a2\right)a\arccos\frac1 + \left(1-\frac a2\right)\sqrt. Four of the family have names of their own: *, line (asymptote to the rest of the family) *, cissoid of Diocles In geometr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
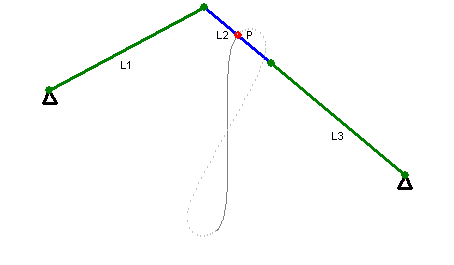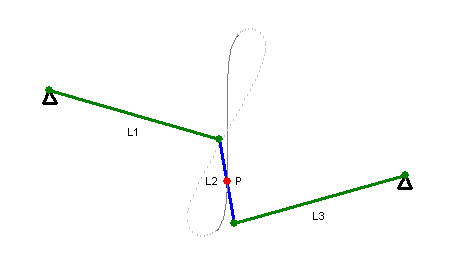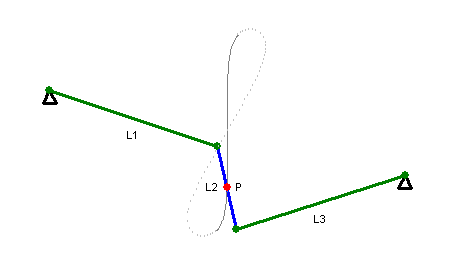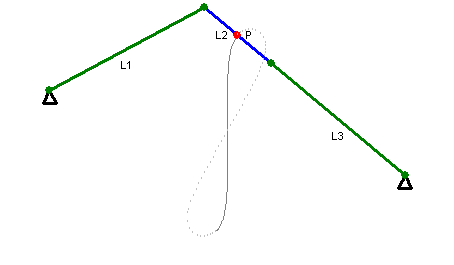
Watt's Curve
In mathematics, Watt's curve is a circular algebraic curve, tricircular algebraic curve, plane algebraic curve of sextic, degree six. It is generated by two circles of radius ''b'' with centers distance 2''a'' apart (taken to be at (±''a'', 0)). A line segment of length 2''c'' attaches to a point on each of the circles, and the midpoint of the line segment traces out the Watt curve as the circles rotate partially back and forth or completely around. It arose in connection with James Watt's pioneering work on the steam engine. The equation of the curve can be given in polar coordinates as :r^2=b^2-\left[a\sin\theta\pm\sqrt\right]^2. Derivation Polar coordinates The polar equation for the curve can be derived as follows: Working in the complex plane, let the centers of the circles be at ''a'' and ''−a'', and the connecting segment have endpoints at ''−a''+''be''''i'' λ and ''a''+''be''''i'' ρ. Let the angle of inclination of the segment be ψ with its midpoint at ''re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cardioid
In geometry, a cardioid () is a plane curve traced by a point on the perimeter of a circle that is rolling around a fixed circle of the same radius. It can also be defined as an epicycloid having a single cusp. It is also a type of sinusoidal spiral, and an inverse curve of the parabola with the focus as the center of inversion. A cardioid can also be defined as the set of points of reflections of a fixed point on a circle through all tangents to the circle. The name was coined by Giovanni Salvemini in 1741 but the cardioid had been the subject of study decades beforehand.Yates Although named for its heart-like form, it is shaped more like the outline of the cross-section of a round apple without the stalk. A cardioid microphone exhibits an acoustic pickup pattern that, when graphed in two dimensions, resembles a cardioid (any 2d plane containing the 3d straight line of the microphone body). In three dimensions, the cardioid is shaped like an apple centred around the mic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Limaçon
In geometry, a limaçon or limacon , also known as a limaçon of Pascal or Pascal's Snail, is defined as a roulette curve formed by the path of a point fixed to a circle when that circle rolls around the outside of a circle of equal radius. It can also be defined as the roulette formed when a circle rolls around a circle with half its radius so that the smaller circle is inside the larger circle. Thus, they belong to the family of curves called centered trochoids; more specifically, they are epitrochoids. The cardioid is the special case in which the point generating the roulette lies on the rolling circle; the resulting curve has a cusp. Depending on the position of the point generating the curve, it may have inner and outer loops (giving the family its name), it may be heart-shaped, or it may be oval. A limaçon is a bicircular rational plane algebraic curve of degree 4. History The earliest formal research on limaçons is generally attributed to Étienne Pascal, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Toric Section
A toric section is an intersection of a plane with a torus, just as a conic section is the intersection of a plane with a cone. Special cases have been known since antiquity, and the general case was studied by Jean Gaston Darboux.. Mathematical formulae In general, toric sections are fourth-order ( quartic) plane curves of the form : \left( x^2 + y^2 \right)^2 + a x^2 + b y^2 + cx + dy + e = 0. Spiric sections A special case of a toric section is the spiric section, in which the intersecting plane is parallel to the rotational symmetry axis of the torus. They were discovered by the ancient Greek geometer Perseus in roughly 150 BC. Well-known examples include the hippopede and the Cassini oval and their relatives, such as the lemniscate of Bernoulli. Villarceau circles Another special case is the Villarceau circles, in which the intersection is a circle despite the lack of any of the obvious sorts of symmetry that would entail a circular cross-section.. General toric ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lemniscate Of Bernoulli
In geometry, the lemniscate of Bernoulli is a plane curve defined from two given points and , known as foci, at distance from each other as the locus of points so that . The curve has a shape similar to the numeral 8 and to the ∞ symbol. Its name is from , which is Latin for "decorated with hanging ribbons". It is a special case of the Cassini oval and is a rational algebraic curve of degree 4. This lemniscate was first described in 1694 by Jakob Bernoulli as a modification of an ellipse, which is the locus of points for which the sum of the distances to each of two fixed ''focal points'' is a constant. A Cassini oval, by contrast, is the locus of points for which the ''product'' of these distances is constant. In the case where the curve passes through the point midway between the foci, the oval is a lemniscate of Bernoulli. This curve can be obtained as the inverse transform of a hyperbola, with the inversion circle centered at the center of the hyperbola (bisect ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cassini Oval
In geometry, a Cassini oval is a quartic plane curve defined as the locus of points in the plane such that the product of the distances to two fixed points (foci) is constant. This may be contrasted with an ellipse, for which the ''sum'' of the distances is constant, rather than the product. Cassini ovals are the special case of polynomial lemniscates when the polynomial used has degree 2. Cassini ovals are named after the astronomer Giovanni Domenico Cassini who studied them in the late 17th century. Cassini believed that a planet orbiting around another body traveled on one of these ovals, with the body it orbited around at one focus of the oval. Other names include Cassinian ovals, Cassinian curves and ovals of Cassini. Formal definition A Cassini oval is a set of points, such that for any point P of the set, the ''product'' of the distances , PP_1, ,\, , PP_2, to two fixed points P_1, P_2 is a constant, usually written as b^2 where b > 0: :\\ . As with an ellipse, th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circle
A circle is a shape consisting of all point (geometry), points in a plane (mathematics), plane that are at a given distance from a given point, the Centre (geometry), centre. The distance between any point of the circle and the centre is called the radius. The length of a line segment connecting two points on the circle and passing through the centre is called the diameter. A circle bounds a region of the plane called a Disk (mathematics), disc. The circle has been known since before the beginning of recorded history. Natural circles are common, such as the full moon or a slice of round fruit. The circle is the basis for the wheel, which, with related inventions such as gears, makes much of modern machinery possible. In mathematics, the study of the circle has helped inspire the development of geometry, astronomy and calculus. Terminology * Annulus (mathematics), Annulus: a ring-shaped object, the region bounded by two concentric circles. * Circular arc, Arc: any Connected ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Plane Algebraic Curve
In mathematics, an affine algebraic plane curve is the zero set of a polynomial in two variables. A projective algebraic plane curve is the zero set in a projective plane of a homogeneous polynomial in three variables. An affine algebraic plane curve can be completed in a projective algebraic plane curve by homogenizing its defining polynomial. Conversely, a projective algebraic plane curve of homogeneous equation can be restricted to the affine algebraic plane curve of equation . These two operations are each inverse to the other; therefore, the phrase algebraic plane curve is often used without specifying explicitly whether it is the affine or the projective case that is considered. If the defining polynomial of a plane algebraic curve is irreducible, then one has an ''irreducible plane algebraic curve''. Otherwise, the algebraic curve is the union of one or several irreducible curves, called its ''components'', that are defined by the irreducible factors. More generally, an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inversive Geometry
In geometry, inversive geometry is the study of ''inversion'', a transformation of the Euclidean plane that maps circles or lines to other circles or lines and that preserves the angles between crossing curves. Many difficult problems in geometry become much more tractable when an inversion is applied. Inversion seems to have been discovered by a number of people contemporaneously, including Steiner (1824), Quetelet (1825), Bellavitis (1836), Stubbs and Ingram (1842–3) and Kelvin (1845). The concept of inversion can be generalized to higher-dimensional spaces. Inversion in a circle Inverse of a point To invert a number in arithmetic usually means to take its reciprocal. A closely related idea in geometry is that of "inverting" a point. In the plane, the inverse of a point ''P'' with respect to a ''reference circle (Ø)'' with center ''O'' and radius ''r'' is a point ''P'', lying on the ray from ''O'' through ''P'' such that :OP \cdot OP^ = r^2. This is calle ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclidean Group
In mathematics, a Euclidean group is the group of (Euclidean) isometries of a Euclidean space \mathbb^n; that is, the transformations of that space that preserve the Euclidean distance between any two points (also called Euclidean transformations). The group depends only on the dimension ''n'' of the space, and is commonly denoted E(''n'') or ISO(''n''), for ''inhomogeneous special orthogonal'' group. The Euclidean group E(''n'') comprises all translations, rotations, and reflections of \mathbb^n; and arbitrary finite combinations of them. The Euclidean group can be seen as the symmetry group of the space itself, and contains the group of symmetries of any figure (subset) of that space. A Euclidean isometry can be ''direct'' or ''indirect'', depending on whether it preserves the handedness of figures. The direct Euclidean isometries form a subgroup, the special Euclidean group, often denoted SE(''n'') and E+(''n''), whose elements are called rigid motions or Euclidean ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |