|
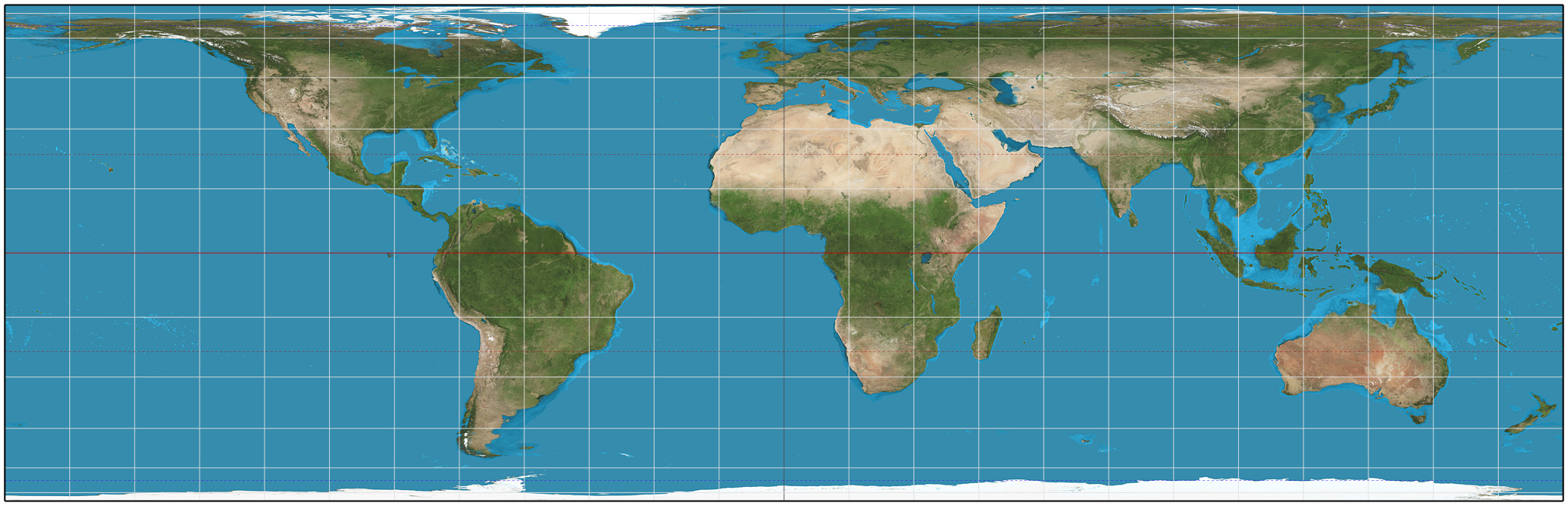
Behrmann Projection
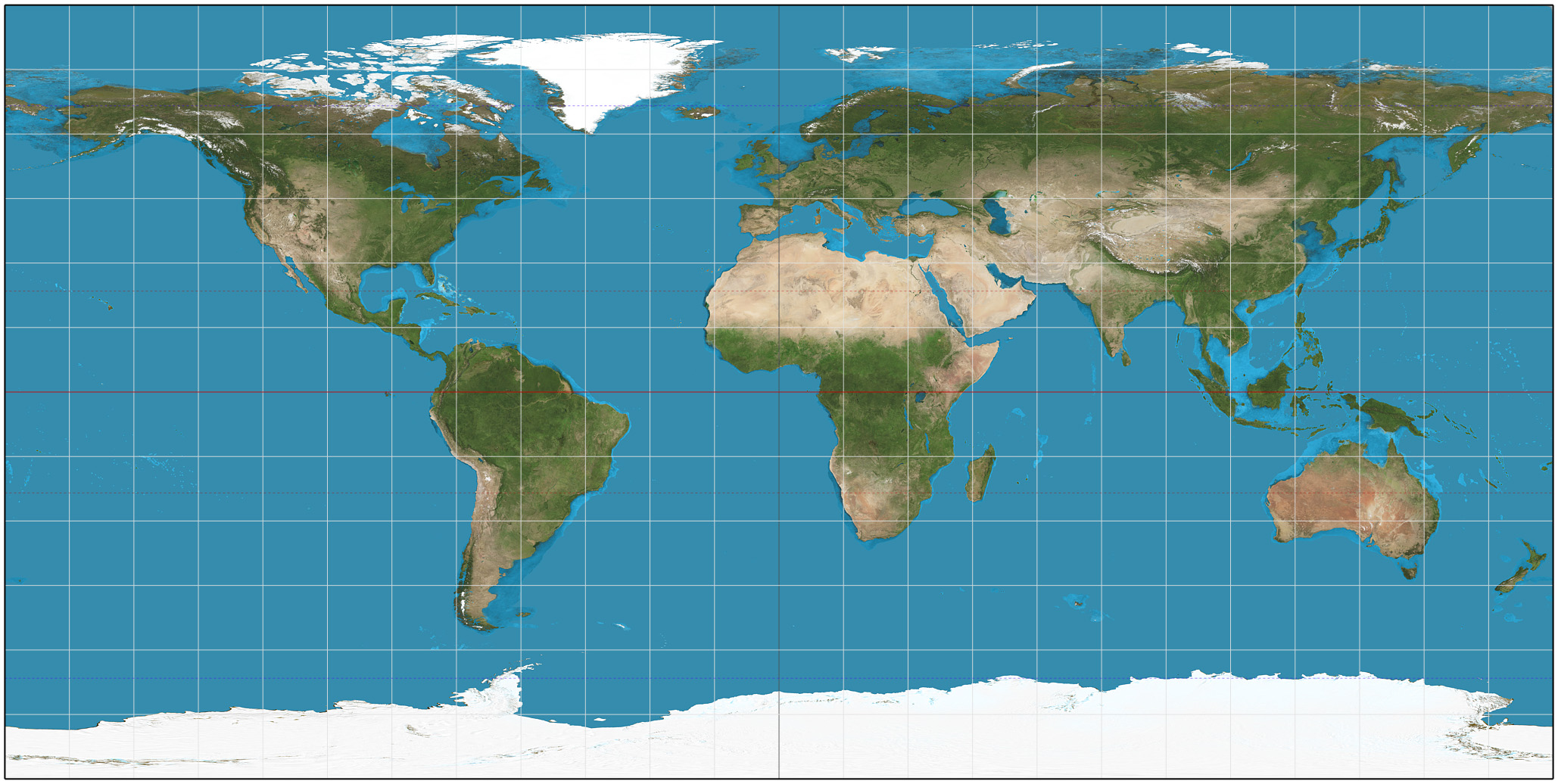
The Behrmann projection is a cylindrical equal-area projection, cylindrical equal-area map projection described by Walter Behrmann in 1910. Cylindrical equal-area projections differ by their standard parallels, which are Parallels of latitude, parallels along which the projection has no distortion. In the case of the Behrmann projection, the standard parallels are 30°N and 30°S. While equal-area, distortion of shape increases in the Behrmann projection according to distance from the standard parallels. The Behrmann projection has the property that half of the Earth's surface is stretched horizontally and the other half is stretched vertically. This projection is not Map projection#Equidistant, equidistant. See also *List of map projections References External links *Table of examples and properties of all common projections from radicalcartography.net Cylindrical equal-area projections {{cartography-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cylindrical Equal-area Projection
In cartography, the normal cylindrical equal-area projection is a family of Map projection#Normal cylindrical, normal cylindrical, equal-area projection, equal-area map projections. History The invention of the Lambert cylindrical equal-area projection is attributed to the Switzerland, Swiss mathematician Johann Heinrich Lambert in 1772. Variations of it appeared over the years by inventors who stretched the height of the Lambert and compressed the width commensurately in various ratios. Description The projection: * is Map_projection#Cylindrical, cylindrical, that means it has a cylindrical projection surface * is normal, that means it has a normal Map projection#Aspect, aspect * is an equal-area projection, that means any two areas in the map have the same relative size compared to their size on the sphere. The term "normal cylindrical projection" is used to refer to any projection in which Meridian (geography), meridians are mapped to equally spaced vertical lines and cir ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Behrmann Projection SW
Behrmann is a German surname. Notable people with the surname include: * Lazar Behrmann (1830–1893), Russian educator and editor *Marlene Behrmann (born 1959), American psychologist * Michael Behrmann (born 1966), German field hockey coach *Walter Behrmann (1882–1955), German geographer See also *Behrmann projection The Behrmann projection is a cylindrical equal-area projection, cylindrical equal-area map projection described by Walter Behrmann in 1910. Cylindrical equal-area projections differ by their standard parallels, which are Parallels of latitude, p ... * Behrman {{surname, Behrmann German-language surnames ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tissot Indicatrix World Map Behrmann Equal-area Proj
Tissot SA () is a Swiss luxury watch brand owned by the Swatch Group. The company was founded in Le Locle, Switzerland by Charles-Félicien Tissot and his son, Charles-Émile Tissot, in 1853. Tissot is not associated with Mathey-Tissot, another Swiss watchmaking firm. History Independent company Tissot was founded in 1853 by Charles-Félicien Tissot and his son Charles-Émile Tissot in the Swiss city of Le Locle, in the Neuchâtel canton of the Jura Mountains area. The father and son team worked as a casemaker (Charles-Félicien Tissot) and watchmaker (Charles-Emile). His son having expressed an interest in watchmaking from a young age. The two turned their house at the time into a small 'factory'. Charles-Emile Tissot left for Russia in 1858 and succeeded in selling their savonnette pocket watches across the Russian Empire. Russia became Tissot's greatest market, with the brand gaining popularity even in the Tsar's court; so Charles Tissot, Charles-Émile's son, moved to Mo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Map Projection
In cartography, a map projection is any of a broad set of Transformation (function) , transformations employed to represent the curved two-dimensional Surface (mathematics), surface of a globe on a Plane (mathematics), plane. In a map projection, coordinates, often expressed as latitude and longitude, of locations from the surface of the globe are transformed to coordinates on a plane. Projection is a necessary step in creating a two-dimensional map and is one of the essential elements of cartography. All projections of a sphere on a plane necessarily distort the surface in some way. Depending on the purpose of the map, some distortions are acceptable and others are not; therefore, different map projections exist in order to preserve some properties of the sphere-like body at the expense of other properties. The study of map projections is primarily about the characterization of their distortions. There is no limit to the number of possible map projections. More generally, proje ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Walter Behrmann
Walter Emmerich Behrmann (May 22, 1882, Oldenburg – May 3, 1955, Berlin) was a German geographer. He is remembered for introducing a cylindrical map projection known as the "Behrmann projection". Biography From 1901 to 1905, he studied geography, mathematics and physics at the University of Göttingen, where he was a student of Hermann Wagner. Later on, he worked as an assistant to geographer Joseph Partsch at the University of Leipzig (1908/09).Leibniz Institut für Länderkunde biographical sketch In 1912/13 he participated as a geographer in the ''Kaiserin-Augusta-Fluss Expedition'' to along with [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parallels Of Latitude
A circle of latitude or line of latitude on Earth is an abstract east–west small circle connecting all locations around Earth (ignoring elevation) at a given latitude coordinate line. Circles of latitude are often called parallels because they are parallel to each other; that is, planes that contain any of these circles never intersect each other. A location's position along a circle of latitude is given by its longitude. Circles of latitude are unlike circles of longitude, which are all great circles with the centre of Earth in the middle, as the circles of latitude get smaller as the distance from the Equator increases. Their length can be calculated by a common sine or cosine function. For example, the 60th parallel north or south is half as long as the Equator (disregarding Earth's minor flattening by 0.335%), stemming from \cos(60^) = 0.5. On the Mercator projection or on the Gall-Peters projection, a circle of latitude is perpendicular to all meridians. On the ell ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Map Projection
In cartography, a map projection is any of a broad set of Transformation (function) , transformations employed to represent the curved two-dimensional Surface (mathematics), surface of a globe on a Plane (mathematics), plane. In a map projection, coordinates, often expressed as latitude and longitude, of locations from the surface of the globe are transformed to coordinates on a plane. Projection is a necessary step in creating a two-dimensional map and is one of the essential elements of cartography. All projections of a sphere on a plane necessarily distort the surface in some way. Depending on the purpose of the map, some distortions are acceptable and others are not; therefore, different map projections exist in order to preserve some properties of the sphere-like body at the expense of other properties. The study of map projections is primarily about the characterization of their distortions. There is no limit to the number of possible map projections. More generally, proje ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
List Of Map Projections
This is a summary of map projections that have articles of their own on Wikipedia or that are otherwise WP:NOTABLE, notable. Because there is no limit to the number of possible map projections, there can be no comprehensive list. Table of projections *The first known popularizer/user and not necessarily the creator. Key Type of projection surface ; Cylindrical: In normal aspect, these map regularly-spaced meridians to equally spaced vertical lines, and parallels to horizontal lines. ; Pseudocylindrical: In normal aspect, these map the central meridian and parallels as straight lines. Other meridians are curves (or possibly straight from pole to equator), regularly spaced along parallels. ; Conic: In normal aspect, conic (or conical) projections map meridians as straight lines, and parallels as arcs of circles. ; Pseudoconical: In normal aspect, pseudoconical projections represent the central meridian as a straight line, other meridians as complex curves, and parallels as ci ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |