|
Bandwidth-limited Pulse
A bandwidth-limited pulse (also known as Fourier-transform-limited pulse, or more commonly, transform-limited pulse) is a pulse of a wave that has the minimum possible duration for a given spectral bandwidth. Bandwidth-limited pulses have a constant phase across all frequencies making up the pulse. Optical pulses of this type can be generated by mode-locked lasers. Any waveform can be disassembled into its spectral components by Fourier analysis or Fourier transformation. The length of a pulse thereby is determined by its spectral components, which include not just their relative intensities, but also the relative positions ( spectral phase) of these spectral components. For different pulse shapes, the minimum duration-bandwidth product is different. The duration-bandwidth product is minimal for zero phase-modulation. For example, \mathrm pulses have a minimum duration-bandwidth product of 0.315 while gaussian pulses have a minimum value of 0.441. A bandwidth-limited pulse ca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fourier Transform
In mathematics, the Fourier transform (FT) is an integral transform that takes a function as input then outputs another function that describes the extent to which various frequencies are present in the original function. The output of the transform is a complex-valued function of frequency. The term ''Fourier transform'' refers to both this complex-valued function and the mathematical operation. When a distinction needs to be made, the output of the operation is sometimes called the frequency domain representation of the original function. The Fourier transform is analogous to decomposing the sound of a musical chord into the intensities of its constituent pitches. Functions that are localized in the time domain have Fourier transforms that are spread out across the frequency domain and vice versa, a phenomenon known as the uncertainty principle. The critical case for this principle is the Gaussian function, of substantial importance in probability theory and statist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kerr-lens Modelocking
Kerr-lens mode-locking (KLM) is a method of mode-locking lasers via the nonlinear optical Kerr effect. This method allows the generation of pulses of light with a duration as short as a few femtoseconds. The optical Kerr effect is a process which results from the nonlinear response of an optical medium to the electric field of an electromagnetic wave. The refractive index of the medium is dependent on the field strength. Because of the non-uniform power density distribution in a Gaussian beam (as found in laser resonators) the refractive index changes across the beam profile; the refractive index experienced by the beam is greater in the center of the beam than at the edge. Thus a rod of an active Kerr medium functions as a lens for high intensity light. This is called self-focusing and in extreme cases leads to material destruction. In the laser cavity short bursts of light will then be focused differently from continuous waves. To favor the pulsed mode over continuous-wave, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Group Velocity Dispersion
In optics, group-velocity dispersion (GVD) is a characteristic of a dispersive medium, used most often to determine how the medium affects the duration of an optical pulse traveling through it. Formally, GVD is defined as the derivative of the inverse of group velocity of light in a material with respect to angular frequency, : \text(\omega_0) \equiv \frac \left( \frac \right)_, where \omega and \omega_0 are angular frequencies, and the group velocity v_g(\omega) is defined as v_g(\omega) \equiv \partial \omega / \partial k. The units of group-velocity dispersion are imesup>2/ istance often expressed in fs2/ mm. Equivalently, group-velocity dispersion can be defined in terms of the medium-dependent wave vector k(\omega) according to : \text(\omega_0) \equiv \left( \frac\right)_, or in terms of the refractive index n(\omega) according to : \text(\omega_0) \equiv \frac \left(\frac\right)_ + \frac\left( \frac\right)_. Applications Group-velocity dispersion is most commo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ultrashort Pulse
In optics, an ultrashort pulse, also known as an ultrafast event, is an electromagnetic pulse whose time duration is of the order of a picosecond (10−12 second) or less. Such pulses have a broadband optical spectrum, and can be created by mode-locked oscillators. Amplification of ultrashort pulses almost always requires the technique of chirped pulse amplification, in order to avoid damage to the gain medium of the amplifier. They are characterized by a high peak intensity (or more correctly, irradiance) that usually leads to nonlinear interactions in various materials, including air. These processes are studied in the field of nonlinear optics. In the specialized literature, "ultrashort" refers to the femtosecond (fs) and picosecond (ps) range, although such pulses no longer hold the record for the shortest pulses artificially generated. Indeed, x-ray pulses with durations on the attosecond time scale have been reported. The 1999 Nobel Prize in Chemistry was awar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dispersion Management
Dispersion may refer to: Economics and finance *Dispersion (finance), a measure for the statistical distribution of portfolio returns *Price dispersion, a variation in prices across sellers of the same item *Wage dispersion, the amount of variation in wages encountered in an economy *Dispersed knowledge, notion that any one person is unable to perceive all economic forces Science and mathematics Mathematics *Statistical dispersion, a quantifiable variation of measurements of differing members of a population **Index of dispersion, a normalized measure of the dispersion of a probability distribution * Dispersion point, a point in a topological space the removal of which leaves the space highly disconnected Physics *The dependence of wave velocity on frequency or wavelength: **Dispersion (optics), for light waves **Dispersion (water waves), for water waves **Acoustic dispersion, for sound waves **Dispersion relation, the mathematical description of dispersion in a system **Modal di ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
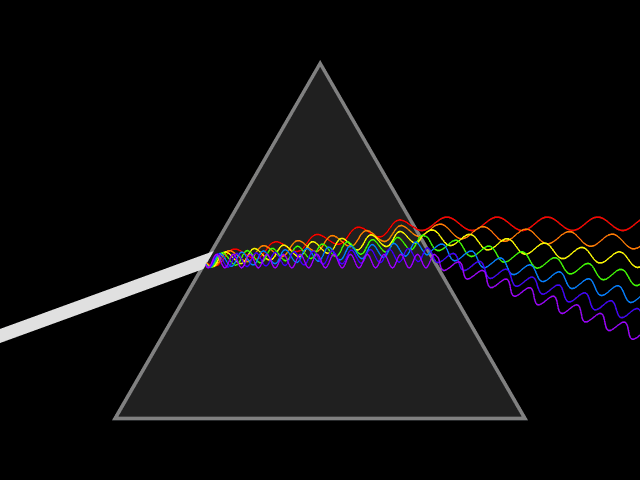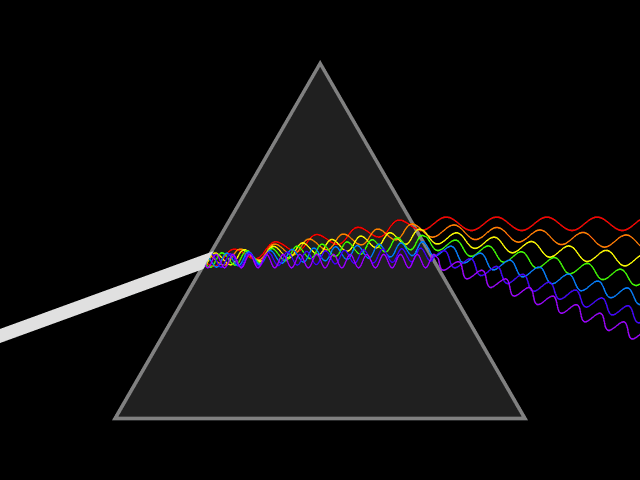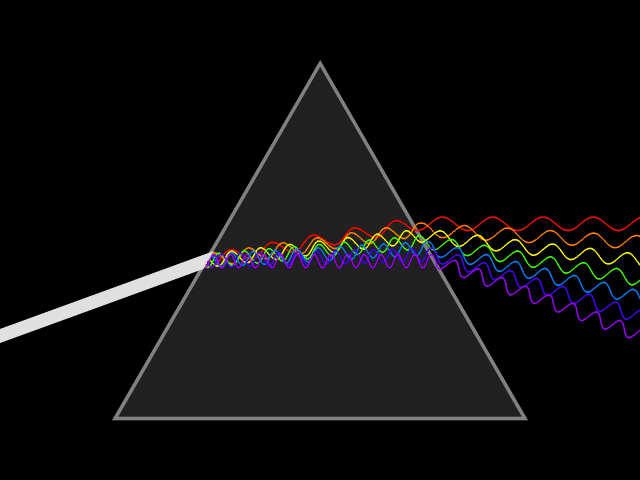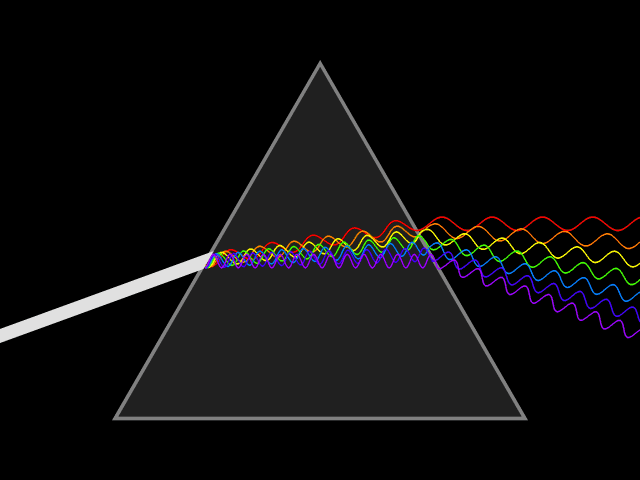
Dispersion (optics)
Dispersion is the phenomenon in which the phase velocity of a wave depends on its frequency. Sometimes the term chromatic dispersion is used to refer to optics specifically, as opposed to wave propagation in general. A medium having this common property may be termed a dispersive medium. Although the term is used in the field of optics to describe light and other electromagnetic waves, dispersion in the same sense can apply to any sort of wave motion such as acoustic dispersion in the case of sound and seismic waves, and in gravity waves (ocean waves). Within optics, dispersion is a property of telecommunication signals along transmission lines (such as microwaves in coaxial cable) or the Pulse (signal processing), pulses of light in optical fiber. In optics, one important and familiar consequence of dispersion is the change in the angle of refraction of different colors of light, as seen in the spectrum produced by a dispersive Prism (optics), prism and in chromatic aberration ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spectral Phase
In signal processing, the power spectrum S_(f) of a continuous time signal x(t) describes the distribution of power into frequency components f composing that signal. According to Fourier analysis, any physical signal can be decomposed into a number of discrete frequencies, or a spectrum of frequencies over a continuous range. The statistical average of any sort of signal (including noise) as analyzed in terms of its frequency content, is called its spectrum. When the energy of the signal is concentrated around a finite time interval, especially if its total energy is finite, one may compute the energy spectral density. More commonly used is the power spectral density (PSD, or simply power spectrum), which applies to signals existing over ''all'' time, or over a time period large enough (especially in relation to the duration of a measurement) that it could as well have been over an infinite time interval. The PSD then refers to the spectral energy distribution that would be f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Value
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the form a + bi, where and are real numbers. Because no real number satisfies the above equation, was called an imaginary number by René Descartes. For the complex number is called the , and is called the . The set of complex numbers is denoted by either of the symbols \mathbb C or . Despite the historical nomenclature, "imaginary" complex numbers have a mathematical existence as firm as that of the real numbers, and they are fundamental tools in the scientific description of the natural world. Complex numbers allow solutions to all polynomial equations, even those that have no solutions in real numbers. More precisely, the fundamental theorem of algebra asserts that every non-constant polynomial equation with real or complex coefficients h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fourier Analysis
In mathematics, Fourier analysis () is the study of the way general functions may be represented or approximated by sums of simpler trigonometric functions. Fourier analysis grew from the study of Fourier series, and is named after Joseph Fourier, who showed that representing a function as a sum of trigonometric functions greatly simplifies the study of heat transfer. The subject of Fourier analysis encompasses a vast spectrum of mathematics. In the sciences and engineering, the process of decomposing a function into oscillatory components is often called Fourier analysis, while the operation of rebuilding the function from these pieces is known as Fourier synthesis. For example, determining what component frequencies are present in a musical note would involve computing the Fourier transform of a sampled musical note. One could then re-synthesize the same sound by including the frequency components as revealed in the Fourier analysis. In mathematics, the term ''Fourier an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pulse (physics)
In physics, a pulse is a generic term describing a single disturbance that moves through a transmission medium. This medium may be vacuum (in the case of electromagnetic radiation) or matter, and may be indefinitely large or finite. Pulse reflection Consider a pulse moving through a medium - perhaps through a rope or a slinky. When the pulse reaches the end of that medium, what happens to it depends on whether the medium is fixed in space or free to move at its end. For example, if the pulse is moving through a rope and the end of the rope is held firmly by a person, then it is said that the pulse is approaching a fixed end. On the other hand, if the end of the rope is fixed to a stick such that it is free to move up or down along the stick when the pulse reaches its end, then it is said that the pulse is approaching a free end. Free end A pulse will reflect off a free end and return with the same direction of displacement that it had before reflection. That is, a pulse with a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spectral Component
In psychoacoustics, a pure tone is a sound with a sinusoidal waveform; that is, a sine wave of constant frequency, phase-shift, and amplitude. By extension, in signal processing a single-frequency tone or pure tone is a purely sinusoidal signal (e.g., a voltage). A pure tone has the property – unique among real-valued wave shapes – that its wave shape is unchanged by linear time-invariant systems; that is, only the phase and amplitude change between such a system's pure-tone input and its output. Sine and cosine waves can be used as basic building blocks of more complex waves. As additional sine waves having different frequencies are combined, the waveform transforms from a sinusoidal shape into a more complex shape. When considered as part of a whole spectrum, a pure tone may also be called a ''spectral component''. In clinical audiology, pure tones are used for pure-tone audiometry to characterize hearing thresholds at different frequencies. Sound localization is often ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |