|
Axial Multipole Moments
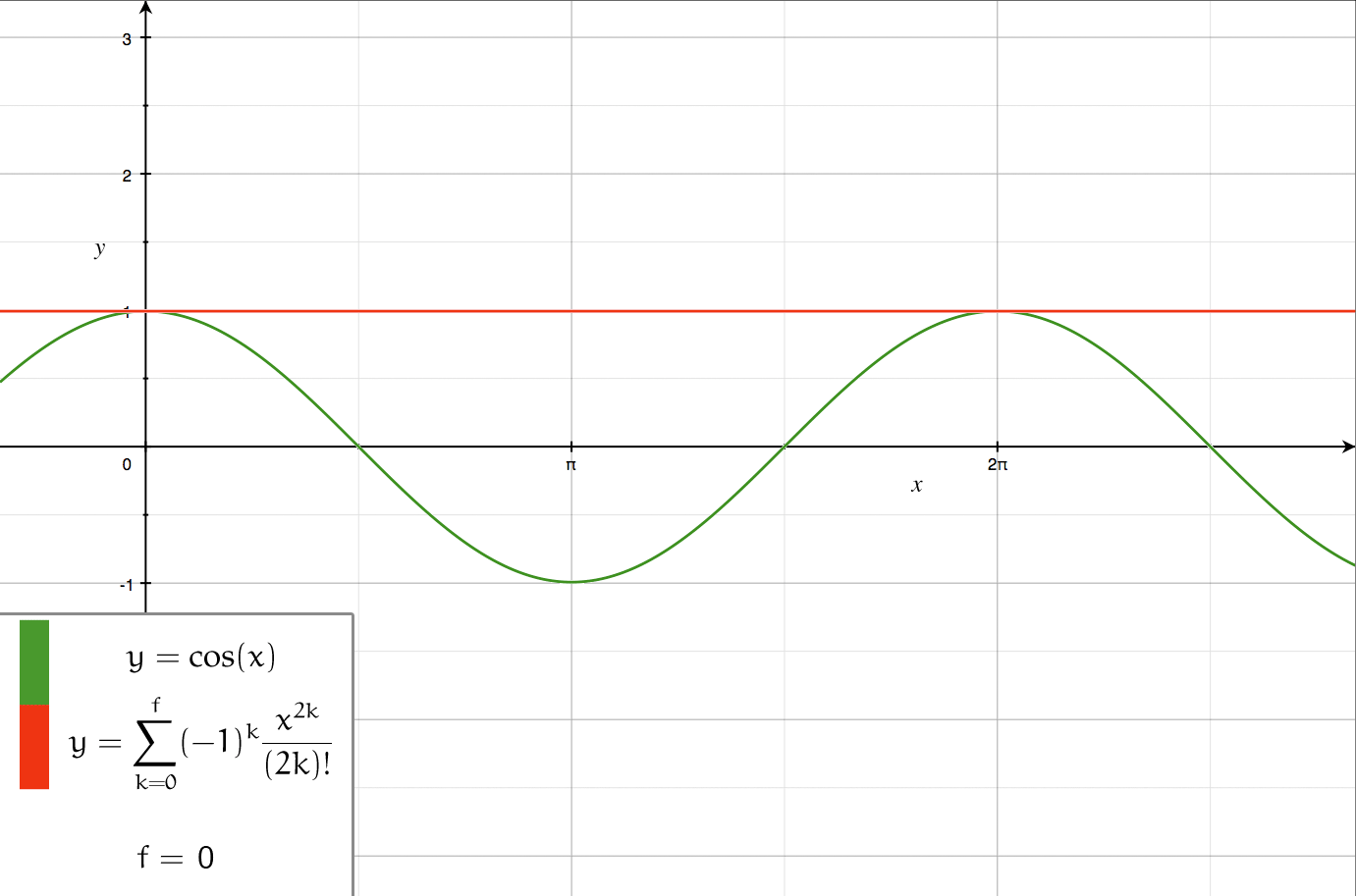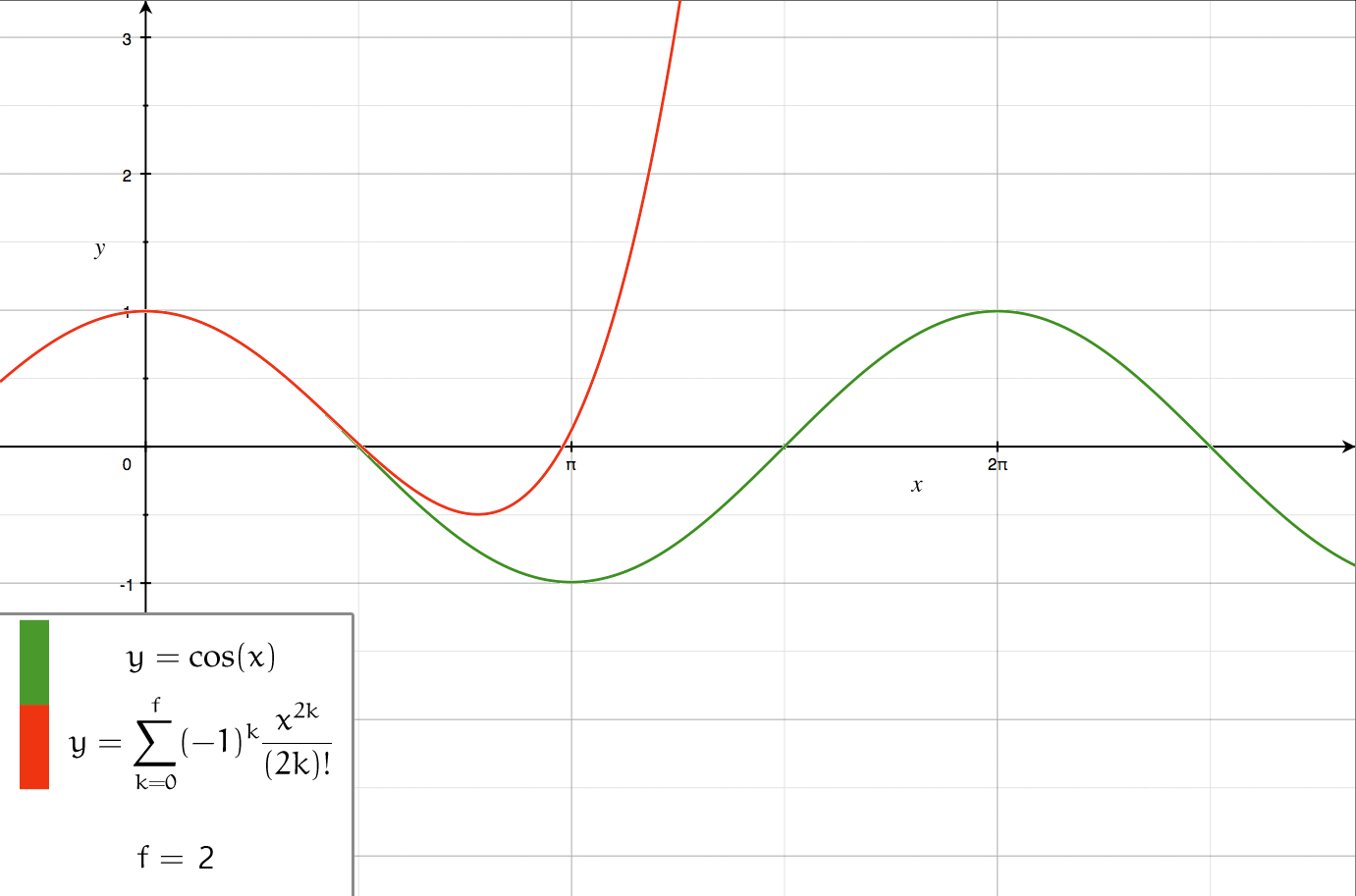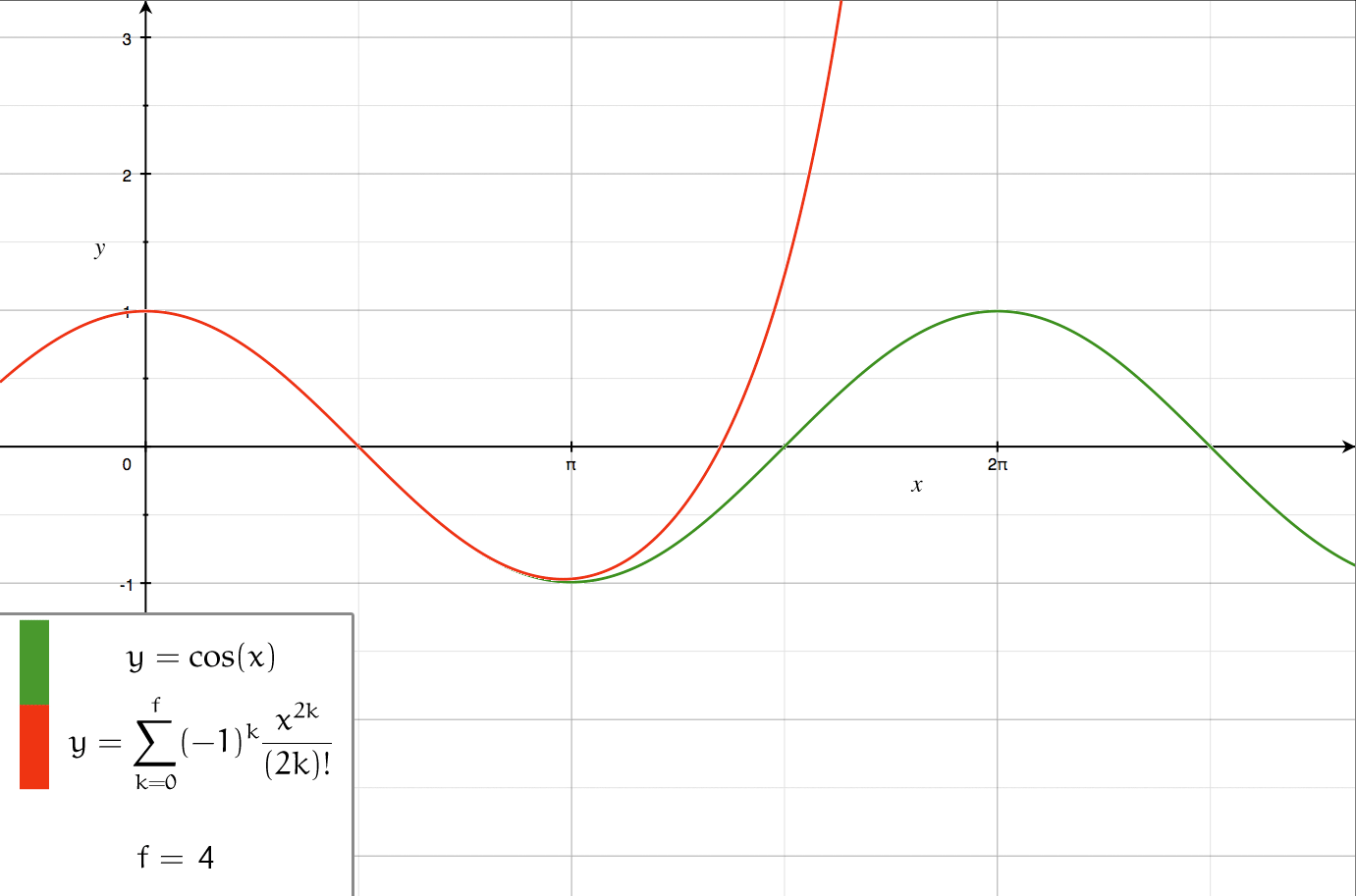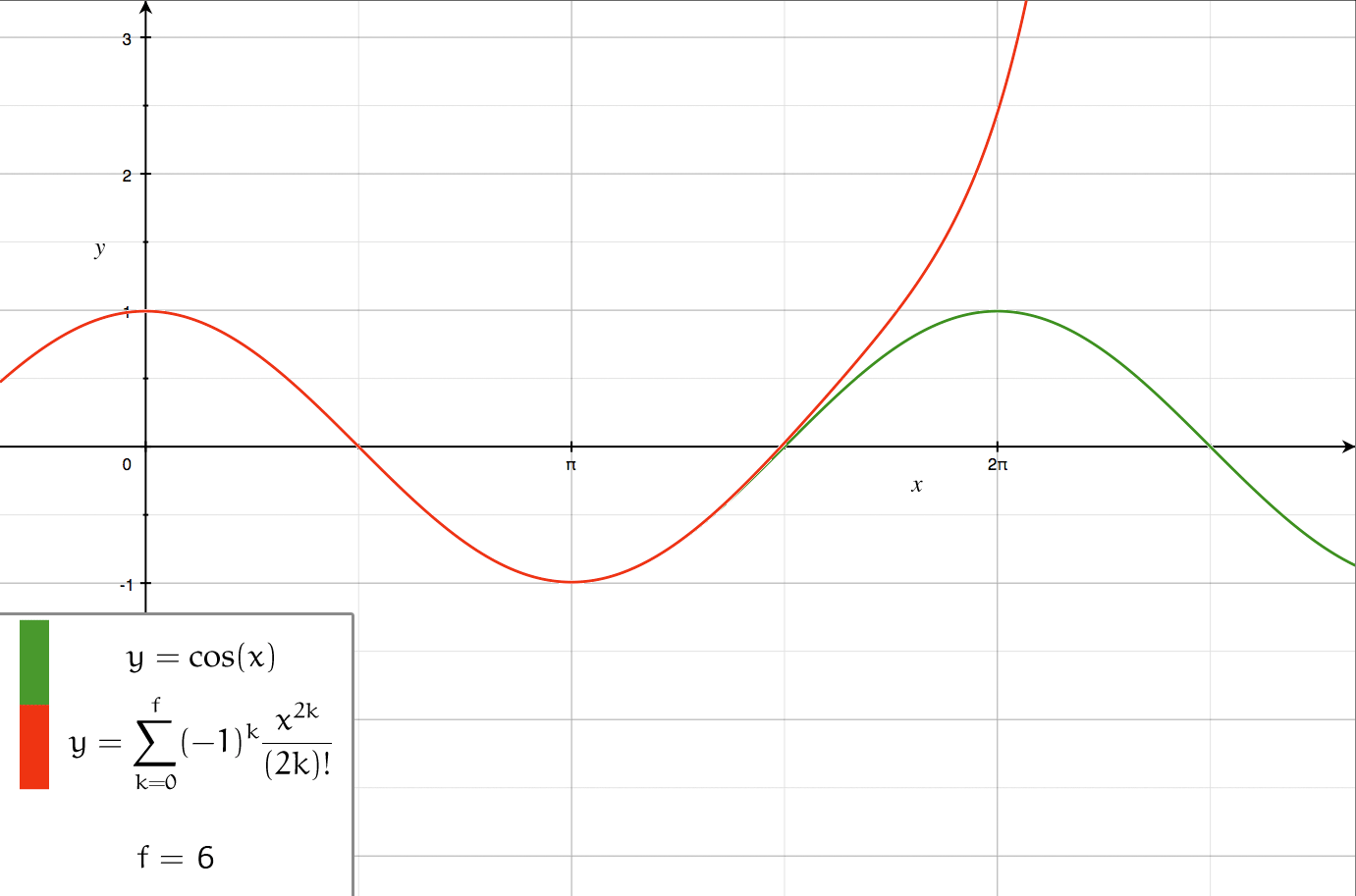
Axial multipole moments are a series expansion of the electric potential of a charge distribution localized close to the origin along one Cartesian axis, denoted here as the ''z''-axis. However, the axial multipole expansion can also be applied to any potential or field that varies inversely with the distance to the source, i.e., as \frac. For clarity, we first illustrate the expansion for a single point charge, then generalize to an arbitrary charge density \lambda(z) localized to the ''z''-axis. Axial multipole moments of a point charge The electric potential of a point charge ''q'' located on the ''z''-axis at z=a (Fig. 1) equals \Phi(\mathbf) = \frac \frac = \frac \frac. If the radius ''r'' of the observation point is greater than ''a'', we may factor out \frac and expand the square root in powers of (a/r)<1 using |
Series Expansion
In mathematics, a series expansion is a technique that expresses a Function (mathematics), function as an infinite sum, or Series (mathematics), series, of simpler functions. It is a method for calculating a Function (mathematics), function that cannot be expressed by just elementary operators (addition, subtraction, multiplication and division). The resulting so-called ''Series (mathematics), series'' often can be limited to a finite number of terms, thus yielding an approximation of the function. The fewer terms of the sequence are used, the simpler this approximation will be. Often, the resulting inaccuracy (i.e., the partial sum of the omitted terms) can be described by an equation involving Big O notation (see also asymptotic expansion). The series expansion on an open interval will also be an approximation for non-analytic functions. Types of series expansions There are several kinds of series expansions, listed below. Taylor series A ''Taylor series'' is a power ser ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Infinitesimal
In mathematics, an infinitesimal number is a non-zero quantity that is closer to 0 than any non-zero real number is. The word ''infinitesimal'' comes from a 17th-century Modern Latin coinage ''infinitesimus'', which originally referred to the "infinity- th" item in a sequence. Infinitesimals do not exist in the standard real number system, but they do exist in other number systems, such as the surreal number system and the hyperreal number system, which can be thought of as the real numbers augmented with both infinitesimal and infinite quantities; the augmentations are the reciprocals of one another. Infinitesimal numbers were introduced in the development of calculus, in which the derivative was first conceived as a ratio of two infinitesimal quantities. This definition was not rigorously formalized. As calculus developed further, infinitesimals were replaced by limits, which can be calculated using the standard real numbers. In the 3rd century BC Archimedes used what ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Laplace Expansion (potential)
In physics, the Laplace expansion of potentials that are directly proportional to the inverse of the distance (1 / r ), such as Newton's law of universal gravitation#Gravity field, Newton's gravitational potential or Coulomb's law#Table of derived quantities, Coulomb's electrostatic potential, expresses them in terms of the spherical Legendre polynomials. In quantum mechanical calculations on atoms the expansion is used in the evaluation of integrals of the inter-electronic repulsion. Formulation The Laplace expansion is in fact the expansion of the inverse distance between two points. Let the points have position vectors \textbf and \textbf' , then the Laplace expansion is \frac = \sum_^\infty \frac \sum_^ (-1)^m \frac Y^_\ell(\theta, \varphi) Y^m_\ell(\theta', \varphi'). Here \textbf has the spherical polar coordinates (r, \theta, \varphi) and \textbf' has (r', \theta', \varphi') with homogeneous polynomials of degree \ell . Further ''r''< is min(''r'', ''r''′) an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Solid Harmonics
In physics and mathematics, the solid harmonics are solutions of the Laplace equation in spherical polar coordinates, assumed to be (smooth) functions \mathbb^3 \to \mathbb. There are two kinds: the ''regular solid harmonics'' R^m_\ell(\mathbf), which are well-defined at the origin and the ''irregular solid harmonics'' I^m_(\mathbf), which are singular at the origin. Both sets of functions play an important role in potential theory, and are obtained by rescaling spherical harmonics appropriately: R^m_(\mathbf) \equiv \sqrt\; r^\ell Y^m_(\theta,\varphi) I^m_(\mathbf) \equiv \sqrt \; \frac Derivation, relation to spherical harmonics Introducing , , and for the spherical polar coordinates of the 3-vector , and assuming that \Phi is a (smooth) function \mathbb^3 \to \mathbb, we can write the Laplace equation in the following form \nabla^2\Phi(\mathbf) = \left(\frac \fracr - \frac\right)\Phi(\mathbf) = 0 , \qquad \mathbf \ne \mathbf, where is the square of the angular moment ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cylindrical Multipole Moments
Cylindrical multipole moments are the coefficients in a series expansion of a potential that varies logarithmically with the distance to a source, i.e., as \ln \ R. Such potentials arise in the electric potential of long line charges, and the analogous sources for the magnetic potential and gravitational potential. For clarity, we illustrate the expansion for a single line charge, then generalize to an arbitrary distribution of line charges. Through this article, the primed coordinates such as (\rho^, \theta^) refer to the position of the line charge(s), whereas the unprimed coordinates such as (\rho, \theta) refer to the point at which the potential is being observed. We use cylindrical coordinates throughout, e.g., an arbitrary vector \mathbf has coordinates ( \rho, \theta, z) where \rho is the radius from the z axis, \theta is the azimuthal angle and z is the normal Cartesian coordinate. By assumption, the line charges are infinitely long and aligned with the z axis. Cylind ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spherical Multipole Moments
In physics, spherical multipole moments are the coefficients in a series expansion of a potential that varies inversely with the distance to a source, ''i.e.'', as Examples of such potentials are the electric potential, the magnetic potential and the gravitational potential. For clarity, we illustrate the expansion for a point charge, then generalize to an arbitrary charge density \rho(\mathbf r'). Through this article, the primed coordinates such as \mathbf r' refer to the position of charge(s), whereas the unprimed coordinates such as \mathbf refer to the point at which the potential is being observed. We also use spherical coordinates throughout, e.g., the vector \mathbf r' has coordinates ( r', \theta', \phi') where r' is the radius, \theta' is the colatitude and \phi' is the azimuthal angle. Spherical multipole moments of a point charge The electric potential due to a point charge located at \mathbf is given by \Phi(\mathbf) = \frac \frac = \frac \frac. where ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multipole Expansion
A multipole expansion is a mathematical series representing a function that depends on angles—usually the two angles used in the spherical coordinate system (the polar and azimuthal angles) for three-dimensional Euclidean space, \R^3. Multipole expansions are useful because, similar to Taylor series, oftentimes only the first few terms are needed to provide a good approximation of the original function. The function being expanded may be real- or complex-valued and is defined either on \R^3, or less often on \R^n for some other Multipole expansions are used frequently in the study of electromagnetic and gravitational fields, where the fields at distant points are given in terms of sources in a small region. The multipole expansion with angles is often combined with an expansion in radius. Such a combination gives an expansion describing a function throughout three-dimensional space. The multipole expansion is expressed as a sum of terms with progressively finer angular f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Potential Theory
In mathematics and mathematical physics, potential theory is the study of harmonic functions. The term "potential theory" was coined in 19th-century physics when it was realized that the two fundamental forces of nature known at the time, namely gravity and the electrostatic force, could be modeled using functions called the gravitational potential and electrostatic potential, both of which satisfy Poisson's equation—or in the vacuum, Laplace's equation. There is considerable overlap between potential theory and the theory of Poisson's equation to the extent that it is impossible to draw a distinction between these two fields. The difference is more one of emphasis than subject matter and rests on the following distinction: potential theory focuses on the properties of the functions as opposed to the properties of the equation. For example, a result about the Mathematical singularity, singularities of harmonic functions would be said to belong to potential theory whilst a result ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electric Charge
Electric charge (symbol ''q'', sometimes ''Q'') is a physical property of matter that causes it to experience a force when placed in an electromagnetic field. Electric charge can be ''positive'' or ''negative''. Like charges repel each other and unlike charges attract each other. An object with no net charge is referred to as neutral particle, electrically neutral. Early knowledge of how charged substances interact is now called classical electrodynamics, and is still accurate for problems that do not require consideration of quantum mechanics, quantum effects. In an isolated system, the total charge stays the same - the amount of positive charge minus the amount of negative charge does not change over time. Electric charge is carried by subatomic particles. In ordinary matter, negative charge is carried by electrons, and positive charge is carried by the protons in the atomic nucleus, nuclei of atoms. If there are more electrons than protons in a piece of matter, it will have a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Charge Density
In electromagnetism, charge density is the amount of electric charge per unit length, surface area, or volume. Volume charge density (symbolized by the Greek letter ρ) is the quantity of charge per unit volume, measured in the SI system in coulombs per cubic meter (C⋅m−3), at any point in a volume. Surface charge density (σ) is the quantity of charge per unit area, measured in coulombs per square meter (C⋅m−2), at any point on a surface charge distribution on a two dimensional surface. Linear charge density (λ) is the quantity of charge per unit length, measured in coulombs per meter (C⋅m−1), at any point on a line charge distribution. Charge density can be either positive or negative, since electric charge can be either positive or negative. Like mass density, charge density can vary with position. In classical electromagnetic theory charge density is idealized as a '' continuous'' scalar function of position \boldsymbol, like a fluid, and \rho(\boldsymbo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coordinate System
In geometry, a coordinate system is a system that uses one or more numbers, or coordinates, to uniquely determine and standardize the position of the points or other geometric elements on a manifold such as Euclidean space. The coordinates are not interchangeable; they are commonly distinguished by their position in an ordered tuple, or by a label, such as in "the ''x''-coordinate". The coordinates are taken to be real numbers in elementary mathematics, but may be complex numbers or elements of a more abstract system such as a commutative ring. The use of a coordinate system allows problems in geometry to be translated into problems about numbers and ''vice versa''; this is the basis of analytic geometry. Common coordinate systems Number line The simplest example of a coordinate system is the identification of points on a line with real numbers using the '' number line''. In this system, an arbitrary point ''O'' (the ''origin'') is chosen on a given line. The coordinate o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electric Potential
Electric potential (also called the ''electric field potential'', potential drop, the electrostatic potential) is defined as electric potential energy per unit of electric charge. More precisely, electric potential is the amount of work (physics), work needed to move a test charge from a reference point to a specific point in a static electric field. The test charge used is small enough that disturbance to the field is unnoticeable, and its motion across the field is supposed to proceed with negligible acceleration, so as to avoid the test charge acquiring kinetic energy or producing radiation. By definition, the electric potential at the reference point is zero units. Typically, the reference point is Earth (electricity), earth or a point at infinity, although any point can be used. In classical electrostatics, the electrostatic field is a vector quantity expressed as the gradient of the electrostatic potential, which is a scalar (physics), scalar quantity denoted by or occasi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |