|
Arnold Diffusion
In applied mathematics, Arnold diffusion is the phenomenon of instability of nearly-integrable systems, integrable Hamiltonian systems. The phenomenon is named after Vladimir Arnold who was the first to publish a result in the field in 1964. More precisely, Arnold diffusion refers to results asserting the existence of solutions to nearly-integrable Hamiltonian systems that exhibit a significant change in the action variables. Arnold diffusion describes the diffusion of trajectories due to the ergodic theorem in a portion of phase space unbound by any constraints (''i.e.'' unbounded by action-angle variables, Lagrangian tori arising from constants of motion) in Hamiltonian systems. It occurs in systems with more than ''N''=2 degrees of freedom, since the ''N''-dimensional invariant tori do not separate the 2''N''-1 dimensional phase space any more. Thus, an arbitrarily small perturbation may cause a number of trajectories to wander pseudo-randomly through the whole portion of phase ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Applied Mathematics
Applied mathematics is the application of mathematics, mathematical methods by different fields such as physics, engineering, medicine, biology, finance, business, computer science, and Industrial sector, industry. Thus, applied mathematics is a combination of mathematical science and specialized knowledge. The term "applied mathematics" also describes the profession, professional specialty in which mathematicians work on practical problems by formulating and studying mathematical models. In the past, practical applications have motivated the development of mathematical theories, which then became the subject of study in pure mathematics where abstract concepts are studied for their own sake. The activity of applied mathematics is thus intimately connected with research in pure mathematics. History Historically, applied mathematics consisted principally of Mathematical analysis, applied analysis, most notably differential equations; approximation theory (broadly construed, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integrable Systems
In mathematics, integrability is a property of certain dynamical systems. While there are several distinct formal definitions, informally speaking, an integrable system is a dynamical system with sufficiently many conserved quantities, or first integrals, that its motion is confined to a submanifold of much smaller dimensionality than that of its phase space. Three features are often referred to as characterizing integrable systems: * the existence of a ''maximal'' set of conserved quantities (the usual defining property of complete integrability) * the existence of algebraic invariants, having a basis in algebraic geometry (a property known sometimes as algebraic integrability) * the explicit determination of solutions in an explicit functional form (not an intrinsic property, but something often referred to as solvability) Integrable systems may be seen as very different in qualitative character from more ''generic'' dynamical systems, which are more typically chaotic syste ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hamiltonian System
A Hamiltonian system is a dynamical system governed by Hamilton's equations. In physics, this dynamical system describes the evolution of a physical system such as a planetary system or an electron in an electromagnetic field. These systems can be studied in both Hamiltonian mechanics and dynamical systems theory. Overview Informally, a Hamiltonian system is a mathematical formalism developed by William Rowan Hamilton, Hamilton to describe the evolution equation, evolution equations of a physical system. The advantage of this description is that it gives important insights into the dynamics, even if the initial value problem cannot be solved analytically. One example is the Three-body problem, planetary movement of three bodies: while there is no closed-form solution to the general problem, Henri Poincaré, Poincaré showed for the first time that it exhibits deterministic chaos. Formally, a Hamiltonian system is a dynamical system characterised by the scalar function H(\bol ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vladimir Arnold
Vladimir Igorevich Arnold (or Arnol'd; , ; 12 June 1937 – 3 June 2010) was a Soviet and Russian mathematician. He is best known for the Kolmogorov–Arnold–Moser theorem regarding the stability of integrable systems, and contributed to several areas, including geometrical theory of dynamical systems, algebra, catastrophe theory, topology, real algebraic geometry, symplectic geometry, differential equations, classical mechanics, differential-geometric approach to hydrodynamics, geometric analysis and singularity theory, including posing the ADE classification problem. His first main result was the solution of Hilbert's thirteenth problem in 1957 when he was 19. He co-founded three new branches of mathematics: topological Galois theory (with his student Askold Khovanskii), symplectic topology and KAM theory. Arnold was also a populariser of mathematics. Through his lectures, seminars, and as the author of several textbooks (such as '' Mathematical Methods of Clas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Soviet Mathematics
The ''Proceedings of the USSR Academy of Sciences'' (, ''Doklady Akademii Nauk SSSR'' (''DAN SSSR''), ) was a Soviet journal that was dedicated to publishing original, academic research papers in physics, mathematics, chemistry, geology, and biology. It was first published in 1933 and ended in 1992 with volume 322, issue 3. Today, it is continued by ''Doklady Akademii Nauk'' (), which began publication in 1992. The journal is also known as the ''Proceedings of the Russian Academy of Sciences (RAS)''. ''Doklady'' has had a complicated publication and translation history. A number of translation journals exist which publish selected articles from the original by subject section; these are listed below. The journal is indexed in Russian Science Citation Index. History The Russian Academy of Sciences dates from 1724, with a continuous series of variously named publications dating from 1726. ''Doklady Akademii Nauk SSSR-Comptes Rendus de l'Académie des Sciences de l'URSS, Seriya A ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ergodic Theorem
Ergodic theory is a branch of mathematics that studies statistical properties of deterministic dynamical systems; it is the study of ergodicity. In this context, "statistical properties" refers to properties which are expressed through the behavior of time averages of various functions along trajectories of dynamical systems. The notion of deterministic dynamical systems assumes that the equations determining the dynamics do not contain any random perturbations, noise, etc. Thus, the statistics with which we are concerned are properties of the dynamics. Ergodic theory, like probability theory, is based on general notions of measure theory. Its initial development was motivated by problems of statistical physics. A central concern of ergodic theory is the behavior of a dynamical system when it is allowed to run for a long time. The first result in this direction is the Poincaré recurrence theorem, which claims that almost all points in any subset of the phase space eventuall ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
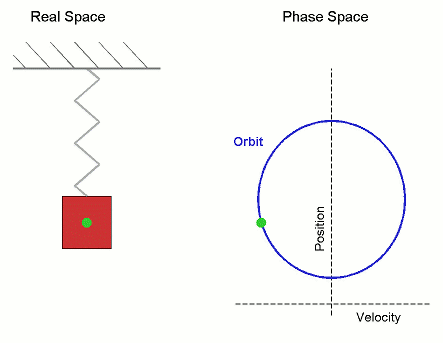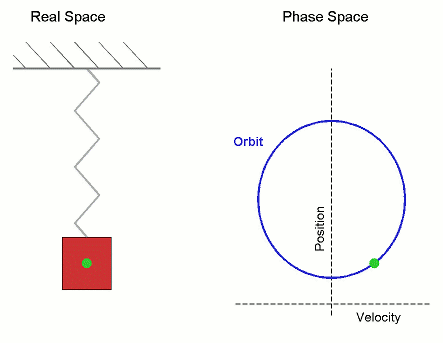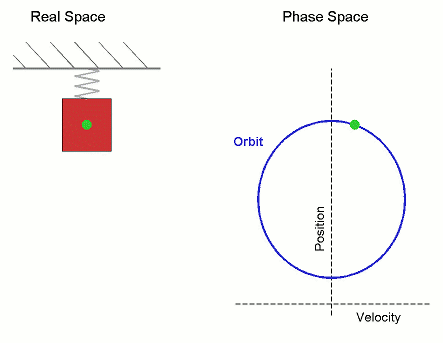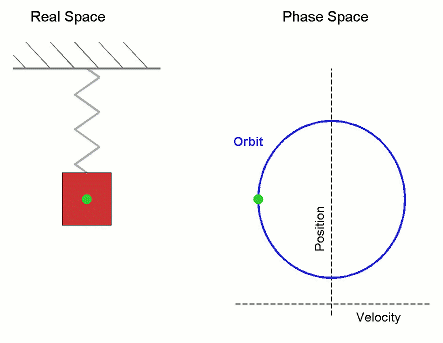
Phase Space
The phase space of a physical system is the set of all possible physical states of the system when described by a given parameterization. Each possible state corresponds uniquely to a point in the phase space. For mechanical systems, the phase space usually consists of all possible values of the position and momentum parameters. It is the direct product of direct space and reciprocal space. The concept of phase space was developed in the late 19th century by Ludwig Boltzmann, Henri Poincaré, and Josiah Willard Gibbs. Principles In a phase space, every degree of freedom or parameter of the system is represented as an axis of a multidimensional space; a one-dimensional system is called a phase line, while a two-dimensional system is called a phase plane. For every possible state of the system or allowed combination of values of the system's parameters, a point is included in the multidimensional space. The system's evolving state over time traces a path (a phase-spac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Action-angle Variables
In classical mechanics, action-angle variables are a set of canonical coordinates that are useful in characterizing the nature of commuting flows in integrable systems when the conserved energy level set is compact, and the commuting flows are complete. Action-angle variables are also important in obtaining the frequencies of oscillatory or rotational motion without solving the equations of motion. They only exist, providing a key characterization of the dynamics, when the system is completely integrable, i.e., the number of independent Poisson commuting invariants is maximal and the conserved energy surface is compact. This is usually of practical calculational value when the Hamilton–Jacobi equation is completely separable, and the separation constants can be solved for, as functions on the phase space. Action-angle variables define a foliation by invariant Lagrangian tori because the flows induced by the Poisson commuting invariants remain within their joint level sets, whil ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Constants Of Motion
In mechanics, a constant of motion is a physical quantity conserved throughout the motion, imposing in effect a constraint on the motion. However, it is a ''mathematical'' constraint, the natural consequence of the equations of motion, rather than a ''physical'' constraint (which would require extra constraint forces). Common examples include energy, linear momentum, angular momentum and the Laplace–Runge–Lenz vector (for inverse-square force laws). Applications Constants of motion are useful because they allow properties of the motion to be derived without solving the equations of motion. In fortunate cases, even the trajectory of the motion can be derived as the intersection of isosurfaces corresponding to the constants of motion. For example, Poinsot's construction shows that the torque-free rotation of a rigid body is the intersection of a sphere (conservation of total angular momentum) and an ellipsoid (conservation of energy), a trajectory that might be otherwis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
KAM Theorem
Kaam ( Punjabi: ਕਾਮ; ''Kāma'') is one of the five thieves in Sikhism, described as excessive lust or desire. A devout Sikh is expected to be in control of ''Kaam'' at all times. Translation The term has been rendered as translating to desire, longing, concupiscence, sensuality or lasciviousness in English. Description In common parlance, the term refers to excessive sexual desire. Sikhism views kaam as an urge that an individual must keep in-control from time to time. It is not viewed as dissimilar to other urges and cravings of the human experience that must also be periodically kept in-check. Kaam becomes a true evil when it begins interfering with one's marital life, such as leading a spouse to cheat on their partner under its influence. Sikhism condemns kaam which interferes with the spiritual journey and day-to-day life of an individual. Guru Tegh Bahadur states the following on the issue of kaam: The word refers to all desires but usually it is used in refe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Unstable Manifold
In mathematics, and in particular the study of dynamical systems, the idea of ''stable and unstable sets'' or stable and unstable manifolds give a formal mathematical definition to the general notions embodied in the idea of an attractor or repellor. In the case of hyperbolic dynamics, the corresponding notion is that of the hyperbolic set. Physical example The gravitational tidal forces acting on the rings of Saturn provide an easy-to-visualize physical example. The tidal forces flatten the ring into the equatorial plane, even as they stretch it out in the radial direction. Imagining the rings to be sand or gravel particles ("dust") in orbit around Saturn, the tidal forces are such that any perturbations that push particles above or below the equatorial plane results in that particle feeling a restoring force, pushing it back into the plane. Particles effectively oscillate in a harmonic well, damped by collisions. The stable direction is perpendicular to the ring. The unstable ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |