|
Apse Line
An apse line, or line of apsides, is an imaginary line defined by an orbit's eccentricity vector. It is strictly defined for elliptic, parabolic, and hyperbolic orbits. For such orbits the apse line is found: * for elliptical orbitsbetween the orbit's periapsis and apoapsis (also known as the major axis) * for parabolic and hyperbolic orbitsbetween the orbit's periapsis and focus For circular orbits, the apse line is not defined because the eccentricity is equal to zero. As it is required as a base for the definition of true anomaly, it is usually arbitrarily assumed (as a line pointing into the direction of the vernal equinox). See also * Apsidal precession * Apsis * Eccentricity (orbit) * Orbit: circular, elliptic, parabolic and hyperbolic * True anomaly In celestial mechanics, true anomaly is an angular parameter that defines the position of a body moving along a Keplerian orbit. It is the angle between the direction of periapsis and the current position of the body, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Apogee (PSF) Mul
An apsis (; ) is the farthest or nearest point in the orbit of a planetary body about its primary body. The line of apsides (also called apse line, or major axis of the orbit) is the line connecting the two extreme values. Apsides pertaining to orbits around different bodies have distinct names to differentiate themselves from other apsides. Apsides pertaining to geocentric orbits, orbits around the Earth, are at the farthest point called the ''apogee'', and at the nearest point the ''perigee'', like with orbits of satellites and the Moon around Earth. Apsides pertaining to orbits around the Sun are named ''aphelion'' for the farthest and ''perihelion'' for the nearest point in a heliocentric orbit. Earth's two apsides are the farthest point, ''aphelion'', and the nearest point, ''perihelion'', of its orbit around the host Sun. The terms ''aphelion'' and ''perihelion'' apply in the same way to the orbits of Jupiter and the other planets, the comets, and the asteroids ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circular Orbit
A circular orbit is an orbit with a fixed distance around the barycenter; that is, in the shape of a circle. In this case, not only the distance, but also the speed, angular speed, Potential energy, potential and kinetic energy are constant. There is no periapsis or apoapsis. This orbit has no Radial orbit, radial version. Listed below is a circular orbit in astrodynamics or celestial mechanics under standard assumptions. Here the centripetal force is the gravitational force, and the axis mentioned above is the line through the Center of mass, center of the central mass perpendicular to the orbital plane. Circular acceleration :wikt:transverse, Transverse acceleration (perpendicular to velocity) causes a change in direction. If it is constant in magnitude and changing in direction with the velocity, circular motion ensues. Taking two derivatives of the particle's coordinates concerning time gives the centripetal acceleration : a\, = \frac \, = where: *v\, is Kinetic e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orbit
In celestial mechanics, an orbit (also known as orbital revolution) is the curved trajectory of an object such as the trajectory of a planet around a star, or of a natural satellite around a planet, or of an artificial satellite around an object or position in space such as a planet, moon, asteroid, or Lagrange point. Normally, orbit refers to a regularly repeating trajectory, although it may also refer to a non-repeating trajectory. To a close approximation, planets and satellites follow elliptic orbits, with the center of mass being orbited at a focal point of the ellipse, as described by Kepler's laws of planetary motion. For most situations, orbital motion is adequately approximated by Newtonian mechanics, which explains gravity as a force obeying an inverse-square law. However, Albert Einstein's general theory of relativity, which accounts for gravity as due to curvature of spacetime, with orbits following geodesics, provides a more accurate calculation and u ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
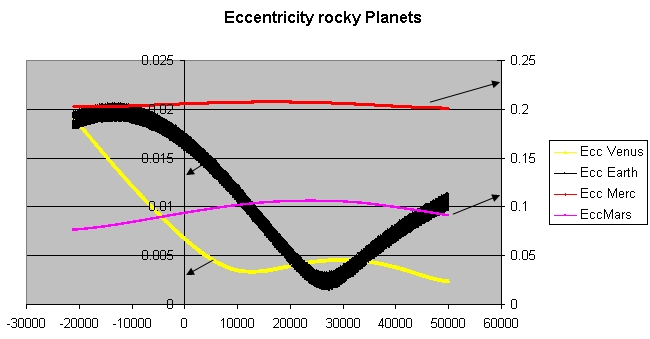
Eccentricity (orbit)
In astrodynamics, the orbital eccentricity of an astronomical object is a dimensionless parameter that determines the amount by which its orbit around another body deviates from a perfect circle. A value of 0 is a circular orbit, values between 0 and 1 form an elliptic orbit, 1 is a parabolic escape orbit (or capture orbit), and greater than 1 is a hyperbola. The term derives its name from the parameters of conic sections, as every Kepler orbit is a conic section. It is normally used for the isolated two-body problem, but extensions exist for objects following a rosette orbit through the Galaxy. Definition In a two-body problem with inverse-square-law force, every orbit is a Kepler orbit. The eccentricity of this Kepler orbit is a non-negative number that defines its shape. The eccentricity may take the following values: * Circular orbit: * Elliptic orbit: * Parabolic trajectory: * Hyperbolic trajectory: The eccentricity is given by e = \sqrt where is the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Apsis
An apsis (; ) is the farthest or nearest point in the orbit of a planetary body about its primary body. The line of apsides (also called apse line, or major axis of the orbit) is the line connecting the two extreme values. Apsides pertaining to orbits around different bodies have distinct names to differentiate themselves from other apsides. Apsides pertaining to geocentric orbits, orbits around the Earth, are at the farthest point called the ''apogee'', and at the nearest point the ''perigee'', like with orbits of satellites and the Moon around Earth. Apsides pertaining to orbits around the Sun are named ''aphelion'' for the farthest and ''perihelion'' for the nearest point in a heliocentric orbit. Earth's two apsides are the farthest point, ''aphelion'', and the nearest point, ''perihelion'', of its orbit around the host Sun. The terms ''aphelion'' and ''perihelion'' apply in the same way to the orbits of Jupiter and the other planets, the comets, and the asteroids of t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
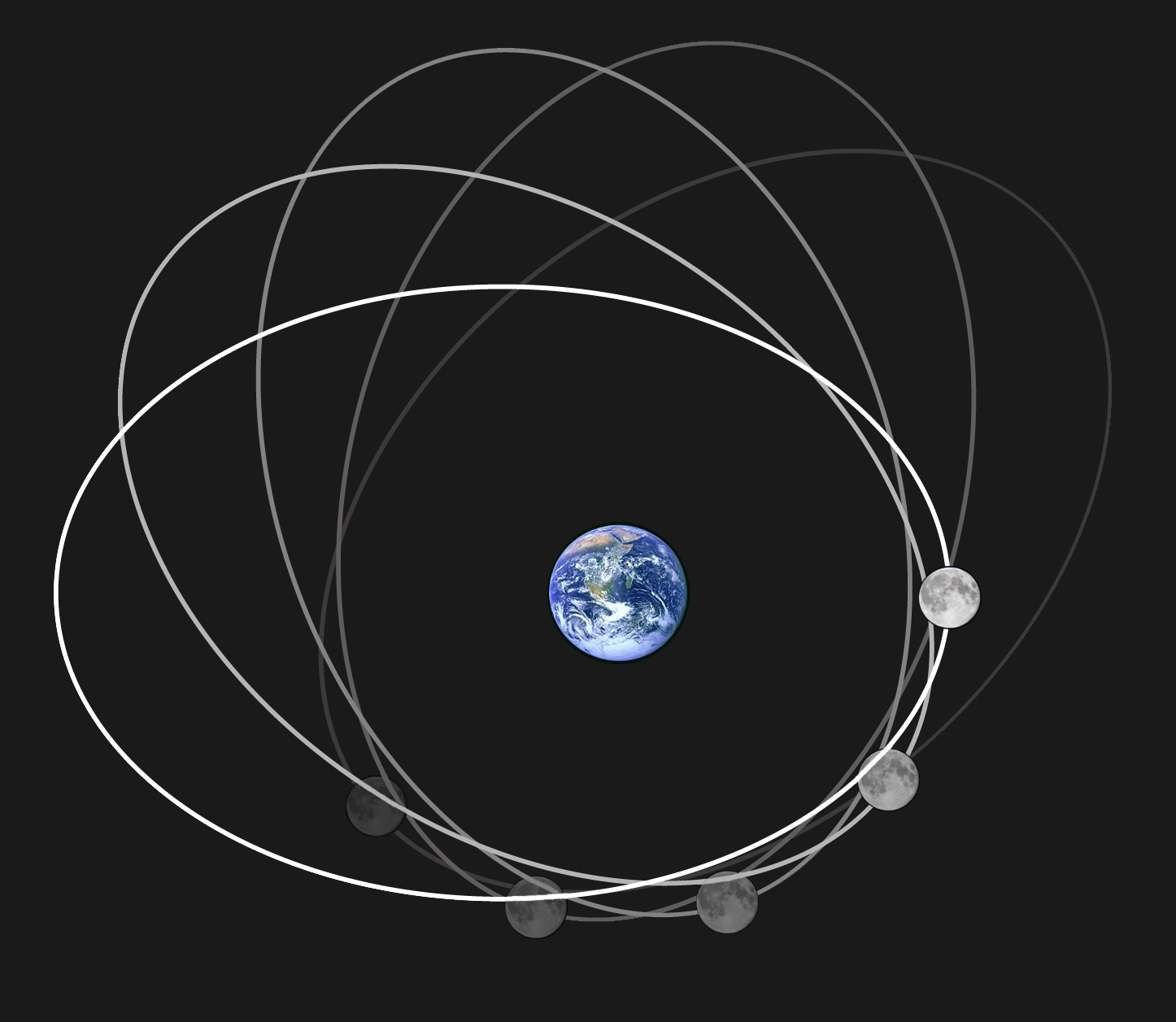
Apsidal Precession
In celestial mechanics, apsidal precession (or apsidal advance) is the precession (gradual rotation) of the line connecting the apsis, apsides (line of apsides) of an orbiting body, astronomical body's orbit. The apsides are the orbital points farthest (apoapsis) and closest (periapsis) from its primary (astronomy), primary body. The apsidal precession is the first time derivative of the argument of periapsis, one of the six main orbital elements of an orbit. Apsidal precession is considered positive when the orbit's axis rotates in the same direction as the orbital motion. An apsidal period is the time interval required for an orbit to precess through 360°, which takes the Earth about 112,000 years and the Moon about 8.85 years. History The ancient Greek astronomer Hipparchus noted the apsidal precession of the Moon's orbit (as the revolution of the Moon's apogee with a period of approximately 8.85 years); it is corrected for in the Antikythera Mechanism (circa 80 BC ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equinox
A solar equinox is a moment in time when the Sun appears directly above the equator, rather than to its north or south. On the day of the equinox, the Sun appears to rise directly east and set directly west. This occurs twice each year, around 20 March and 23 September. An equinox is equivalently defined as the time when the plane of Earth's equator passes through the geometric center of the Sun's disk. This is also the moment when Earth's rotation axis is directly perpendicular to the Sun-Earth line, tilting neither toward nor away from the Sun. In modern times, since the Moon (and to a lesser extent the planets) causes Earth's orbit to vary slightly from a perfect ellipse, the equinox is officially defined by the Sun's more regular ecliptic longitude rather than by its declination. The instants of the equinoxes are currently defined to be when the apparent geocentric longitude of the Sun is 0° and 180°. The word is derived from the Latin ', from ' (equal) and ' ( ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
True Anomaly
In celestial mechanics, true anomaly is an angular parameter that defines the position of a body moving along a Keplerian orbit. It is the angle between the direction of periapsis and the current position of the body, as seen from the main focus of the ellipse (the point around which the object orbits). The true anomaly is usually denoted by the Greek alphabet, Greek letters or , or the Latin script, Latin letter , and is usually restricted to the range 0–360° (0–2π rad). The true anomaly is one of three angular parameters (''anomalies'') that can be used to define a position along an orbit, the other three being the eccentric anomaly and the mean anomaly. Formulas From state vectors For elliptic orbits, the true anomaly can be calculated from orbital state vectors as: : \nu = \arccos ::(if then replace by ) where: * v is the orbital velocity vector of the orbiting body, * e is the eccentricity vector, * r is the orbital position vector (segment ''FP'' in the fi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orbital Eccentricity
In astrodynamics, the orbital eccentricity of an astronomical object is a dimensionless parameter that determines the amount by which its orbit around another body deviates from a perfect circle. A value of 0 is a circular orbit, values between 0 and 1 form an elliptic orbit, 1 is a parabolic escape orbit (or capture orbit), and greater than 1 is a hyperbola. The term derives its name from the parameters of conic sections, as every Kepler orbit is a conic section. It is normally used for the isolated two-body problem, but extensions exist for objects following a rosette orbit through the Galaxy. Definition In a two-body problem with inverse-square-law force, every orbit is a Kepler orbit. The eccentricity of this Kepler orbit is a non-negative number that defines its shape. The eccentricity may take the following values: * Circular orbit: * Elliptic orbit: * Parabolic trajectory: * Hyperbolic trajectory: The eccentricity is given by e = \sqrt where ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Focus (geometry)
In geometry, focuses or foci (; : focus) are special points with reference to which any of a variety of curves is constructed. For example, one or two foci can be used in defining conic sections, the four types of which are the circle, ellipse, parabola, and hyperbola. In addition, two foci are used to define the Cassini oval and the Cartesian oval, and more than two foci are used in defining an n-ellipse, ''n''-ellipse. Conic sections Defining conics in terms of two foci An ellipse can be defined as the locus (mathematics), locus of points for which the sum of the distances to two given foci is constant. A circle is the special case of an ellipse in which the two foci coincide with each other. Thus, a circle can be more simply defined as the locus of points each of which is a fixed distance from a single given focus. A circle can also be defined as the Circles of Apollonius, circle of Apollonius, in terms of two different foci, as the locus of points having a fixed ratio of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orbit
In celestial mechanics, an orbit (also known as orbital revolution) is the curved trajectory of an object such as the trajectory of a planet around a star, or of a natural satellite around a planet, or of an artificial satellite around an object or position in space such as a planet, moon, asteroid, or Lagrange point. Normally, orbit refers to a regularly repeating trajectory, although it may also refer to a non-repeating trajectory. To a close approximation, planets and satellites follow elliptic orbits, with the center of mass being orbited at a focal point of the ellipse, as described by Kepler's laws of planetary motion. For most situations, orbital motion is adequately approximated by Newtonian mechanics, which explains gravity as a force obeying an inverse-square law. However, Albert Einstein's general theory of relativity, which accounts for gravity as due to curvature of spacetime, with orbits following geodesics, provides a more accurate calculation and u ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |