|
Algebraic Semantics (computer Science)
In computer science, algebraic semantics is a formal approach to programming language theory that uses algebraic methods for defining, specifying, and reasoning about the behavior of programs. It is a form of axiomatic semantics that provides a mathematical framework for analyzing programs through the use of algebraic structures and equational logic. Algebraic semantics represents programs and data types as algebras—mathematical structures consisting of sets equipped with operations that satisfy certain equational laws. This approach enables rigorous formal verification of software by treating program properties as algebraic properties that can be proven through mathematical reasoning. A key advantage of algebraic semantics is its ability to separate the specification of what a program does from how it is implemented, supporting abstraction and modularity in software design. Syntax The syntax of an algebraic specification is formulated in two steps: (1) defining a form ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computer Science
Computer science is the study of computation, information, and automation. Computer science spans Theoretical computer science, theoretical disciplines (such as algorithms, theory of computation, and information theory) to Applied science, applied disciplines (including the design and implementation of Computer architecture, hardware and Software engineering, software). Algorithms and data structures are central to computer science. The theory of computation concerns abstract models of computation and general classes of computational problem, problems that can be solved using them. The fields of cryptography and computer security involve studying the means for secure communication and preventing security vulnerabilities. Computer graphics (computer science), Computer graphics and computational geometry address the generation of images. Programming language theory considers different ways to describe computational processes, and database theory concerns the management of re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Modularity
Modularity is the degree to which a system's components may be separated and recombined, often with the benefit of flexibility and variety in use. The concept of modularity is used primarily to reduce complexity by breaking a system into varying degrees of interdependence and independence across and "hide the complexity of each part behind an abstraction and interface". However, the concept of modularity can be extended to multiple disciplines, each with their own nuances. Despite these nuances, consistent themes concerning modular systems can be identified. Composability is one of the tenets of functional programming. This makes functional programs modular. Contextual nuances The meaning of the word "modularity" can vary somewhat based on context. The following are contextual examples of modularity across several fields of science, technology, industry, and culture: Science *In biology, modularity recognizes that organisms or metabolic pathways are composed of modules. *I ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Empty String
In formal language theory, the empty string, or empty word, is the unique String (computer science), string of length zero. Formal theory Formally, a string is a finite, ordered sequence of character (symbol), characters such as letters, digits or spaces. The empty string is the special case where the sequence has length zero, so there are no symbols in the string. There is only one empty string, because two strings are only different if they have different lengths or a different sequence of symbols. In formal treatments, the empty string is denoted with ε or sometimes Λ or λ. The empty string should not be confused with the empty language ∅, which is a formal language (i.e. a set of strings) that contains no strings, not even the empty string. The empty string has several properties: * , ε, = 0. Its string (computer science)#Formal theory, string length is zero. * ε ⋅ s = s ⋅ ε = s. The empty string is the identity element of the concatenation operation. The set of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stack (abstract Data Type)
In computer science, a stack is an abstract data type that serves as a collection (abstract data type), collection of elements with two main operations: * Push, which adds an element to the collection, and * Pop, which removes the most recently added element. Additionally, a peek (data type operation), peek operation can, without modifying the stack, return the value of the last element added. The name ''stack'' is an analogy to a set of physical items stacked one atop another, such as a stack of plates. The order in which an element added to or removed from a stack is described as last in, first out, referred to by the acronym LIFO. As with a stack of physical objects, this structure makes it easy to take an item off the top of the stack, but accessing a Data, datum deeper in the stack may require removing multiple other items first. Considered a sequential collection, a stack has one end which is the only position at which the push and pop operations may occur, the ''top'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integer
An integer is the number zero (0), a positive natural number (1, 2, 3, ...), or the negation of a positive natural number (−1, −2, −3, ...). The negations or additive inverses of the positive natural numbers are referred to as negative integers. The set (mathematics), set of all integers is often denoted by the boldface or blackboard bold The set of natural numbers \mathbb is a subset of \mathbb, which in turn is a subset of the set of all rational numbers \mathbb, itself a subset of the real numbers \mathbb. Like the set of natural numbers, the set of integers \mathbb is Countable set, countably infinite. An integer may be regarded as a real number that can be written without a fraction, fractional component. For example, 21, 4, 0, and −2048 are integers, while 9.75, , 5/4, and Square root of 2, are not. The integers form the smallest Group (mathematics), group and the smallest ring (mathematics), ring containing the natural numbers. In algebraic number theory, the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Symbol
A symbol is a mark, Sign (semiotics), sign, or word that indicates, signifies, or is understood as representing an idea, physical object, object, or wikt:relationship, relationship. Symbols allow people to go beyond what is known or seen by creating linkages between otherwise different concepts and experiences. All communication is achieved through the use of symbols: for example, a red octagon is a common symbol for "Stop sign, STOP"; on maps, blue lines often represent rivers; and a red rose often symbolizes love and compassion. Numerical digit, Numerals are symbols for numbers; Letter (alphabet), letters of an alphabet may be symbols for certain phonemes; and personal names are symbols representing individuals. The academic study of symbols is called semiotics. In the arts, Artistic symbol, symbolism is the use of a abstract and concrete, concrete element to represent a more abstract idea. In cartography, an organized collection of symbols forms a map layout, legend for a ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
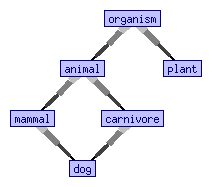
Family Of Sets
In set theory and related branches of mathematics, a family (or collection) can mean, depending upon the context, any of the following: set, indexed set, multiset, or class. A collection F of subsets of a given set S is called a family of subsets of S, or a family of sets over S. More generally, a collection of any sets whatsoever is called a family of sets, set family, or a set system. Additionally, a family of sets may be defined as a function from a set I, known as the index set, to F, in which case the sets of the family are indexed by members of I. In some contexts, a family of sets may be allowed to contain repeated copies of any given member, and in other contexts it may form a proper class. A finite family of subsets of a finite set S is also called a '' hypergraph''. The subject of extremal set theory concerns the largest and smallest examples of families of sets satisfying certain restrictions. Examples The set of all subsets of a given set S is called the pow ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Many-sorted Logic
Many-sorted logic can reflect formally our intention not to handle the universe as a homogeneous collection of objects, but to partition it in a way that is similar to types in typeful programming. Both functional and assertive " parts of speech" in the language of the logic reflect this typeful partitioning of the universe, even on the syntax level: substitution and argument passing can be done only accordingly, respecting the "sorts". There are various ways to formalize the intention mentioned above; a ''many-sorted logic'' is any package of information which fulfils it. In most cases, the following are given: * a set of sorts, ''S'' * an appropriate generalization of the notion of ''signature'' to be able to handle the additional information that comes with the sorts. The domain of discourse of any structure of that signature is then fragmented into disjoint subsets, one for every sort. Example When reasoning about biological organisms, it is useful to distinguish two sorts ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Data Type
In computer science and computer programming, a data type (or simply type) is a collection or grouping of data values, usually specified by a set of possible values, a set of allowed operations on these values, and/or a representation of these values as machine types. A data type specification in a program constrains the possible values that an expression, such as a variable or a function call, might take. On literal data, it tells the compiler or interpreter how the programmer intends to use the data. Most programming languages support basic data types of integer numbers (of varying sizes), floating-point numbers (which approximate real numbers), characters and Booleans. Concept A data type may be specified for many reasons: similarity, convenience, or to focus the attention. It is frequently a matter of good organization that aids the understanding of complex definitions. Almost all programming languages explicitly include the notion of data type, though the possible d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Set (mathematics)
In mathematics, a set is a collection of different things; the things are '' elements'' or ''members'' of the set and are typically mathematical objects: numbers, symbols, points in space, lines, other geometric shapes, variables, or other sets. A set may be finite or infinite. There is a unique set with no elements, called the empty set; a set with a single element is a singleton. Sets are ubiquitous in modern mathematics. Indeed, set theory, more specifically Zermelo–Fraenkel set theory, has been the standard way to provide rigorous foundations for all branches of mathematics since the first half of the 20th century. Context Before the end of the 19th century, sets were not studied specifically, and were not clearly distinguished from sequences. Most mathematicians considered infinity as potentialmeaning that it is the result of an endless processand were reluctant to consider infinite sets, that is sets whose number of members is not a natural number. Specific ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Musical Notation
Musical notation is any system used to visually represent music. Systems of notation generally represent the elements of a piece of music that are considered important for its performance in the context of a given musical tradition. The process of interpreting musical notation is often referred to as reading music. Distinct methods of notation have been invented throughout history by various cultures. Much information about ancient music notation is fragmentary. Even in the same time frames, different styles of music and different cultures use different music notation methods. For example, classical performers most often use sheet music using staves, time signatures, key signatures, and noteheads for writing and deciphering pieces. But even so, there are far more systems just that, for instance in professional country music, the Nashville Number System is the main method, and for string instruments such as guitar, it is quite common for tablature to be used by player ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Key Signature
In Western musical notation, a key signature is a set of sharp (), flat (), or rarely, natural () symbols placed on the staff at the beginning of a section of music. The initial key signature in a piece is placed immediately after the clef at the beginning of the first line. If the piece contains a section in a different key, the new key signature is placed at the beginning of that section. In a key signature, a sharp or flat symbol on a line or space of the staff indicates that the note represented by that line or space is to be played a semitone higher (sharp) or lower (flat) than it would otherwise be played. This applies through the rest of the piece or until another key signature appears. Each symbol applies to comparable notes in all octaves—for example, a flat on the fourth space of the treble staff (as in the diagram) indicates that all notes notated as Es are played as E-flats, including those on the bottom line of the staff. Most of this article addres ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |