|
Acceptance-rejection Method
In numerical analysis and computational statistics, rejection sampling is a basic technique used to generate observations from a probability distribution, distribution. It is also commonly called the acceptance-rejection method or "accept-reject algorithm" and is a type of exact simulation method. The method works for any distribution in \mathbb^m with a Probability density function, density. Rejection sampling is based on the observation that to sample a random variable in one dimension, one can perform a uniformly random sampling of the two-dimensional Cartesian graph, and keep the samples in the region under the graph of its density function. Note that this property can be extended to ''N''-dimension functions. Description To visualize the motivation behind rejection sampling, imagine graphing the probability density function (PDF) of a random variable onto a large rectangular board and throwing darts at it. Assume that the darts are uniformly distributed around the board. Now r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computational Statistics
Computational statistics, or statistical computing, is the study which is the intersection of statistics and computer science, and refers to the statistical methods that are enabled by using computational methods. It is the area of computational science (or scientific computing) specific to the mathematical science of statistics. This area is fast developing. The view that the broader concept of computing must be taught as part of general statistical education is gaining momentum. As in Statistics, traditional statistics the goal is to transform raw data into knowledge,Edward Wegman, Wegman, Edward J. āComputational Statistics: A New Agenda for Statistical Theory and Practice.€¯ Journal of the Washington Academy of Sciences', vol. 78, no. 4, 1988, pp. 310ā€“322. ''JSTOR'' but the focus lies on computer intensive statistical methods, such as cases with very large Sample size determination, sample size and non-homogeneous data sets. The terms 'computational statistics' and 'statis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inverse Transform Sampling
Inverse transform sampling (also known as inversion sampling, the inverse probability integral transform, the inverse transformation method, or the Smirnov transform) is a basic method for pseudo-random number sampling, i.e., for generating sample numbers at random from any probability distribution given its cumulative distribution function. Inverse transformation sampling takes uniform samples of a number u between 0 and 1, interpreted as a probability, and then returns the smallest number x\in\mathbb R such that F(x)\ge u for the cumulative distribution function F of a random variable. For example, imagine that F is the standard normal distribution with mean zero and standard deviation one. The table below shows samples taken from the uniform distribution and their representation on the standard normal distribution. We are randomly choosing a proportion of the area under the curve and returning the number in the domain such that exactly this proportion of the area occurs ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exponential Distribution
In probability theory and statistics, the exponential distribution or negative exponential distribution is the probability distribution of the distance between events in a Poisson point process, i.e., a process in which events occur continuously and independently at a constant average rate; the distance parameter could be any meaningful mono-dimensional measure of the process, such as time between production errors, or length along a roll of fabric in the weaving manufacturing process. It is a particular case of the gamma distribution. It is the continuous analogue of the geometric distribution, and it has the key property of being memoryless. In addition to being used for the analysis of Poisson point processes it is found in various other contexts. The exponential distribution is not the same as the class of exponential families of distributions. This is a large class of probability distributions that includes the exponential distribution as one of its members, but also includ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logarithmically Concave Function
In convex analysis, a non-negative function is logarithmically concave (or log-concave for short) if its domain is a convex set, and if it satisfies the inequality : f(\theta x + (1 - \theta) y) \geq f(x)^ f(y)^ for all and . If is strictly positive, this is equivalent to saying that the logarithm of the function, , is concave; that is, : \log f(\theta x + (1 - \theta) y) \geq \theta \log f(x) + (1-\theta) \log f(y) for all and . Examples of log-concave functions are the 0-1 indicator functions of convex sets (which requires the more flexible definition), and the Gaussian function. Similarly, a function is '' log-convex'' if it satisfies the reverse inequality : f(\theta x + (1 - \theta) y) \leq f(x)^ f(y)^ for all and . Properties * A log-concave function is also quasi-concave. This follows from the fact that the logarithm is monotone implying that the superlevel sets of this function are convex. * Every concave function that is nonnegative on it ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
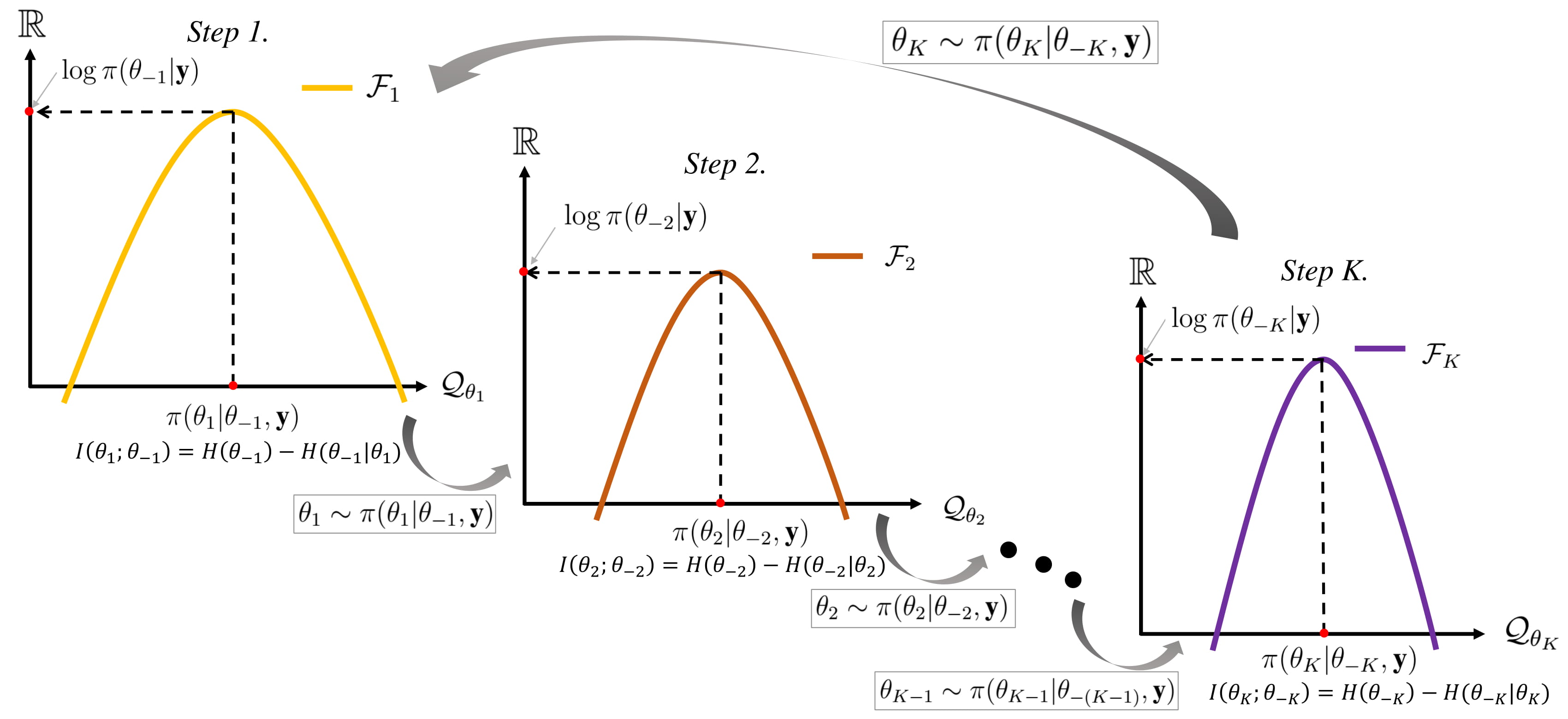
Gibbs Sampling
In statistics, Gibbs sampling or a Gibbs sampler is a Markov chain Monte Carlo (MCMC) algorithm for sampling from a specified multivariate distribution, multivariate probability distribution when direct sampling from the joint distribution is difficult, but sampling from the Conditional probability distribution, conditional distribution is more practical. This sequence can be used to approximate the joint distribution (e.g., to generate a histogram of the distribution); to approximate the marginal distribution of one of the variables, or some subset of the variables (for example, the unknown parameters or latent variables); or to compute an integral (such as the expected value of one of the variables). Typically, some of the variables correspond to observations whose values are known, and hence do not need to be sampled. Gibbs sampling is commonly used as a means of statistical inference, especially Bayesian inference. It is a randomized algorithm (i.e. an algorithm that makes ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Metropolis Sampling
A metropolis () is a large city or conurbation which is a significant economic, political, and cultural area for a country or region, and an important hub for regional or international connections, commerce, and communications. A big city belonging to a larger urban agglomeration, but which is not the core of that agglomeration, is not generally considered a metropolis but a part of it. The plural of the word is ''metropolises'', although the Latin plural is , from the Greek (). For urban areas outside metropolitan areas that generate a similar attraction on a smaller scale for their region, the concept of the regiopolis ("regio" for short) was introduced by urban and regional planning researchers in Germany in 2006. Etymology () is a Greek word, (plural: ) coming from , meaning "mother" and , meaning "city" or "town", which is how the Greek colonies of antiquity referred to their original cities, with whom they retained cultic and political-cultural connections. The wo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |