|
83 (number)
83 (eighty-three) is the natural number following 82 and preceding 84. In mathematics 83 is: * the sum of three consecutive primes (23 + 29 + 31). * the sum of five consecutive primes (11 + 13 + 17 + 19 + 23). * the 23rd prime number, following 79 (of which it is also a cousin prime) and preceding 89. * a Sophie Germain prime. * a safe prime. * a Chen prime. * an Eisenstein prime with no imaginary part and real part of the form 3''n'' − 1. * a highly cototient number. * the number of primes that are right-truncatable. * a super-prime, because 23 is prime. In other fields * The eighth letter of the alphabet is H and the third letter is C, thus 83 stands for "Heil Christ," a greeting used by organizations that consider themselves also to be Christian. * An emoticon An emoticon (, , rarely , ), short for emotion icon, is a pictorial representation of a facial expression using Character (symbol), characters—usually punctuation marks, numbers and Alphabet, l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prime Number
A prime number (or a prime) is a natural number greater than 1 that is not a Product (mathematics), product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways of writing it as a product, or , involve 5 itself. However, 4 is composite because it is a product (2 × 2) in which both numbers are smaller than 4. Primes are central in number theory because of the fundamental theorem of arithmetic: every natural number greater than 1 is either a prime itself or can be factorization, factorized as a product of primes that is unique up to their order. The property of being prime is called primality. A simple but slow primality test, method of checking the primality of a given number , called trial division, tests whether is a multiple of any integer between 2 and . Faster algorithms include the Miller–Rabin primality test, which is fast but has a small chance of error ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Natural Number
In mathematics, the natural numbers are the numbers 0, 1, 2, 3, and so on, possibly excluding 0. Some start counting with 0, defining the natural numbers as the non-negative integers , while others start with 1, defining them as the positive integers Some authors acknowledge both definitions whenever convenient. Sometimes, the whole numbers are the natural numbers as well as zero. In other cases, the ''whole numbers'' refer to all of the integers, including negative integers. The counting numbers are another term for the natural numbers, particularly in primary education, and are ambiguous as well although typically start at 1. The natural numbers are used for counting things, like "there are ''six'' coins on the table", in which case they are called ''cardinal numbers''. They are also used to put things in order, like "this is the ''third'' largest city in the country", which are called ''ordinal numbers''. Natural numbers are also used as labels, like Number (sports), jersey ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
82 (number)
82 (eighty-two) is the natural number following 81 and preceding 83. In mathematics 82 is: * the twenty-seventh semiprime and the thirteenth of the form (2.q). * with an aliquot sum of 44, within an aliquot sequence of four composite numbers (82, 44, 40, 50, 43, 1,0) to the Prime in the 43-aliquot tree. * a companion Pell number. * a happy number. * palindromic A palindrome ( /ˈpæl.ɪn.droʊm/) is a word, number, phrase, or other sequence of symbols that reads the same backwards as forwards, such as ''madam'' or '' racecar'', the date " 02/02/2020" and the sentence: "A man, a plan, a canal – Pana ... in bases 3 (100013), 9 (1019) and 40 (2240). In science *The sixth magic number. References Integers {{Num-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
84 (number)
84 (eighty-four) is the natural number following 83 (number), 83 and preceding 85 (number), 85. It is seven dozen, dozens. In mathematics 84 is a semiperfect number, being thrice a perfect number, and the sum of the sixth pair of twin primes (41 + 43). It is the number of four-digit perfect powers in decimal. It is the third (or the 2) dodecahedral number, and the sum of the first seven triangular numbers (1, 3, 6, 10, 15, 21, 28), which makes it the seventh tetrahedral number. The number of divisors of 84 is 12. As no smaller number has more than 12 divisors, 84 is a largely composite number. The twenty-second unique prime in Base ten, decimal, with notably different Numerical digit, digits than its preceding (and known following) terms in the same sequence, contains a total of 84 digits. A hepteract is a seven-dimensional hypercube with 84 penteract 5-faces. 84 is the limit superior of the largest finite subgroup of the mapping class group of a genus g surface divided by ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
79 (number)
79 (seventy-nine) is the natural number following 78 (number), 78 and preceding 80 (number), 80. In mathematics 79 is: * An even and odd numbers, odd number. * The smallest number that can not be represented as a sum of fewer than 19 fourth powers. * The 22nd prime number (between and ) * An isolated prime without a twin prime, as 77 and 81 are composite. * The smallest prime number ''p'' for which the real quadratic field Q[] has Ideal class group, class number greater than 1 (namely 3). * A cousin prime with 83. * An emirp in base 10, because the reverse of 79, 97 (number), 97, is also a prime. * A Fortunate prime. * A circular prime. * A prime number that is also a Gaussian prime (since it is of the form ). * A happy prime. * A Higgs prime. * A lucky prime. * A permutable prime, with 97 (number), ninety-seven. * A Pillai prime, because 23Factorial, ! + 1 is divisible by 79, but 79 is not one more than a Multiple (mathematics), multiple of 23 (number), 23. * A regular prime. * A ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cousin Prime
In number theory, cousin primes are prime numbers that differ by four. Compare this with twin primes, pairs of prime numbers that differ by two, and sexy primes, pairs of prime numbers that differ by six. The cousin primes (sequences and in OEIS) below 1000 are: :(3, 7), (7, 11), (13, 17), (19, 23), (37, 41), (43, 47), (67, 71), (79, 83), (97, 101), (103, 107), (109, 113), (127, 131), (163, 167), (193, 197), (223, 227), (229, 233), (277, 281), (307, 311), (313, 317), (349, 353), (379, 383), (397, 401), (439, 443), (457, 461), (463,467), (487, 491), (499, 503), (613, 617), (643, 647), (673, 677), (739, 743), (757, 761), (769, 773), (823, 827), (853, 857), (859, 863), (877, 881), (883, 887), (907, 911), (937, 941), (967, 971) Properties The only prime belonging to two pairs of cousin primes is 7. One of the numbers will always be divisible by 3, so is the only case where all three are primes. An example of a large proven cousin prime pair is for :p = 4111286921397 \times ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
89 (number)
89 (eighty-nine) is the natural number following 88 and preceding 90. In mathematics 89 is: * the 24th prime number, following 83 and preceding 97. * a Chen prime. * a Pythagorean prime. * the smallest Sophie Germain prime to start a Cunningham chain of the first kind of six terms, . * an Eisenstein prime with no imaginary part and real part of the form . * The 11th Fibonacci number and thus a Fibonacci prime as well. The first few digits of its reciprocal coincide with the Fibonacci sequence due to the identity ::\frac=\sum_^\infty=0.011235955\dots\ . * a Markov number, appearing in solutions to the Markov Diophantine equation with other odd-indexed Fibonacci numbers. ''M''89 is the 10th Mersenne prime. Although 89 is not a Lychrel number in base 10, it is unusual that it takes 24 iterations of the reverse and add process to reach a palindrome. Among the known non-Lychrel numbers in the first 10000 integers, no other number requires that many or more iterations. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sophie Germain Prime
In number theory, a prime number ''p'' is a if 2''p'' + 1 is also prime. The number 2''p'' + 1 associated with a Sophie Germain prime is called a . For example, 11 is a Sophie Germain prime and 2 × 11 + 1 = 23 is its associated safe prime. Sophie Germain primes and safe primes have applications in public key cryptography and primality testing. It has been conjectured that there are infinitely many Sophie Germain primes, but this remains unproven. Sophie Germain primes are named after French mathematician Sophie Germain, who used them in her investigations of Fermat's Last Theorem. One attempt by Germain to prove Fermat’s Last Theorem was to let ''p'' be a prime number of the form 8''k'' + 7 and to let ''n'' = ''p'' – 1. In this case, x^n + y^n = z^n is unsolvable. Germain’s proof, however, remained unfinished. Through her attempts to solve Fermat's Last Theorem, Germain developed a result now known as Germain's Theore ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chen Prime
In mathematics, a prime number ''p'' is called a Chen prime if ''p'' + 2 is either a prime or a product of two primes (also called a semiprime). The even number 2''p'' + 2 therefore satisfies Chen's theorem. The Chen primes are named after Chen Jingrun, who proved in 1966 that there are infinitely many such primes. This result would also follow from the truth of the twin prime conjecture as the lower member of a pair of twin primes is by definition a Chen prime. The first few Chen primes are : 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 47, 53, 59, 67, 71, 83, 89, 101, … . The first few Chen primes that are not the lower member of a pair of twin primes are :2, 7, 13, 19, 23, 31, 37, 47, 53, 67, 83, 89, 109, 113, 127, ... . The first few non-Chen primes are :43, 61, 73, 79, 97, 103, 151, 163, 173, 193, 223, 229, 241, … . All of the supersingular primes are Chen primes. Rudolf Ondrejka discovered the following 3 × 3 m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
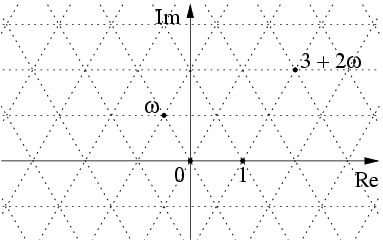
Eisenstein Prime
In mathematics, the Eisenstein integers (named after Gotthold Eisenstein), occasionally also known as Eulerian integers (after Leonhard Euler), are the complex numbers of the form : z = a + b\omega , where and are integers and : \omega = \frac = e^ is a primitive (hence non-real) cube root of unity. The Eisenstein integers form a triangular lattice in the complex plane, in contrast with the Gaussian integers, which form a square lattice in the complex plane. The Eisenstein integers are a countably infinite set. Properties The Eisenstein integers form a commutative ring of algebraic integers in the algebraic number field – the third cyclotomic field. To see that the Eisenstein integers are algebraic integers note that each is a root of the monic polynomial : z^2 - (2a - b)\;\!z + \left(a^2 - ab + b^2\right)~. In particular, satisfies the equation : \omega^2 + \omega + 1 = 0~. The product of two Eisenstein integers and is given explicitly by : (a + b\;\!\omega) \;\ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Highly Cototient Number
In number theory, a branch of mathematics, a highly cototient number is a positive integer k which is above 1 and has more solutions to the equation :x - \phi(x) = k than any other integer below k and above 1. Here, \phi is Euler's totient function. There are infinitely many solutions to the equation for :k = 1 so this value is excluded in the definition. The first few highly cototient numbers are:. : 2, 4, 8, 23, 35, 47, 59, 63, 83, 89, 113, 119, 167, 209, 269, 299, 329, 389, 419, 509, 629, 659, 779, 839, 1049, 1169, 1259, 1469, 1649, 1679, 1889, ... Many of the highly cototient numbers are odd. The concept is somewhat analogous to that of highly composite numbers. Just as there are infinitely many highly composite numbers, there are also infinitely many highly cototient numbers. Computations become harder, since integer factorization becomes harder as the numbers get larger. Example The cototient of x is defined as x - \phi(x), i.e. the number of positive ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |