Zometool on:
[Wikipedia]
[Google]
[Amazon]
Zometool is a  The Zometool plastic
The Zometool plastic
 The color of a Zometool strut is associated with its cross section and also with the shape of the hole of the connector node in which it fits. Each blue strut has a rectangular cross section, each yellow strut has a triangular cross section, and each red strut has a
The color of a Zometool strut is associated with its cross section and also with the shape of the hole of the connector node in which it fits. Each blue strut has a rectangular cross section, each yellow strut has a triangular cross section, and each red strut has a
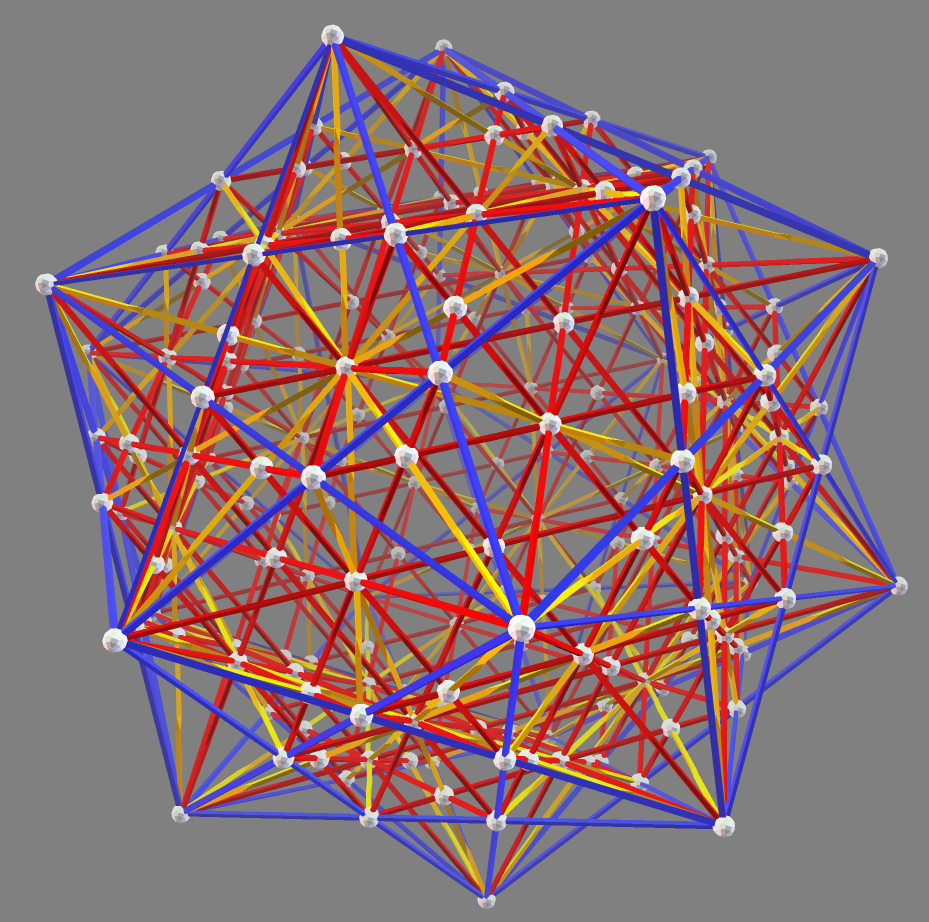 The zome system is especially useful for modeling 1-dimensional skeletons of highly symmetric objects in 3- and 4-dimensional Euclidean space. The most prominent among these are the five
The zome system is especially useful for modeling 1-dimensional skeletons of highly symmetric objects in 3- and 4-dimensional Euclidean space. The most prominent among these are the five
''Zome Primer.''
Zomeworks Corporation, 1970. * David Booth
''The New Zome Primer''
in ''Fivefold Symmetry,'' István Hargittai (editor). World Scientific Publishing Company, 1992. * George Hart
''Four-Dimensional Polytope Projection Barn Raisings.''
Proceedings, Sixth International Conference of the Society of Art, Math, and Architecture, Texas A&M University. May 2007. * George Hart and Henri Picciotto. ''Zome Geometry: Hands-on Learning with Zome Models.'' Key Curriculum Press, 2001. . * Paul R. Hildebrandt & Marc G. Pelletier (1985)
"Geometric Modeling Kit and Method of Making Same"
United States Patent No. 4,701,131. * Paul Hildebrandt. Zome-inspired Sculpture. ''Proceedings, Bridges London: Connections between Mathematics, Art, and Music'', Reza Sarhangi and John Sharp (editors). (2006) 335–342. * David A. Richter. Two results concerning the Zome model of the 600-cell. ''Proceedings, Renaissance Banff: Mathematical Connections between Mathematics, Art, and Music'', Robert Moody and Reza Sarhangi (editors). (2005) 419–426. * David A. Richter and Scott Vorthmann. Green Quaternions, Tenacious Symmetry, and Octahedral Zome. ''Proceedings, Bridges London: Connections between Mathematics, Art, and Music'', Reza Sarhangi and John Sharp (editors). (2006) 429–436. * Steven F. Rogers & Paul R. Hildebrandt (2002
"Connections for Geometric Modeling Kit"
United States Patent No. 6,840,699 B2.
by
Henri Picciotto
Zometool
- Manufacturer's site.
Japan Zome Club (in Japanese)
* {{MathWorld, urlname=Zome, title=Zome Software
vZome
Construction toys Educational toys Mathematical tools
construction set toy
A construction set is a standardized piece assortment allowing for the construction of various different models. Construction sets are most often marketed as toys. Popular construction toy brands include Lincoln Logs and ''LEGO''.
Toys
...
that had been created by a collaboration of Steve Baer
Steve Baer (October 13, 1938 – May 17, 2024) was an American inventor and pioneer of passive solar technology. Baer pioneered and helped popularize the use of zomes. He took a number of solar power patents, wrote a number of books and publiciz ...
(the creator of Zome architecture), artist Clark Richert
Clark Richert (May 3, 1941 – December 24, 2021) was an American contemporary artist largely known for his colorful geometric paintings, but whose practice included animation, video, intervention, happenings, and publishing. He also developed Dr ...
, Paul Hildebrandt (the present CEO of Zometool), and co-inventor Marc Pelletier. It is manufactured by Zometool, Inc. According to the company, Zometool was primarily designed for kids. Zometool has also been used in other fields including mathematics and physics. For example, aperiodic tiling
An aperiodic tiling is a non-periodic Tessellation, tiling with the additional property that it does not contain arbitrarily large periodic regions or patches. A set of tile-types (or prototiles) is aperiodic set of prototiles, aperiodic if copie ...
s such as Penrose tiling
A Penrose tiling is an example of an aperiodic tiling. Here, a ''tiling'' is a covering of two-dimensional space, the plane by non-overlapping polygons or other shapes, and a tiling is ''aperiodic'' if it does not contain arbitrarily large Perio ...
s can be modeled using Zometool. The learning tool was designed by inventor-designer Steve Baer, his wife Holly and others.
 The Zometool plastic
The Zometool plastic construction set toy
A construction set is a standardized piece assortment allowing for the construction of various different models. Construction sets are most often marketed as toys. Popular construction toy brands include Lincoln Logs and ''LEGO''.
Toys
...
is produced by a privately owned company of the same name, based outside of Longmont, Colorado
Longmont is a home rule municipality located in Boulder and Weld counties, Colorado, United States. Its population was 98,885 . Longmont is located northeast of the county seat of Boulder. It is named after Longs Peak, a prominent mountain th ...
, and which evolved out of Baer's company ZomeWorks. Its elements consist of small connector nodes and struts of various colors. The overall shape of a connector node is that of a non-uniform small rhombicosidodecahedron
In geometry, the rhombicosidodecahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed of two or more types of regular polygon faces.
It has a total of 62 faces: 20 regular triangular faces, 30 square f ...
with each face replaced by a small hole. The ends of the struts are designed to fit in the holes of the connector nodes, allowing for syntheses of a variety of structures. The idea of shape-coding the three types of struts was developed by Marc Pelletier and Paul Hildebrandt. To create the "balls," or nodes, Pelletier and Hildebrandt invented a system of 62 hydraulic pins that came together to form a mold. The first connector node emerged from their mold on April 1, 1992.
In the years since 1992, Zometool has extended its product line, though the basic design of the connector node has not changed so all parts to date are compatible with each-other. From 1992 until 2000, Zometool produced kits with connector nodes and blue, yellow, and red struts. In 2000, Zometool introduced green struts, prompted by French architect Fabien Vienne
Fabien Vienne (18 February 1925 - 31 March 2016) was a French architect, urban planner, and designer. Born in Paris, Vienne initially pursued a technical education and graduated from the École des Arts-Appliqués. Throughout his career, he ...
, which can be used to construct the regular tetrahedron and octahedron. In 2003, Zometool changed the style of the struts slightly. The struts "with clicks" have a different surface texture and they also have longer nibs which allow for a more robust connection between connector node and strut.
Characteristics
 The color of a Zometool strut is associated with its cross section and also with the shape of the hole of the connector node in which it fits. Each blue strut has a rectangular cross section, each yellow strut has a triangular cross section, and each red strut has a
The color of a Zometool strut is associated with its cross section and also with the shape of the hole of the connector node in which it fits. Each blue strut has a rectangular cross section, each yellow strut has a triangular cross section, and each red strut has a pentagon
In geometry, a pentagon () is any five-sided polygon or 5-gon. The sum of the internal angles in a simple polygon, simple pentagon is 540°.
A pentagon may be simple or list of self-intersecting polygons, self-intersecting. A self-intersecting ...
al cross section. The cross section of a green strut is a rhombus of √2 aspect ratio, but as the connector nodes do not include holes at the required positions, the green struts instead fit into any of the 12 pentagonal holes with 5 possible orientations per hole, 60 possible orientations in all; using them is not as straightforward as the other struts.
At their midpoints, each of the yellow and red struts has a twist where the cross-sectional shape reverses. This design feature forces the connector nodes on the ends of the strut to have the same orientation. Similarly, the cross section of the blue strut is a non-square rectangle, again ensuring that the two nodes on the ends have the same orientation. Instead of a twist, the green struts have two bends which allow them to fit into the pentagonal holes of the connector node which are at a slight offset from the strut's axis.
Among other places, the word zome comes from the term zone. The zome system allows no more than 61 zones. The cross-sectional shapes correspond to colors, and in turn these correspond to zone colors. Hence the zome system has 15 blue zones, 10 yellow zones, 6 red zones, and 30 green zones. Two shapes are associated with blue. The blue struts with a rectangular cross section are designed to lie in the same zones as the blue struts, but they are half the length of a blue strut; hence these struts are often called "half-blue" (and were originally made in a light blue color). The blue-green struts with a rhombic cross section lie in the same zones as the green struts, but they are designed so that the ratio of a rhombic blue-green strut to a blue strut is 1:1 (as opposed to the green strut's √2:1). Due to this length ratio, the blue-green struts that have a rhombic cross section do not mathematically belong to the zome system.
Mathematics of Zometools
The strut lengths follow a mathematical pattern: For any color, there exists lengths such that they increase by a constant factor of approximately 1.618, a number that is yield of what is called the “golden ratio
In mathematics, two quantities are in the golden ratio if their ratio is the same as the ratio of their summation, sum to the larger of the two quantities. Expressed algebraically, for quantities and with , is in a golden ratio to if
\fr ...
" which is represented by Greek letter phi
Phi ( ; uppercase Φ, lowercase φ or ϕ; ''pheî'' ; Modern Greek: ''fi'' ) is the twenty-first letter of the Greek alphabet.
In Archaic and Classical Greek (c. 9th to 4th century BC), it represented an aspirated voiceless bilabial plos ...
( or ).The Mathematics of Zome
Tom Davis
http://www.geometer.org/mathcircles
July 4, 2007 The golden ratio is a ratio such that the sum of two quantities is equal to the ratio of the same quantities, based on the largest value of the two numbers.
Thus,
An application of the golden ratio for the zome system is that for each color,
there exists a length such that a long strut length equals the length of a medium strut connected to a short strut.
In other words, the length of the long strut equals the sum of the medium strut length and the a short strut length.
Definition
A zome is defined in terms of the vector space , equipped with the standard inner product, also known as 3-dimensional Euclidean space. Let denote thegolden ratio
In mathematics, two quantities are in the golden ratio if their ratio is the same as the ratio of their summation, sum to the larger of the two quantities. Expressed algebraically, for quantities and with , is in a golden ratio to if
\fr ...
and let denote the symmetry group
In group theory, the symmetry group of a geometric object is the group of all transformations under which the object is invariant, endowed with the group operation of composition. Such a transformation is an invertible mapping of the amb ...
of the configuration of vectors , , and . The group , an example of a Coxeter group
In mathematics, a Coxeter group, named after H. S. M. Coxeter, is an abstract group that admits a formal description in terms of reflections (or kaleidoscopic mirrors). Indeed, the finite Coxeter groups are precisely the finite Euclidean ref ...
, is known as the icosahedral group because it is the symmetry group of a regular icosahedron
In geometry, an icosahedron ( or ) is a polyhedron with 20 faces. The name comes . The plural can be either "icosahedra" () or "icosahedrons".
There are infinitely many non- similar shapes of icosahedra, some of them being more symmetrical tha ...
having these vectors as its vertices. The subgroup of consisting of the elements with determinant 1 (i.e. the rotations) is isomorphic to .
Define the "standard blue vectors" as the -orbit of the vector . Define the "standard yellow vectors" as the -orbit of the vector . Define the "standard red vectors" as the -orbit of the vector . A "strut" of the zome system is any vector which can be obtained from the standard vectors described above by scaling by any power , where is an integer. A "node" of the zome system is any element of the subgroup of generated by the struts. Finally, the "zome system" is the set of all pairs , where is a set of nodes and is a set of pairs such that and are in and the difference is a strut.
There are then 30, 20, and 12 standard vectors having the colors blue, yellow, and red, respectively. Correspondingly, the stabilizer subgroup of a blue, yellow, or red strut is isomorphic to the cyclic group of order 2, 3, or 5, respectively. Hence, one may also describe the blue, yellow, and red struts as "rectangular", "triangular", and "pentagonal", respectively.
The zome system may be extended by adjoining green vectors. The "standard green vectors" comprise the -orbit of the vector and a "green strut" as any vector which can be obtained by scaling a standard green vector by any integral power . As above, one may check that there are =60 standard green vectors. One may then enhance the zome system by including these green struts. Doing this does not affect the set of nodes.
The abstract zome system defined above is significant because of the following fact: Every connected zome model has a faithful image in the zome system. The converse of this fact is only partially true, but this is due only to the laws of physics. For example, the radius of a zometool node is positive (as opposed to a node being a single point mathematically), so one cannot make a zometool model where two nodes are separated by an arbitrarily small, prescribed distance. Similarly, only a finite number of lengths of struts will ever be manufactured, and a green strut cannot be placed directly adjacent to a red strut or another green strut with which it shares the same hole (even though they are mathematically distinct).
As a modeling system
 The zome system is especially useful for modeling 1-dimensional skeletons of highly symmetric objects in 3- and 4-dimensional Euclidean space. The most prominent among these are the five
The zome system is especially useful for modeling 1-dimensional skeletons of highly symmetric objects in 3- and 4-dimensional Euclidean space. The most prominent among these are the five Platonic Solids
In geometry, a Platonic solid is a convex, regular polyhedron in three-dimensional Euclidean space. Being a regular polyhedron means that the faces are congruent (identical in shape and size) regular polygons (all angles congruent and all edge ...
, and the 4-dimensional polytopes related to the 120-cell
In geometry, the 120-cell is the convex regular 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol . It is also called a C120, dodecaplex (short for "dodecahedral complex"), hyperdodecahedron, polydodecahedron, hec ...
and the 600-cell
In geometry, the 600-cell is the convex regular 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol .
It is also known as the C600, hexacosichoron and hexacosihedroid.
It is also called a tetraplex (abbreviated from ...
. However, many other mathematical objects may be modeled using the zome system, including:
* Three of the four Kepler-Poinsot polyhedra
* Regular polyhedral compound
In geometry, a polyhedral compound is a figure that is composed of several polyhedra sharing a common Centroid, centre. They are the three-dimensional analogs of star polygon#Regular compounds, polygonal compounds such as the hexagram.
The oute ...
s
* Regular 4-dimensional polytopes and some compounds
* Many stellations of the rhombic triacontahedron
The rhombic triacontahedron, sometimes simply called the triacontahedron as it is the most common thirty-faced polyhedron, is a convex polyhedron with 30 rhombus, rhombic face (geometry), faces. It has 60 edge (geometry), edges and 32 vertex ...
* Many stellations of the regular icosahedron
In geometry, an icosahedron ( or ) is a polyhedron with 20 faces. The name comes . The plural can be either "icosahedra" () or "icosahedrons".
There are infinitely many non- similar shapes of icosahedra, some of them being more symmetrical tha ...
* Zonohedra
In geometry, a zonohedron is a convex polyhedron that is point symmetry, centrally symmetric, every face of which is a polygon that is centrally symmetric (a zonogon). Any zonohedron may equivalently be described as the Minkowski addition, Minkows ...
, especially the rhombic enneacontahedron
In geometry, a rhombic enneacontahedron (plural: rhombic enneacontahedra) is a polyhedron composed of 90 rhombic faces; with three, five, or six rhombi meeting at each vertex. It has 60 broad rhombi and 30 slim. The rhombic enneacontahedron is a ...
and rhombic triacontahedron
The rhombic triacontahedron, sometimes simply called the triacontahedron as it is the most common thirty-faced polyhedron, is a convex polyhedron with 30 rhombus, rhombic face (geometry), faces. It has 60 edge (geometry), edges and 32 vertex ...
* Hypercube
In geometry, a hypercube is an ''n''-dimensional analogue of a square ( ) and a cube ( ); the special case for is known as a ''tesseract''. It is a closed, compact, convex figure whose 1- skeleton consists of groups of opposite parallel l ...
s in dimensions 61 or fewer
* Most uniform polyhedra
In geometry, a uniform polyhedron has regular polygons as faces and is vertex-transitive—there is an isometry mapping any vertex onto any other. It follows that all vertices are congruent. Uniform polyhedra may be regular (if also fac ...
(a major exception being those formed using the snub
A snub, cut, or slight is a refusal to recognise an acquaintance by ignoring them, avoiding them or pretending not to know them. For example, a failure to greet someone may be considered a snub.
In awards and lists
For awards, the term "snub ...
operation)
* Many uniform 4-polytope
In geometry, a uniform 4-polytope (or uniform polychoron) is a 4-dimensional polytope which is vertex-transitive and whose cells are uniform polyhedron, uniform polyhedra, and faces are regular polygons.
There are 47 non-Prism (geometry), prism ...
s
* Thorold Gosset's exceptional semiregular polytopes in 6, 7, and 8 dimensions
* Some Johnson solid
In geometry, a Johnson solid, sometimes also known as a Johnson–Zalgaller solid, is a convex polyhedron whose faces are regular polygons. They are sometimes defined to exclude the uniform polyhedrons. There are ninety-two Solid geometry, s ...
s
* Desargues configuration
In geometry, the Desargues configuration is a Configuration (geometry), configuration of ten points and ten lines, with three points per line and three lines per point. It is named after Girard Desargues.
The Desargues configuration can be const ...
* Two of the Catalan solid
The Catalan solids are the dual polyhedron, dual polyhedra of Archimedean solids. The Archimedean solids are thirteen highly-symmetric polyhedra with regular faces and symmetric vertices. The faces of the Catalan solids correspond by duality to ...
s
* Classical and exceptional root system
In mathematics, a root system is a configuration of vector space, vectors in a Euclidean space satisfying certain geometrical properties. The concept is fundamental in the theory of Lie groups and Lie algebras, especially the classification and ...
s
* Triality
In mathematics, triality is a relationship among three vector spaces, analogous to the duality relation between dual vector spaces. Most commonly, it describes those special features of the Dynkin diagram D4 and the associated Lie group Spin(8 ...
(from Lie theory)
The uses of zome are not restricted to pure mathematics. Other uses include the study of engineering problems, especially steel-truss structures, the study of some molecular
A molecule is a group of two or more atoms that are held together by attractive forces known as chemical bonds; depending on context, the term may or may not include ions that satisfy this criterion. In quantum physics, organic chemistry, ...
, nanotube
A nanotube is a nanoscale cylindrical structure with a hollow core, typically composed of carbon atoms, though other materials can also form nanotubes. Carbon nanotubes (CNTs) are the most well-known and widely studied type, consisting of rolled- ...
, and viral
The word ''Viral'' means "relating to viruses" (small infectious agents).
It may also refer to:
Viral behavior, or virality
Memetic behavior likened that of a virus, for example:
* Viral marketing, the use of existing social networks to spre ...
structures, and to make soap film surfaces.
References
Further reading
* Steve Baer''Zome Primer.''
Zomeworks Corporation, 1970. * David Booth
''The New Zome Primer''
in ''Fivefold Symmetry,'' István Hargittai (editor). World Scientific Publishing Company, 1992. * George Hart
''Four-Dimensional Polytope Projection Barn Raisings.''
Proceedings, Sixth International Conference of the Society of Art, Math, and Architecture, Texas A&M University. May 2007. * George Hart and Henri Picciotto. ''Zome Geometry: Hands-on Learning with Zome Models.'' Key Curriculum Press, 2001. . * Paul R. Hildebrandt & Marc G. Pelletier (1985)
"Geometric Modeling Kit and Method of Making Same"
United States Patent No. 4,701,131. * Paul Hildebrandt. Zome-inspired Sculpture. ''Proceedings, Bridges London: Connections between Mathematics, Art, and Music'', Reza Sarhangi and John Sharp (editors). (2006) 335–342. * David A. Richter. Two results concerning the Zome model of the 600-cell. ''Proceedings, Renaissance Banff: Mathematical Connections between Mathematics, Art, and Music'', Robert Moody and Reza Sarhangi (editors). (2005) 419–426. * David A. Richter and Scott Vorthmann. Green Quaternions, Tenacious Symmetry, and Octahedral Zome. ''Proceedings, Bridges London: Connections between Mathematics, Art, and Music'', Reza Sarhangi and John Sharp (editors). (2006) 429–436. * Steven F. Rogers & Paul R. Hildebrandt (2002
"Connections for Geometric Modeling Kit"
United States Patent No. 6,840,699 B2.
External links
by
George W. Hart
George William Hart (born 1955) is an American sculptor and geometer. Before retiring, he was an associate professor of Electrical Engineering at Columbia University in New York City and then an interdepartmental research professor at Stony Bro ...
anHenri Picciotto
Zometool
- Manufacturer's site.
Japan Zome Club (in Japanese)
* {{MathWorld, urlname=Zome, title=Zome Software
vZome
Construction toys Educational toys Mathematical tools