Zero-inflated Model

In statistics, a zero-inflated model is a statistical model based on a zero-inflated probability distribution, i.e. a distribution that allows for frequent zero-valued observations.

Introduction to zero-inflated models

Zero-inflated models are commonly used in the analysis of count data, such as the number of visits a patient makes to the emergency room in one year, or the number of fish caught in one day in one lake.
Count data can take values of 0, 1, 2, … (non-negative integer values).
Other examples of count data are the number of hits recorded by a Geiger counter in one minute, patient days in the hospital, goals scored in a soccer game,
and the number of episodes of hypoglycemia per year for a patient with diabetes.

For statistical analysis, the distribution of the counts is often represented using a Poisson distribution or a negative binomial distribution. Hilbe notes that "Poisson regression is traditionally conceived of as the basic count model upon which a variety of other count models are based." In a Poisson model, "… the random variable $y$ is the count response and parameter $\lambda$ (lambda) is the mean. Often, $\lambda$ is also called the rate or intensity parameter… In statistical literature, $\lambda$ is also expressed as $\mu$ (mu) when referring to Poisson and traditional negative binomial models."

In some data, the number of zeros is greater than would be expected using a Poisson distribution or a negative binomial distribution. Data with such an excess of zero counts are described as Zero-inflated.

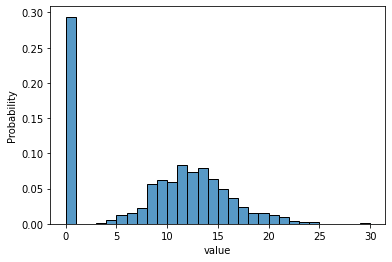
Example histograms of zero-inflated Poisson distributions with mean $\mu$ of 5 or 10 and proportion of zero inflation $\pi$ of 0.2 or 0.5 are shown below, based on the R program ZeroInflPoiDistPlots.R from Bilder and Laughlin.

Examples of zero-inflated count data

* Fish counts "… suppose we recorded the number of fish caught on various lakes in 4-hour fishing trips to Minnesota. Some lakes in Minnesota are too shallow for fish to survive the winter, so fishing in those lakes will yield no catch. On the other hand, even on a lake where fish are plentiful, we may or may not catch any fish due to conditions or our own competence. Thus, the number of fish caught will be zero if the lake does not support fish, and will be zero, one or more if it does."
* Number of wisdom teeth extracted. The number of wisdom teeth that a person has had extracted can range from 0 to 4. Some individuals, about one-third of the population, do not have any wisdom teeth. For these individuals, the number of wisdom teeth extracted will always be zero. For other individuals, the number extracted will be between 0 and 4, where a 0 indicates that the subject has not yet, and may never, have any of their 4 wisdom teeth extracted.
* Publications by PhD candidates.
Long examined the number of publications by 915 doctoral candidates in biochemistry in the last three years of their PhD studies. The proportion of candidates with zero publications exceeded the number predicted by a Poisson model. "Long argued that the PhD candidates might fall into two distinct groups: "publishers" (perhaps striving for an academic career) and "non-publishers" (seeking other career paths). One reasonable form of explanation is that the observed zero counts reflect a mixture of the two latent classes – those who simply have not yet published and those who will likely never publish."

Zero-inflated data as a mixture of two distributions

As the examples above show, zero-inflated data can arise as a mixture of two distributions. The first distribution generates zeros. The second distribution, which may be a Poisson distribution, a negative binomial distribution or other count distribution, generates counts, some of which may be zeros.

In the statistical literature, different authors may use different names to distinguish zeros from the two distributions. Some authors describe zeros generated by the first (binary) distribution as "structural" and zeros generated by the second (count) distribution as "random". Other authors use the terminology "immune" and "susceptible" for the binary and count zeros, respectively.

Zero-inflated Poisson

One well-known zero-inflated model is Diane Lambert's zero-inflated Poisson model, which concerns a random event containing excess zero-count data in unit time. For example, the number of insurance claims within a population for a certain type of risk would be zero-inflated by those people who have not taken out insurance against the risk and thus are unable to claim. The zero-inflated Poisson (ZIP) model mixes two zero generating processes. The first process generates zeros. The second process is governed by a Poisson distribution that generates counts, some of which may be zero. The mixture distribution is described as follows:

:$\Pr (Y = 0) = \pi + (1 - \pi) e^$
:$\Pr (Y = y_i) = (1 - \pi) \frac ,\qquad y_i = 1,2,3,...$

where the outcome variable $y_i$ has any non-negative integer value, $\lambda$ is the expected Poisson count for the $i$th individual; $\pi$ is the probability of extra zeros.

The mean is $(1-\pi) \lambda$ and the variance is $\lambda (1-\pi) (1+\pi \lambda)$.

Estimators of ZIP parameters

The method of moments estimators are given by

: $\hat_ = \frac - 1,$

: $\hat_ = \frac,$

where $m$ is the sample mean and $s^2$ is the sample variance.

The maximum likelihood estimator can be found by solving the following equation

: $m(1- e^) = \hat_ \left( 1 - \frac \right).$

where $\frac$ is the observed proportion of zeros.

A closed form solution of this equation is given by

:$\hat_ = W_(-s e^)+s$

with $W_0$ being the main branch of Lambert's W-function and

:$s = \frac$.

Alternatively, the equation can be solved by iteration.

The maximum likelihood estimator for $\pi$ is given by

: $\hat_ = 1 - \frac.$

Related models

In 1994, Greene considered the zero-inflated negative binomial (ZINB) model. Daniel B. Hall adapted Lambert's methodology to an upper-bounded count situation, thereby obtaining a zero-inflated binomial (ZIB) model.

Discrete pseudo compound Poisson model

If the count data $Y$ is such that the probability of zero is larger than the probability of nonzero, namely

:$\Pr (Y = 0) > 0.5$

then the discrete data $Y$ obey discrete pseudo compound Poisson distribution.

In fact, let $G(z) = \sum\limits_^\infty P(Y = n)z^n$ be the probability generating function of $y_i$. If $p_0=\Pr (Y = 0) > 0.5$, then $, G(z), \geqslant p_0 - \sum\limits_^\infty p_i = 2p_0-1 > 0$. Then from the Wiener–Lévy theorem, $G(z)$ has the probability generating function of the discrete pseudo compound Poisson distribution.

We say that the discrete random variable $Y$ satisfying probability generating function characterization

:$G_Y(z) = \sum\limits_^\infty P(Y = n)z^n = \exp\left(\sum_^\infty \alpha_k \lambda (z^k - 1)\right), \quad (, z, \le 1)$

has a discrete pseudo compound Poisson distribution with parameters

: $(\lambda_1, \lambda_2, \ldots ) = (\alpha_1 \lambda,\alpha_2 \lambda, \ldots ) \in \mathbb^\infty \left( \sum_^\infty \alpha _k = 1, \sum\limits_^\infty , \alpha_k, < \infty, \alpha_k \in \mathbb,\lambda > 0 \right).$

When all the $\alpha_k$ are non-negative, it is the discrete compound Poisson distribution (non-Poisson case) with overdispersion property.

See also

* Poisson distribution
* Zero-truncated Poisson distribution
* Compound Poisson distribution
* Sparse approximation
* Hurdle model

Software

pscl
an
brms
R packages

References

{{least squares and regression analysis

Generalized linear models
Categorical data
Poisson point processes