Zeno Machine on:
[Wikipedia]
[Google]
[Amazon]
In mathematics and
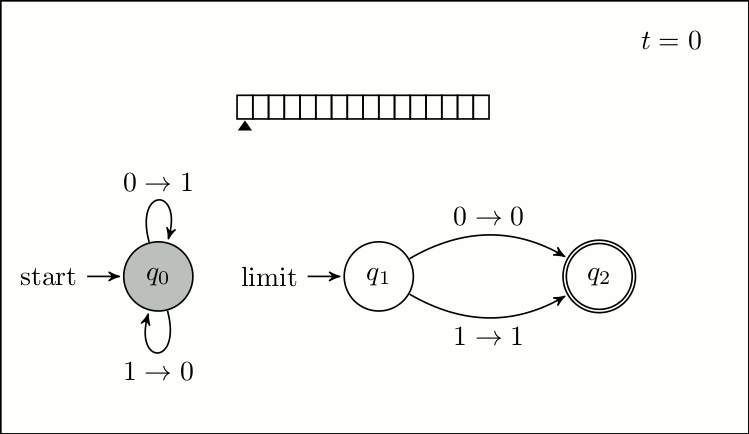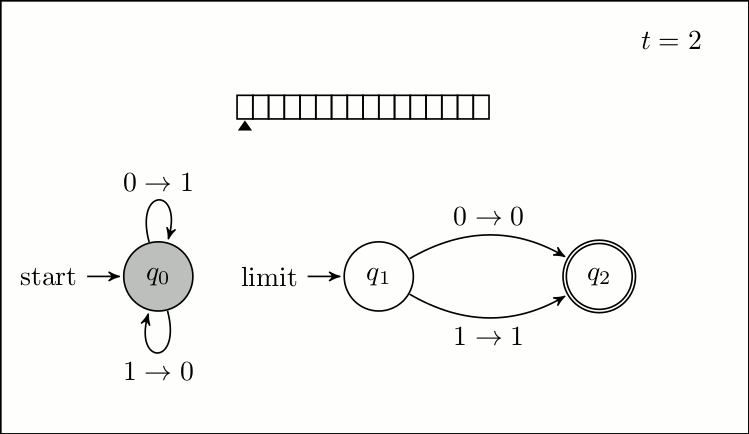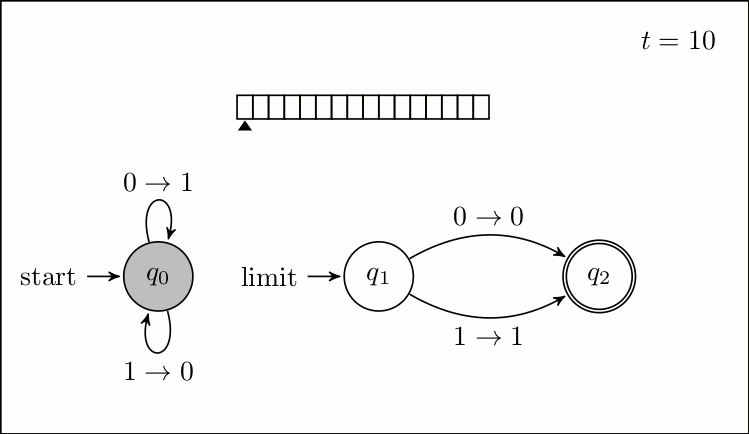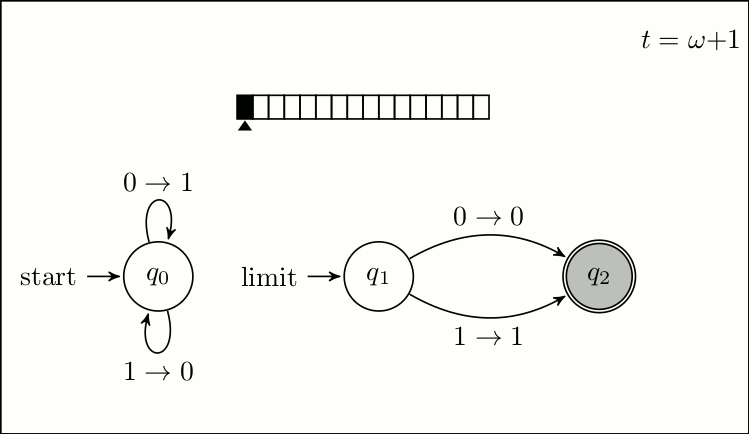 A more formal model of the Zeno machine is the infinite time Turing machine. Defined first in unpublished work by Jeffrey Kidder and expanded upon by Joel Hamkins and Andy Lewis, in ''Infinite Time Turing Machines'', the infinite time Turing machine is an extension of the classical Turing machine model, to include transfinite time; that is time beyond all finite time. A classical Turing machine has a status at step (in the start state, with an empty tape, read head at cell 0) and a procedure for getting from one status to the successive status. In this way the status of a Turing machine is defined for all steps corresponding to a natural number. An maintains these properties, but also defines the status of the machine at
A more formal model of the Zeno machine is the infinite time Turing machine. Defined first in unpublished work by Jeffrey Kidder and expanded upon by Joel Hamkins and Andy Lewis, in ''Infinite Time Turing Machines'', the infinite time Turing machine is an extension of the classical Turing machine model, to include transfinite time; that is time beyond all finite time. A classical Turing machine has a status at step (in the start state, with an empty tape, read head at cell 0) and a procedure for getting from one status to the successive status. In this way the status of a Turing machine is defined for all steps corresponding to a natural number. An maintains these properties, but also defines the status of the machine at
.
Zeno machines cannot solve their own halting problem.
computer science
Computer science is the study of computation, automation, and information. Computer science spans theoretical disciplines (such as algorithms, theory of computation, information theory, and automation) to practical disciplines (includin ...
, Zeno machines (abbreviated ZM, and also called accelerated Turing machine, ATM) are a hypothetical computational model related to Turing machines
A Turing machine is a mathematical model of computation describing an abstract machine that manipulates symbols on a strip of tape according to a table of rules. Despite the model's simplicity, it is capable of implementing any computer algori ...
that are capable of carrying out computations involving a countably infinite
In mathematics, a set is countable if either it is finite or it can be made in one to one correspondence with the set of natural numbers. Equivalently, a set is ''countable'' if there exists an injective function from it into the natural numbers ...
number of algorithmic steps. These machines are ruled out in most models of computation.
The idea of Zeno machines was first discussed by Hermann Weyl
Hermann Klaus Hugo Weyl, (; 9 November 1885 – 8 December 1955) was a German mathematician, theoretical physicist and philosopher. Although much of his working life was spent in Zürich, Switzerland, and then Princeton, New Jersey, he is ass ...
in 1927; the name refers to Zeno's paradoxes
Zeno's paradoxes are a set of philosophical problems generally thought to have been devised by Greek philosopher Zeno of Elea (c. 490–430 BC) to support Parmenides' doctrine that contrary to the evidence of one's senses, the belief in plurality ...
, attributed to the ancient Greek philosopher Zeno of Elea
Zeno of Elea (; grc, Ζήνων ὁ Ἐλεᾱ́της; ) was a pre-Socratic Greek philosopher of Magna Graecia and a member of the Eleatic School founded by Parmenides. Aristotle called him the inventor of the dialectic. He is best known ...
. Zeno machines play a crucial role in some theories. The theory of the Omega Point devised by physicist Frank J. Tipler
Frank Jennings Tipler (born February 1, 1947) is an American mathematical physicist and cosmologist, holding a joint appointment in the Departments of Mathematics and Physics at Tulane University. Tipler has written books and papers on the Omeg ...
, for instance, can only be valid if Zeno machines are possible.
Definition
A Zeno machine is a Turing machine that can take a infinite number of steps, and then continue take more steps. This can be thought of as a supertask where units of time are taken to perform the -th step; thus, the first step takes 0.5 units of time, the second takes 0.25, the third 0.125 and so on, so that after one unit of time, acountably infinite
In mathematics, a set is countable if either it is finite or it can be made in one to one correspondence with the set of natural numbers. Equivalently, a set is ''countable'' if there exists an injective function from it into the natural numbers ...
number of steps will have been performed.
Infinite Time Turing Machines
 A more formal model of the Zeno machine is the infinite time Turing machine. Defined first in unpublished work by Jeffrey Kidder and expanded upon by Joel Hamkins and Andy Lewis, in ''Infinite Time Turing Machines'', the infinite time Turing machine is an extension of the classical Turing machine model, to include transfinite time; that is time beyond all finite time. A classical Turing machine has a status at step (in the start state, with an empty tape, read head at cell 0) and a procedure for getting from one status to the successive status. In this way the status of a Turing machine is defined for all steps corresponding to a natural number. An maintains these properties, but also defines the status of the machine at
A more formal model of the Zeno machine is the infinite time Turing machine. Defined first in unpublished work by Jeffrey Kidder and expanded upon by Joel Hamkins and Andy Lewis, in ''Infinite Time Turing Machines'', the infinite time Turing machine is an extension of the classical Turing machine model, to include transfinite time; that is time beyond all finite time. A classical Turing machine has a status at step (in the start state, with an empty tape, read head at cell 0) and a procedure for getting from one status to the successive status. In this way the status of a Turing machine is defined for all steps corresponding to a natural number. An maintains these properties, but also defines the status of the machine at limit ordinals
In set theory, a limit ordinal is an ordinal number that is neither zero nor a successor ordinal. Alternatively, an ordinal λ is a limit ordinal if there is an ordinal less than λ, and whenever β is an ordinal less than λ, then there exists an ...
, that is ordinals that are neither nor the successor of any ordinal. The status of a Turing machine consists of 3 parts:
# The state
# The location of the read-write head
# The contents of the tape
Just as a classical Turing machine has a labeled start state, which is the state at the start of a program, an has a labeled ''limit'' state which is the state for the machine at any limit ordinal. This is the case even if the machine has no other way to access this state, for example no node transitions to it. The location of the read-write head is set to zero for at any limit step. Lastly the state of the tape is determined by the limit supremum of previous tape states. For some machine , a cell and, a limit ordinal then
That is the th cell at time is the limit supremum of that same cell as the machine approaches . This can be thought of as the limit if it converges or otherwise.
Computability
Zeno machines have been proposed as a model of computation more powerful than classical Turing machines, based on their ability to solve the halting problem for classical Turing machines. Cristian Calude and Ludwig Staiger present the followingpseudocode
In computer science, pseudocode is a plain language description of the steps in an algorithm or another system. Pseudocode often uses structural conventions of a normal programming language, but is intended for human reading rather than machine re ...
algorithm as a solution to the halting problem when run on a Zeno machine.
begin program
write 0 on the first position of the output tape;
begin loop
simulate 1 successive step of the given Turing machine on the given input;
if the Turing machine has halted then
write 1 on the first position of the output tape and break out of loop;
end loop
end program
By inspecting the first position of the output tape after unit of time has elapsed we can determine whether the given Turing machine halts.
In contrast Oron Shagir argues that the state of a Zeno machine is only defined on the interval See also
* Computation in the limit * Specker sequence * Ross–Littlewood paradoxReferences
{{reflist Models of computation Turing machine Hypercomputation Supertasks Articles with example pseudocode