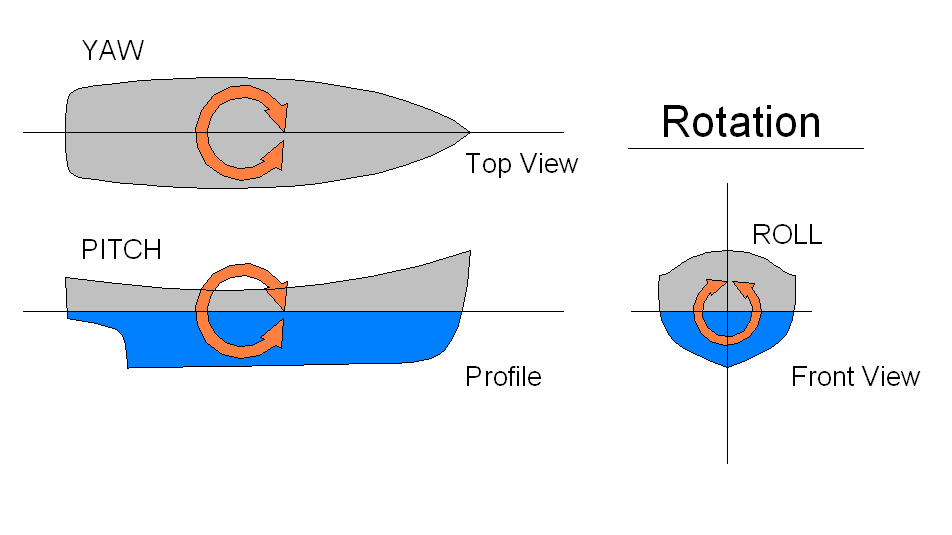
Yaw (rotation)

A yaw rotation is a movement around the yaw axis of a rigid body that changes the direction it is pointing, to the left or right of its direction of motion. The yaw rate or yaw velocity of a car, aircraft, projectile or other rigid body is the angular velocity of this rotation, or rate of change of the heading angle when the aircraft is horizontal. It is commonly measured in degrees per second or radians per second.

Another important concept is the yaw moment, or yawing moment, which is the component of a torque about the yaw axis.

Measurement

Yaw velocity can be measured by measuring the ground velocity at two geometrically separated points on the body, or by a gyroscope, or it can be synthesized from accelerometers and the like. It is the primary measure of how drivers sense a car's turning visually.

It is important in electronic stabilized vehicles. The yaw rate is directly related to the lateral acceleration of the vehicle turning at constant speed around a constant radius, by the relationship

:tangential speed*yaw velocity = lateral acceleration = tangential speed^2/radius of turn, in appropriate units

The sign convention can be established by rigorous attention to coordinate systems.

In a more general manoeuvre where the radius is varying, and/or the speed is varying, the above relationship no longer holds.

Yaw rate control

The yaw rate can be measured with accelerometers in the vertical axis. Any device intended to measure the yaw rate is called a yaw rate sensor.

Road vehicles

Studying the stability of a road vehicle requires a reasonable approximation to the equations of motion.

The diagram illustrates a four-wheel vehicle, in which the front axle is located ''a'' metres ahead of the centre of gravity and the rear axle is ''b'' metres towards the rear from the center of gravity. The body of the car is pointing in a direction $\theta$ (theta) while it is travelling in a direction $\psi$ (psi). In general, these are not the same. The tyre treads at the region of contact point in the direction of travel, but the hubs are aligned with the vehicle body, with the steering held central. The tyres distort as they rotate to accommodate this mis-alignment, and generate side forces as a consequence.

From directional stability study, denoting the angular velocity $\omega$, the equations of motion are:

:$\frac=2k\frac\beta-2k\frac\omega$
:$\frac=-\frac\beta+(1-2k)\frac\omega$

with $M$ the mass of the vehicle, $V$ the vehicle speed and $\beta = \theta - \psi$ the vehicle's overall angle.

The coefficient of $\frac$ will be called the ' damping' by analogy with a mass-spring-damper which has a similar equation of motion. By the same analogy, the coefficient of $\beta$ will be called the 'stiffness', as its function is to return the system to zero deflection, in the same manner as a spring.

The form of the solution depends only on the signs of the damping and stiffness terms. The four possible solution types are presented in the figure.

The only satisfactory solution requires both stiffness and damping to be positive. If the centre of gravity is ahead of the centre of the wheelbase $(b>a)$, this will always be positive, and the vehicle will be stable at all speeds. However, if it lies further aft, the term has the potential of becoming negative above a speed given by:

::$V^2=\frac$

Above this speed, the vehicle will be directionally (yaw) unstable. Corrections for relative effect of front and rear tyres and steering forces are available in the main article.

Relationship with other rotation systems

These rotations are intrinsic rotations and the calculus behind them is similar to the Frenet-Serret formulas. Performing a rotation in an intrinsic reference frame is equivalent to right-multiply its characteristic matrix (the matrix that has the vector of the reference frame as columns) by the matrix of the rotation.

History

The first aircraft to demonstrate active control about all three axes was the Wright brothers' 1902 glider.{{cite web , url=https://www.grc.nasa.gov/WWW/K-12/airplane/rotations.html , title=Aircraft rotations , date=2015-05-05 , publisher=Glenn Research Center , access-date=2018-10-13

See also

* Adverse yaw
* Aircraft principal axes
* Coriolis acceleration
* Directional stability
* Flight dynamics
* Six degrees of freedom
* Vehicle dynamics
* Yaw rate sensor

References

Dynamics (mechanics)
Attitude control