Visco-elastic Jets

Visco-elastic jets are the jets of viscoelastic fluids, i.e. fluids that disobey Newton's law of Viscocity. A Viscoelastic fluid that returns to its original shape after the applied stress is released.

Everybody has witnessed a situation where a liquid is poured out of an orifice at a given height and speed, and it hits a solid surface. For example, – dropping of honey onto a bread slice, or pouring shower gel onto one's hand. Honey is a purely viscous, Newtonian fluid: the jet thins continuously and coils regularly.

Jets of non-Newtonian Viscoelastic fluids show a novel behaviour. A viscoelastic jet breaks up much more slowly than a Newtonian jet. Typically, it evolves into the so-called beads-on-string structure, where large drops are connected by thin threads. The jet widens at its base (reverse swell phenomenon) and folds back and forth on itself. The slow breakup process provides the viscoelastic jet sufficient time to exhibit some new phenomena, including drop migration, drop oscillation, drop merging and drop draining.

These properties are a result of the interplay of non-Newtonian properties (viscoelasticity, shear-thinning) with gravitational, viscous, and inertial effects in the jets.
Free surface continuous jets of viscoelastic fluids are relevant in many engineering applications involving blood, paints, adhesives or foodstuff and industrial processes like fiber spinning, bottle-filling, oil drilling etc. In many of these processes, an understanding of the instabilities a jet undergoes due to changes in fluid parameters like Reynolds number or Deborah number is essential from process engineering point of view. With the advent of microfluidics, an understanding of the jetting properties of non-Newtonian fluids becomes essential from micro- to macro length scales, and from low to high Reynolds numbers7–9. Like other fluids, When considering viscoelastic flows, the velocity, pressure and stress must satisfy the mass and momentum equation, supplemented with a constitutive equation involving the velocity and stress.

The temporal evolution of a viscoelastic fluid thread depends on the relative magnitude of the viscous, inertial, and elastic stresses and the capillary pressure. To study the inertio-elasto-capillary balance for a jet, two dimensionless parameters are defined: the Ohnesorge number (Oℎ)
:$Oh=\frac$
, which is the inverse of the Reynolds number based on a characteristic capillary velocity $\frac$ and, secondly, the intrinsic Deborah number De,
:$De = \lambda \sqrt[]$
, defined as the ratio of the time scale for elastic stress relaxation, λ, to the “Rayleigh time scale” for inertio-capillary breakup of an inviscid jet, $t_r=\sqrt[]$. In these expressions, $\rho$ is the fluid density, $\eta_0$ is the fluid zero shear viscosity, $\gamma$ is the surface tension, $R_0$ is the initial radius of the jet, and $\lambda$ is the relaxation time associated with the polymer solution.

Mathematical Equations governing bead formation, filament thinning & breakup in weakly viscoelastic jets

, where (z, t) is the axial velocity; $\eta_s$ and $\eta_p$ are the solvent and polymer contribution to the total viscosity, respectively (total viscosity $\eta_0=\eta_s+\eta_p$); $R_z$ indicates the partial derivative $\frac$ ; $\sigma_$ and $\sigma_$ are the diagonal terms of the extra-stress tensor. Equation (1) represents mass conservation, Equation (2) represents momentum equation in one dimension. Extra stress tensors $\sigma_$ and $\sigma_$ can be calculated as follows:

, where $\lambda$ is the relaxation time of the liquid; $\alpha$ is a positive dimensionless parameter corresponding to the anisotropy of the hydrodynamic drag on the polymer molecules and is called the mobility factor

{{-

Beads on string structure

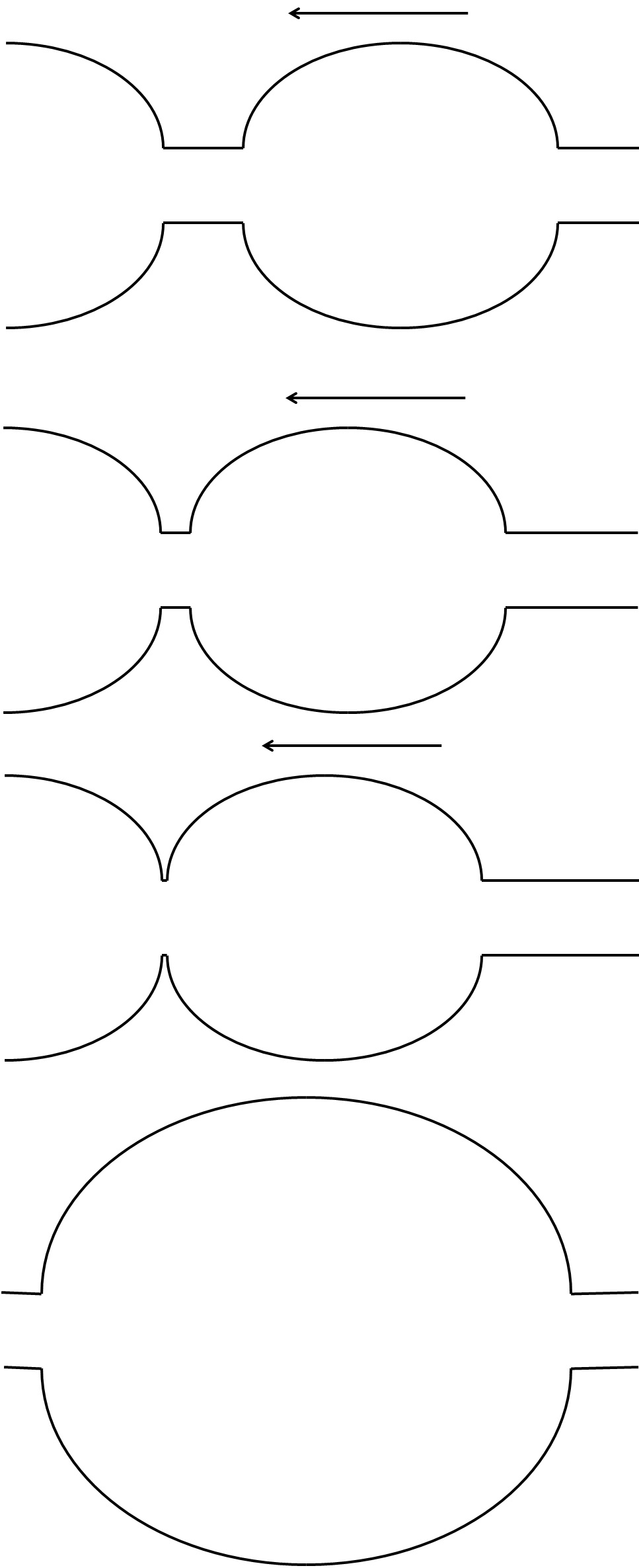
Drop Draining

In drop draining a small bead between two beads gets smaller in size and the fluid particle moves towards the adjacent beads. The smaller bead drains out as shown in the figure.

Drop Merging

In drop merging, a smaller bead and a larger bead move close to each other and merge to form a single bead.

Drop Collision

In drop collision, two adjacent beads collide to form a single bead.

Drop Oscillation

In drop oscillation, two adjacent beads start oscillating and eventually the distance between them decreases. After sometime they merge to form a single bead.

References

# http://www2.eng.cam.ac.uk/~jl305/VisJet/recoil_mv.gif
# http://www2.eng.cam.ac.uk/~jl305/VisJet/merging.gif
# http://www2.eng.cam.ac.uk/~jl305/VisJet/collison.gif
# http://www2.eng.cam.ac.uk/~jl305/VisJet/oscil.gif
# http://www2.eng.cam.ac.uk/~jl305/VisJet/draining.gif
# http://www2.eng.cam.ac.uk/~jl305/VisJet/dropdyn.html
# http://web.mit.edu/nnf/research/phenomena/viscoelastic_jet.html

Elasticity (physics)
Non-Newtonian fluids