Vertical Subspace

In mathematics, the vertical bundle and the horizontal bundle are vector bundles associated to a smooth fiber bundle. More precisely, given a smooth fiber bundle $\pi\colon E\to B$, the vertical bundle $VE$ and horizontal bundle $HE$ are subbundles of the tangent bundle $TE$ of $E$ whose Whitney sum satisfies $VE\oplus HE\cong TE$. This means that, over each point $e\in E$, the fibers $V_eE$ and $H_eE$ form complementary subspaces of the tangent space $T_eE$. The vertical bundle consists of all vectors that are tangent to the fibers, while the horizontal bundle requires some choice of complementary subbundle.

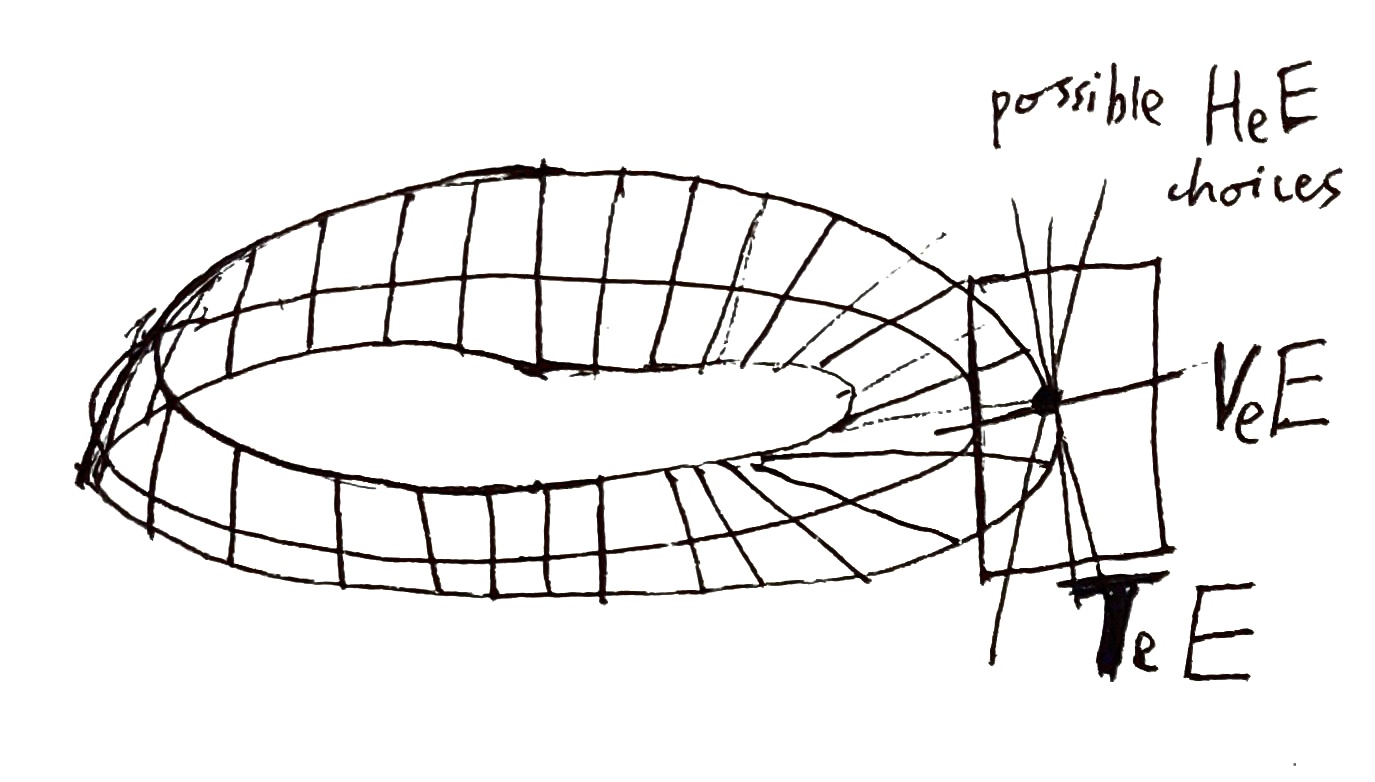
To make this precise, define the vertical space $V_eE$ at $e\in E$ to be $\ker(d\pi_e)$. That is, the differential $d\pi_e\colon T_eE\to T_bB$ (where $b=\pi(e)$) is a linear surjection whose kernel has the same dimension as the fibers of $\pi$. If we write $F=\pi^(b)$, then $V_eE$ consists of exactly the vectors in $T_eE$ which are also tangent to $F$. The name is motivated by low-dimensional examples like the trivial line bundle over a circle, which is sometimes depicted as a vertical cylinder projecting to a horizontal circle. A subspace $H_eE$ of $T_eE$ is called a horizontal space if $T_eE$ is the direct sum of $V_eE$ and $H_eE$.

The disjoint union of the vertical spaces V_''e''''E'' for each ''e'' in ''E'' is the subbundle V''E'' of T''E;'' this is the vertical bundle of ''E''. Likewise, provided the horizontal spaces $H_eE$ vary smoothly with ''e'', their disjoint union is a horizontal bundle. The use of the words "the" and "a" here is intentional: each vertical subspace is unique, defined explicitly by $\ker(d\pi_e)$. Excluding trivial cases, there are an infinite number of horizontal subspaces at each point. Also note that arbitrary choices of horizontal space at each point will not, in general, form a smooth vector bundle; they must also vary in an appropriately smooth way.

The horizontal bundle is one way to formulate the notion of an Ehresmann connection on a fiber bundle. Thus, for example, if ''E'' is a principal ''G''-bundle, then the horizontal bundle is usually required to be ''G''-invariant: such a choice is equivalent to a connection on the principal bundle.David Bleecker,
Gauge Theory and Variational Principles
' (1981) Addison-Wesely Publishing Company ''(See theorem 1.2.4)'' This notably occurs when ''E'' is the frame bundle associated to some vector bundle, which is a principal $\operatorname_n$ bundle.

Formal definition

Let ''π'':''E''→''B'' be a smooth fiber bundle over a smooth manifold ''B''. The vertical bundle is the kernel V''E'' := ker(d''π'') of the tangent map d''π'' : T''E'' → T''B''. (page 77)

Since dπ_e is surjective at each point ''e'', it yields a ''regular'' subbundle of T''E''. Furthermore, the vertical bundle V''E'' is also integrable.

An Ehresmann connection on ''E'' is a choice of a complementary subbundle H''E'' to V''E'' in T''E'', called the horizontal bundle of the connection. At each point ''e'' in ''E'', the two subspaces form a direct sum, such that
T_''e''''E'' = V_''e''''E'' ⊕ H_''e''''E''.

Example

A simple example of a smooth fiber bundle is a Cartesian product of two manifolds. Consider the bundle ''B''₁ := (''M'' × ''N'', pr₁) with bundle projection pr₁ : ''M'' × ''N'' → ''M'' : (''x'', ''y'') → ''x''. Applying the definition in the paragraph above to find the vertical bundle, we consider first a point (m,n) in ''M'' × ''N''. Then the image of this point under pr₁ is m. The preimage of m under this same pr₁ is × ''N'', so that T_(m,n) ( × ''N'') = × T''N''. The vertical bundle is then V''B''₁ = ''M'' × T''N'', which is a subbundle of T(''M'' ×''N''). If we take the other projection pr₂ : ''M'' × ''N'' → ''N'' : (''x'', ''y'') → ''y'' to define the fiber bundle ''B''₂ := (''M'' × ''N'', pr₂) then the vertical bundle will be V''B''₂ = T''M'' × ''N''.

In both cases, the product structure gives a natural choice of horizontal bundle, and hence an Ehresmann connection: the horizontal bundle of ''B''₁ is the vertical bundle of ''B''₂ and vice versa.

Properties

Various important tensors and differential forms from differential geometry take on specific properties on the vertical and horizontal bundles, or even can be defined in terms of them. Some of these are:

* A vertical vector field is a vector field that is in the vertical bundle. That is, for each point ''e'' of ''E'', one chooses a vector $v_e\in V_eE$ where $V_eE \subset T_eE = T_e(E_ )$ is the vertical vector space at ''e''.
* A differentiable r-form $\alpha$ on ''E'' is said to be a horizontal form if $\alpha(v_1,...,v_r)=0$ whenever at least one of the vectors $v_1,..., v_r$ is vertical.
* The connection form vanishes on the horizontal bundle, and is non-zero only on the vertical bundle. In this way, the connection form can be used to define the horizontal bundle: The horizontal bundle is the kernel of the connection form.
* The solder form or tautological one-form vanishes on the vertical bundle and is non-zero only on the horizontal bundle. By definition, the solder form takes its values entirely in the horizontal bundle.
* For the case of a frame bundle, the torsion form vanishes on the vertical bundle, and can be used to define exactly that part that needs to be added to an arbitrary connection to turn it into a Levi-Civita connection, i.e. to make a connection be torsionless. Indeed, if one writes θ for the solder form, then the torsion tensor Θ is given by Θ = D θ (with D the exterior covariant derivative). For any given connection ω, there is a ''unique'' one-form σ on T''E'', called the contorsion tensor, that is vanishing in the vertical bundle, and is such that ω+σ is another connection 1-form that is torsion-free. The resulting one-form ω+σ is nothing other than the Levi-Civita connection. One can take this as a definition: since the torsion is given by $\Theta = D\theta = d\theta + \omega \wedge \theta$, the vanishing of the torsion is equivalent to having $d\theta = - (\omega +\sigma) \wedge \theta$, and it is not hard to show that σ must vanish on the vertical bundle, and that σ must be ''G''-invariant on each fibre (more precisely, that σ transforms in the adjoint representation of ''G''). Note that this defines the Levi-Civita connection without making any explicit reference to any metric tensor (although the metric tensor can be understood to be a special case of a solder form, as it establishes a mapping between the tangent and cotangent bundles of the base space, i.e. between the horizontal and vertical subspaces of the frame bundle).
* In the case where ''E'' is a principal bundle, then the fundamental vector field must necessarily live in the vertical bundle, and vanish in any horizontal bundle.

Notes

References

*
*
*
*
* {{citation, last1 = Saunders, first1 = D.J., title = The geometry of jet bundles, year = 1989, publisher = Cambridge University Press, isbn = 0-521-36948-7, url-access = registration, url = https://archive.org/details/geometryofjetbun0000saun

Differential topology
Fiber bundles
Connection (mathematics)