Verhulst Equation

A logistic function or logistic curve is a common S-shaped curve ( sigmoid curve) with equation

$f(x) = \frac,$

where

For values of $x$ in the domain of real numbers from $-\infty$ to $+\infty$, the S-curve shown on the right is obtained, with the graph of $f$ approaching $L$ as $x$ approaches $+\infty$ and approaching zero as $x$ approaches $-\infty$.

The logistic function finds applications in a range of fields, including biology (especially ecology), biomathematics, chemistry, demography, economics, geoscience, mathematical psychology, probability, sociology, political science, linguistics, statistics, and artificial neural networks. A generalization of the logistic function is the hyperbolastic function of type I.

The standard logistic function, where $L=1,k=1,x_0=0$, is sometimes simply called ''the sigmoid''. It is also sometimes called the ''expit'', being the inverse of the logit.

History

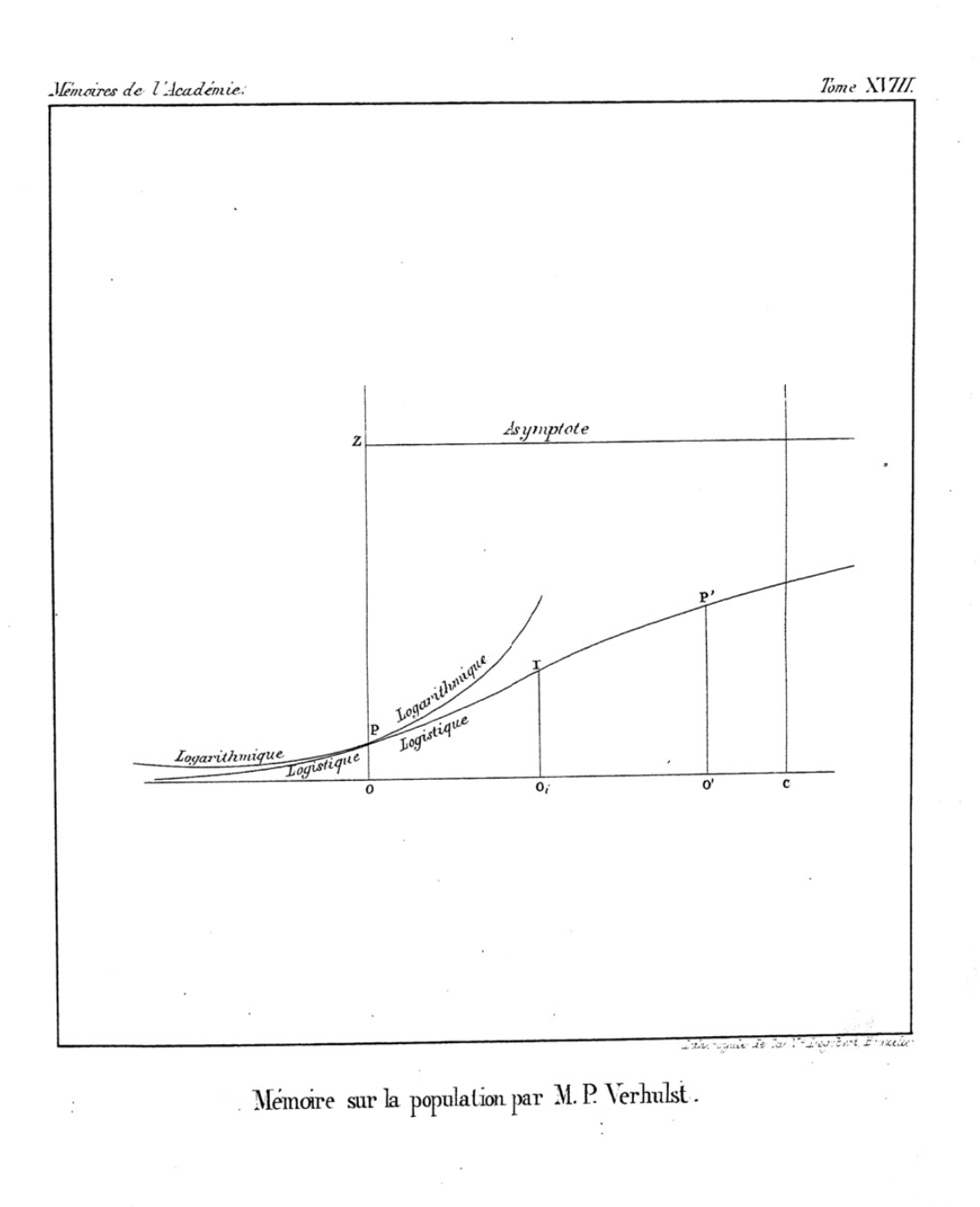
The logistic function was introduced in a series of three papers by Pierre François Verhulst between 1838 and 1847, who devised it as a model of population growth by adjusting the exponential growth model, under the guidance of Adolphe Quetelet. Verhulst first devised the function in the mid 1830s, publishing a brief note in 1838, then presented an expanded analysis and named the function in 1844 (published 1845); the third paper adjusted the correction term in his model of Belgian population growth.

The initial stage of growth is approximately exponential (geometric); then, as saturation begins, the growth slows to linear (arithmetic), and at maturity, growth stops. Verhulst did not explain the choice of the term "logistic" (french: link=no, logistique), but it is presumably in contrast to the ''logarithmic'' curve, and by analogy with arithmetic and geometric. His growth model is preceded by a discussion of arithmetic growth and geometric growth (whose curve he calls a logarithmic curve, instead of the modern term exponential curve), and thus "logistic growth" is presumably named by analogy, ''logistic'' being from grc, λογῐστῐκός, logistikós, a traditional division of Greek mathematics. The term is unrelated to the military and management term ''logistics'', which is instead from french: "lodgings", though some believe the Greek term also influenced ''logistics''; see for details.

Mathematical properties

The is the logistic function with parameters $k = 1$, $x_0 = 0$, $L = 1$, which yields

$f(x) = \frac = \frac = \frac12 + \frac12 \tanh\left(\frac\right).$

In practice, due to the nature of the exponential function $e^$, it is often sufficient to compute the standard logistic function for $x$ over a small range of real numbers, such as a range contained in ��6, +6 as it quickly converges very close to its saturation values of 0 and 1.

The logistic function has the symmetry property that

$1 - f(x) = f(-x).$

Thus, $x \mapsto f(x) - 1/2$ is an odd function.

The logistic function is an offset and scaled hyperbolic tangent function:
$f(x) = \frac12 + \frac12 \tanh\left(\frac\right),$
or
$\tanh(x) = 2 f(2x) - 1.$

This follows from
$\begin \tanh(x) & = \frac = \frac \\ &= f(2x) - \frac = f(2x) - \frac = 2f(2x) - 1. \end$

Derivative

The standard logistic function has an easily calculated derivative. The derivative is known as the density of the logistic distribution:
$f(x) = \frac = \frac,$
$\fracf(x) = \frac = \frac = f(x)\big(1 - f(x)\big)$

The logistic distribution has mean ''x''₀ and variance ''π''/3''k''

Integral

Conversely, its antiderivative can be computed by the substitution $u = 1 + e^x$, since $f(x) = \frac = \frac$, so (dropping the constant of integration)

$\int \frac\,dx = \int \frac\,du = \ln u = \ln (1 + e^x).$

In artificial neural networks, this is known as the '' softplus'' function and (with scaling) is a smooth approximation of the ramp function, just as the logistic function (with scaling) is a smooth approximation of the Heaviside step function.

Logistic differential equation

The standard logistic function is the solution of the simple first-order non-linear ordinary differential equation

$\fracf(x) = f(x)\big(1 - f(x)\big)$

with boundary condition $f(0) = 1/2$. This equation is the continuous version of the logistic map. Note that the reciprocal logistic function is solution to a simple first-order ''linear'' ordinary differential equation.

The qualitative behavior is easily understood in terms of the phase line: the derivative is 0 when the function is 1; and the derivative is positive for $f$ between 0 and 1, and negative for $f$ above 1 or less than 0 (though negative populations do not generally accord with a physical model). This yields an unstable equilibrium at 0 and a stable equilibrium at 1, and thus for any function value greater than 0 and less than 1, it grows to 1.

The logistic equation is a special case of the Bernoulli differential equation and has the following solution:

$f(x) = \frac.$

Choosing the constant of integration $C = 1$ gives the other well known form of the definition of the logistic curve:

$f(x) = \frac = \frac.$

More quantitatively, as can be seen from the analytical solution, the logistic curve shows early exponential growth for negative argument, which reaches to linear growth of slope 1/4 for an argument near 0, then approaches 1 with an exponentially decaying gap.

The logistic function is the inverse of the natural logit function

: \operatorname p = \log \frac p \text 0

and so converts the logarithm of odds into a probability. The conversion from the log-likelihood ratio of two alternatives also takes the form of a logistic curve.

The differential equation derived above is a special case of a general differential equation that only models the sigmoid function for $x > 0$. In many modeling applications, the more ''general form''
$\frac = \frac f(x)\big(a - f(x)\big), \quad f(0) = \frac a$
can be desirable. Its solution is the shifted and scaled sigmoid $aS\big(k(x - r)\big)$.

The hyperbolic-tangent relationship leads to another form for the logistic function's derivative:

$\frac f(x) = \frac14 \operatorname^2\left(\frac\right),$

which ties the logistic function into the logistic distribution.

Rotational symmetry about (0, 1/2)

The sum of the logistic function and its reflection about the vertical axis, $f(-x)$, is

$\frac + \frac = \frac + \frac = 1.$

The logistic function is thus rotationally symmetrical about the point (0, 1/2).

Applications

LinkS. W. Link, Psychometrika, 1975, 40, 1, 77–105 created an extension of Wald's theory of sequential analysis to a distribution-free accumulation of random variables until either a positive or negative bound is first equaled or exceeded. LinkS. W. Link, Attention and Performance VII, 1978, 619–630 derives the probability of first equaling or exceeding the positive boundary as $1/(1+e^)$, the logistic function. This is the first proof that the logistic function may have a stochastic process as its basis. LinkS. W. Link, The wave theory of difference and similarity (book), Taylor and Francis, 1992 provides a century of examples of "logistic" experimental results and a newly derived relation between this probability and the time of absorption at the boundaries.

In ecology: modeling population growth

A typical application of the logistic equation is a common model of population growth (see also population dynamics), originally due to Pierre-François Verhulst in 1838, where the rate of reproduction is proportional to both the existing population and the amount of available resources, all else being equal. The Verhulst equation was published after Verhulst had read Thomas Malthus' ''An Essay on the Principle of Population'', which describes the Malthusian growth model of simple (unconstrained) exponential growth. Verhulst derived his logistic equation to describe the self-limiting growth of a biological population. The equation was rediscovered in 1911 by A. G. McKendrick for the growth of bacteria in broth and experimentally tested using a technique for nonlinear parameter estimation. The equation is also sometimes called the ''Verhulst-Pearl equation'' following its rediscovery in 1920 by Raymond Pearl (1879–1940) and Lowell Reed (1888–1966) of the Johns Hopkins University. Another scientist, Alfred J. Lotka derived the equation again in 1925, calling it the ''law of population growth''.

Letting $P$ represent population size ($N$ is often used in ecology instead) and $t$ represent time, this model is formalized by the differential equation:

$\frac=r P \left(1 - \frac\right),$

where the constant $r$ defines the growth rate and $K$ is the carrying capacity.

In the equation, the early, unimpeded growth rate is modeled by the first term $+rP$. The value of the rate $r$ represents the proportional increase of the population $P$ in one unit of time. Later, as the population grows, the modulus of the second term (which multiplied out is $-r P^2 / K$) becomes almost as large as the first, as some members of the population $P$ interfere with each other by competing for some critical resource, such as food or living space. This antagonistic effect is called the ''bottleneck'', and is modeled by the value of the parameter $K$. The competition diminishes the combined growth rate, until the value of $P$ ceases to grow (this is called ''maturity'' of the population).
The solution to the equation (with $P_0$ being the initial population) is

$P(t) = \frac = \frac,$

where

$\lim_ P(t) = K,$

where $K$ is the limiting value of $P$, the highest value that the population can reach given infinite time (or come close to reaching in finite time). It is important to stress that the carrying capacity is asymptotically reached independently of the initial value $P(0) > 0$, and also in the case that $P(0) > K$.

In ecology, species are sometimes referred to as $r$-strategist or $K$-strategist depending upon the selective processes that have shaped their life history strategies.
Choosing the variable dimensions so that $n$ measures the population in units of carrying capacity, and $\tau$ measures time in units of $1/r$, gives the dimensionless differential equation

$\frac = n (1-n).$

Time-varying carrying capacity

Since the environmental conditions influence the carrying capacity, as a consequence it can be time-varying, with $K(t) > 0$, leading to the following mathematical model:

$\frac = rP \cdot \left(1 - \frac\right).$

A particularly important case is that of carrying capacity that varies periodically with period $T$:

$K(t + T) = K(t).$

It can be shown that in such a case, independently from the initial value $P(0) > 0$, $P(t)$ will tend to a unique periodic solution $P_*(t)$, whose period is $T$.

A typical value of $T$ is one year: In such case $K(t)$ may reflect periodical variations of weather conditions.

Another interesting generalization is to consider that the carrying capacity $K(t)$ is a function of the population at an earlier time, capturing a delay in the way population modifies its environment. This leads to a logistic delay equation, which has a very rich behavior, with bistability in some parameter range, as well as a monotonic decay to zero, smooth exponential growth, punctuated unlimited growth (i.e., multiple S-shapes), punctuated growth or alternation to a stationary level, oscillatory approach to a stationary level, sustainable oscillations, finite-time singularities as well as finite-time death.

In statistics and machine learning

Logistic functions are used in several roles in statistics. For example, they are the cumulative distribution function of the logistic family of distributions, and they are, a bit simplified, used to model the chance a chess player has to beat their opponent in the Elo rating system. More specific examples now follow.

Logistic regression

Logistic functions are used in logistic regression to model how the probability $p$ of an event may be affected by one or more explanatory variables: an example would be to have the model

$p = f(a + bx),$

where $x$ is the explanatory variable, $a$ and $b$ are model parameters to be fitted, and $f$ is the standard logistic function.

Logistic regression and other log-linear models are also commonly used in machine learning. A generalisation of the logistic function to multiple inputs is the softmax activation function, used in multinomial logistic regression.

Another application of the logistic function is in the Rasch model, used in item response theory. In particular, the Rasch model forms a basis for maximum likelihood estimation of the locations of objects or persons on a continuum, based on collections of categorical data, for example the abilities of persons on a continuum based on responses that have been categorized as correct and incorrect.

Neural networks

Logistic functions are often used in neural networks to introduce nonlinearity in the model or to clamp signals to within a specified interval. A popular neural net element computes a linear combination of its input signals, and applies a bounded logistic function as the activation function to the result; this model can be seen as a "smoothed" variant of the classical threshold neuron.

A common choice for the activation or "squashing" functions, used to clip for large magnitudes to keep the response of the neural network boundedGershenfeld 1999, p. 150. is

$g(h) = \frac,$

which is a logistic function.

These relationships result in simplified implementations of artificial neural networks with artificial neurons. Practitioners caution that sigmoidal functions which are antisymmetric about the origin (e.g. the hyperbolic tangent) lead to faster convergence when training networks with backpropagation.

The logistic function is itself the derivative of another proposed activation function, the softplus.

In medicine: modeling of growth of tumors

Another application of logistic curve is in medicine, where the logistic differential equation is used to model the growth of tumors. This application can be considered an extension of the above-mentioned use in the framework of ecology (see also the Generalized logistic curve, allowing for more parameters). Denoting with $X(t)$ the size of the tumor at time $t$, its dynamics are governed by

$X' = r\left(1 - \frac X K \right)X,$

which is of the type

$X' = F(X)X, \quad F'(X) \le 0,$

where $F(X)$ is the proliferation rate of the tumor.

If a chemotherapy is started with a log-kill effect, the equation may be revised to be

$X' = r\left(1 - \frac X K \right)X - c(t) X,$

where $c(t)$ is the therapy-induced death rate. In the idealized case of very long therapy, $c(t)$ can be modeled as a periodic function (of period $T$) or (in case of continuous infusion therapy) as a constant function, and one has that

$\frac 1 T \int_0^T c(t)\, dt > r \to \lim_ x(t) = 0,$

i.e. if the average therapy-induced death rate is greater than the baseline proliferation rate, then there is the eradication of the disease. Of course, this is an oversimplified model of both the growth and the therapy (e.g. it does not take into account the phenomenon of clonal resistance).

In medicine: modeling of a pandemic

A novel infectious pathogen to which a population has no immunity will generally spread exponentially in the early stages, while the supply of susceptible individuals is plentiful. The SARS-CoV-2 virus that causes COVID-19 exhibited exponential growth early in the course of infection in several countries in early 2020. Factors including a lack of susceptible hosts (through the continued spread of infection until it passes the threshold for herd immunity) or reduction in the accessibility of potential hosts through physical distancing measures, may result in exponential-looking epidemic curves first linearizing (replicating the "logarithmic" to "logistic" transition first noted by Pierre-François Verhulst, as noted above) and then reaching a maximal limit.

A logistic function, or related functions (e.g. the Gompertz function) are usually used in a descriptive or phenomenological manner because they fit well not only to the early exponential rise, but to the eventual levelling off of the pandemic as the population develops a herd immunity. This is in contrast to actual models of pandemics which attempt to formulate a description based on the dynamics of the pandemic (e.g. contact rates, incubation times, social distancing, etc.). Some simple models have been developed, however, which yield a logistic solution.

Modeling early COVID-19 cases

A generalized logistic function, also called the Richards growth curve, has been applied to model the early phase of the COVID-19 outbreak. The authors fit the generalized logistic function to the cumulative number of infected cases, here referred to as ''infection trajectory''. There are different parameterizations of the generalized logistic function in the literature. One frequently used forms is

$f(t ; \theta_1,\theta_2,\theta_3, \xi) = \frac$

where $\theta_1,\theta_2,\theta_3$ are real numbers, and $\xi$ is a positive real number. The flexibility of the curve $f$ is due to the parameter $\xi$: (i) if $\xi = 1$ then the curve reduces to the logistic function, and (ii) as $\xi$ approaches zero, the curve converges to the Gompertz function. In epidemiological modeling, $\theta_1$, $\theta_2$, and $\theta_3$ represent the final epidemic size, infection rate, and lag phase, respectively. See the right panel for an example infection trajectory when $(\theta_1,\theta_2,\theta_3)$ is set to $(10000,0.2,40)$.

One of the benefits of using a growth function such as the generalized logistic function in epidemiological modeling is its relatively easy application to the multilevel model framework, where information from different geographic regions can be pooled together.

In chemistry: reaction models

The concentration of reactants and products in autocatalytic reactions follow the logistic function.
The degradation of Platinum group metal-free (PGM-free) oxygen reduction reaction (ORR) catalyst in fuel cell cathodes follows the logistic decay function, suggesting an autocatalytic degradation mechanism.

In physics: Fermi–Dirac distribution

The logistic function determines the statistical distribution of fermions over the energy states of a system in thermal equilibrium. In particular, it is the distribution of the probabilities that each possible energy level is occupied by a fermion, according to Fermi–Dirac statistics.

In material science: Phase diagrams

See Diffusion bonding.

In linguistics: language change

In linguistics, the logistic function can be used to model language change:Bod, Hay, Jennedy (eds.) 2003, pp. 147–156 an innovation that is at first marginal begins to spread more quickly with time, and then more slowly as it becomes more universally adopted.

In agriculture: modeling crop response

The logistic S-curve can be used for modeling the crop response to changes in growth factors. There are two types of response functions: ''positive'' and ''negative'' growth curves. For example, the crop yield may ''increase'' with increasing value of the growth factor up to a certain level (positive function), or it may ''decrease'' with increasing growth factor values (negative function owing to a negative growth factor), which situation requires an ''inverted'' S-curve.

In economics and sociology: diffusion of innovations

The logistic function can be used to illustrate the progress of the diffusion of an innovation through its life cycle.

In ''The Laws of Imitation'' (1890), Gabriel Tarde describes the rise and spread of new ideas through imitative chains. In particular, Tarde identifies three main stages through which innovations spread: the first one corresponds to the difficult beginnings, during which the idea has to struggle within a hostile environment full of opposing habits and beliefs; the second one corresponds to the properly exponential take-off of the idea, with $f(x)=2^x$; finally, the third stage is logarithmic, with $f(x)=\log(x)$, and corresponds to the time when the impulse of the idea gradually slows down while, simultaneously new opponent ideas appear. The ensuing situation halts or stabilizes the progress of the innovation, which approaches an asymptote.

In a Sovereign state, the subnational units (constituent states or cities) may use loans to finance their projects. However, this funding source is usually subject to strict legal rules as well as to economy scarcity constraints, specially the resources the banks can lend (due to their equity or Basel limits). These restrictions, which represent a saturation level, along with an exponential rush in an economic competition for money, create a public finance diffusion of credit pleas and the aggregate national response is a sigmoid curve.

In the history of economy, when new products are introduced there is an intense amount of research and development which leads to dramatic improvements in quality and reductions in cost. This leads to a period of rapid industry growth. Some of the more famous examples are: railroads, incandescent light bulbs, electrification, cars and air travel. Eventually, dramatic improvement and cost reduction opportunities are exhausted, the product or process are in widespread use with few remaining potential new customers, and markets become saturated.

Logistic analysis was used in papers by several researchers at the International Institute of Applied Systems Analysis ( IIASA). These papers deal with the diffusion of various innovations, infrastructures and energy source substitutions and the role of work in the economy as well as with the long economic cycle. Long economic cycles were investigated by Robert Ayres (1989). Cesare Marchetti published on long economic cycles and on diffusion of innovations. Arnulf Grübler's book (1990) gives a detailed account of the diffusion of infrastructures including canals, railroads, highways and airlines, showing that their diffusion followed logistic shaped curves.

Carlota Perez used a logistic curve to illustrate the long (Kondratiev) business cycle with the following labels: beginning of a technological era as ''irruption'', the ascent as ''frenzy'', the rapid build out as ''synergy'' and the completion as ''maturity''.

See also

* Cross fluid
* Diffusion of innovations
* Exponential growth
* Hyperbolic growth
* Generalised logistic function
* Gompertz curve
* Heaviside step function
* Hill equation (biochemistry)
* Hubbert curve
* List of mathematical functions
* Logistic distribution
* Logistic map
* Logistic regression
* Logistic smooth-transmission model
* Logit
* Log-likelihood ratio
* Malthusian growth model
* Michaelis–Menten equation
* Population dynamics
* ''r''/''K'' selection theory
* Rectifier (neural networks)
* Shifted Gompertz distribution
* Tipping point (sociology)

Notes

References

*
** Published as:
*
*
*
*

External links

* L.J. Linacre
Why logistic ogive and not autocatalytic curve?
accessed 2009-09-12.
* https://web.archive.org/web/20060914155939/http://luna.cas.usf.edu/~mbrannic/files/regression/Logistic.html
* {{MathWorld , title=Sigmoid Function , urlname= SigmoidFunction

Online experiments with JSXGraph



Seeing the s-curve is everything.

Restricted Logarithmic Growth with Injection

Special functions
Differential equations
Population
Population ecology
Logistic regression
Growth curves