Truncated Hexagonal Tiling

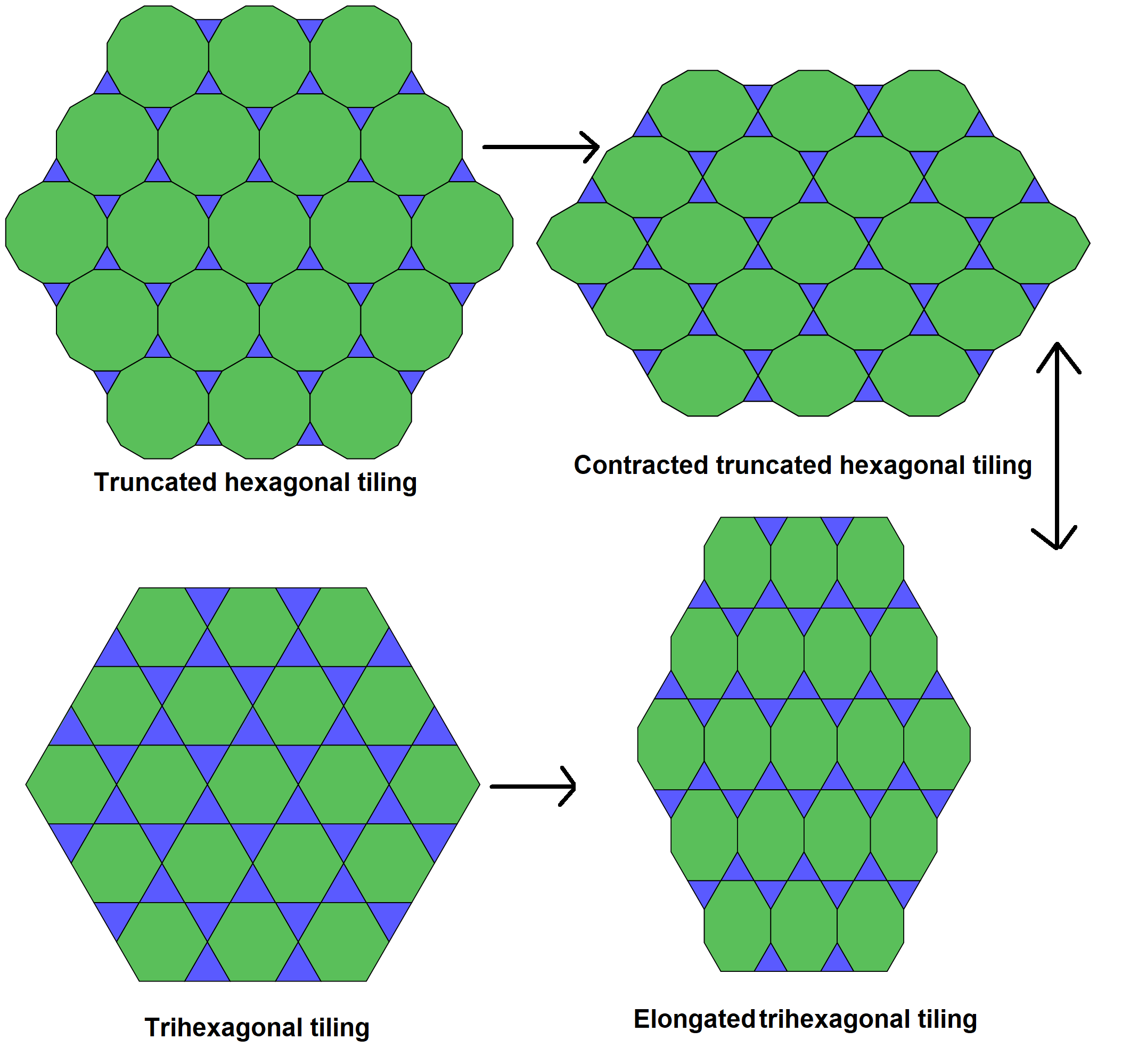
In geometry, the truncated hexagonal tiling is a semiregular tiling of the Euclidean plane. There are 2 dodecagons (12-sides) and one triangle on each vertex.

As the name implies this tiling is constructed by a truncation operation applies to a hexagonal tiling, leaving dodecagons in place of the original hexagons, and new triangles at the original vertex locations. It is given an extended Schläfli symbol of ''t''.

Conway calls it a truncated hextille, constructed as a truncation operation applied to a hexagonal tiling (hextille).

There are 3 regular and 8 semiregular tilings in the plane.

Uniform colorings

There is only one uniform coloring of a truncated hexagonal tiling. (Naming the colors by indices around a vertex: 122.)

Topologically identical tilings

The dodecagonal faces can be distorted into different geometries, such as:

Related polyhedra and tilings

Wythoff constructions from hexagonal and triangular tilings

Like the uniform polyhedra there are eight uniform tilings that can be based from the regular hexagonal tiling (or the dual triangular tiling).

Drawing the tiles colored as red on the original faces, yellow at the original vertices, and blue along the original edges, there are 8 forms, 7 which are topologically distinct. (The ''truncated triangular tiling'' is topologically identical to the hexagonal tiling.)

Symmetry mutations

This tiling is topologically related as a part of sequence of uniform truncated polyhedra with vertex configurations (3.2n.2n), and ,3 Coxeter group symmetry.

Related 2-uniform tilings

Two 2-uniform tilings are related by dissected the dodecagons into a central hexagonal and 6 surrounding triangles and squares.

Circle packing

The truncated hexagonal tiling can be used as a circle packing, placing equal diameter circles at the center of every point.Order in Space: A design source book, Keith Critchlow, p.74-75, pattern G Every circle is in contact with 3 other circles in the packing ( kissing number). This is the lowest density packing that can be created from a uniform tiling.
:

Triakis triangular tiling

The triakis triangular tiling is a tiling of the Euclidean plane. It is an equilateral triangular tiling with each triangle divided into three obtuse triangles (angles 30-30-120) from the center point. It is labeled by face configuration V3.12.12 because each isosceles triangle face has two types of vertices: one with 3 triangles, and two with 12 triangles.

Conway calls it a kisdeltille, constructed as a kis operation applied to a triangular tiling (deltille).

In Japan the pattern is called asanoha for ''hemp leaf'', although the name also applies to other triakis shapes like the triakis icosahedron and triakis octahedron.

It is the dual tessellation of the truncated hexagonal tiling which has one triangle and two dodecagons at each vertex.
:

It is one of eight edge tessellations, tessellations generated by reflections across each edge of a prototile..

Related duals to uniform tilings

It is one of 7 dual uniform tilings in hexagonal symmetry, including the regular duals.

See also

* Tilings of regular polygons
* List of uniform tilings

References

* John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, ''The Symmetries of Things'' 2008,

* (Chapter 2.1: ''Regular and uniform tilings'', p. 58-65)
*
* Keith Critchlow, ''Order in Space: A design source book'', 1970, p. 69-61, Pattern E, Dual p. 77-76, pattern 1
* Dale Seymour and Jill Britton, ''Introduction to Tessellations'', 1989, , pp. 50–56, dual p. 117

External links

*
*

{{Tessellation

Euclidean tilings
Hexagonal tilings
Isogonal tilings
Semiregular tilings
Truncated tilings