Tricorn (mathematics)

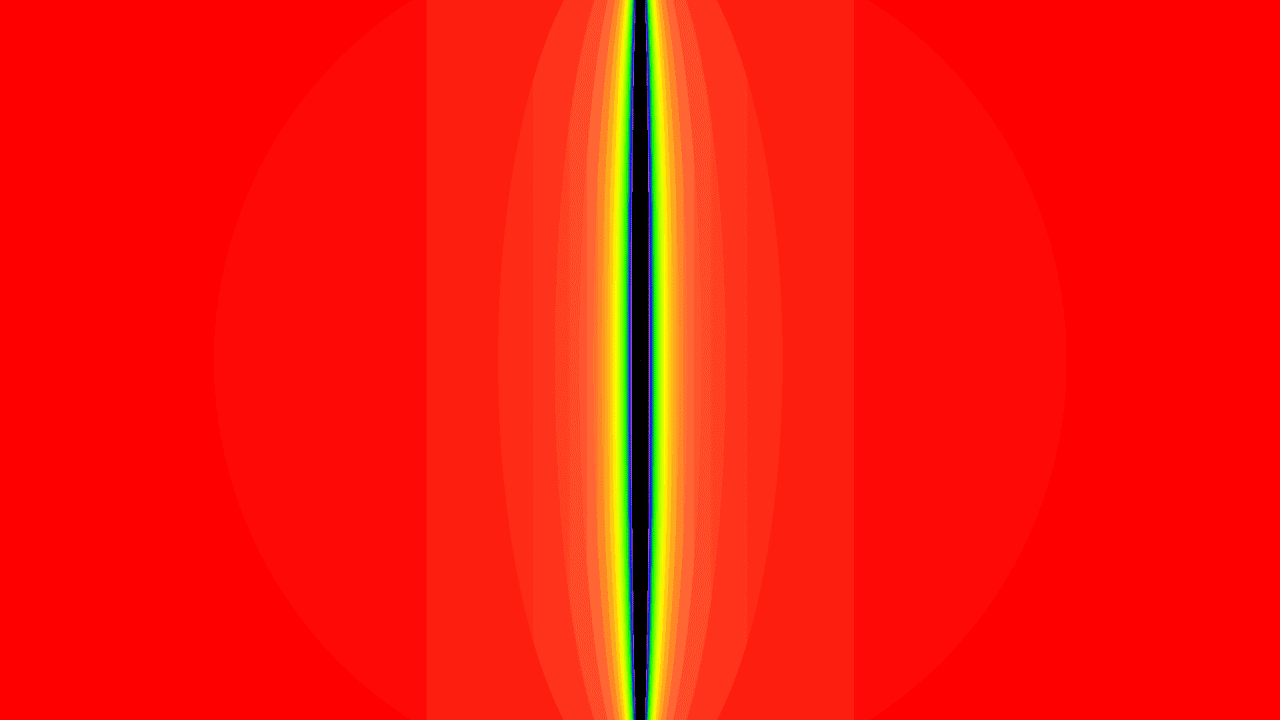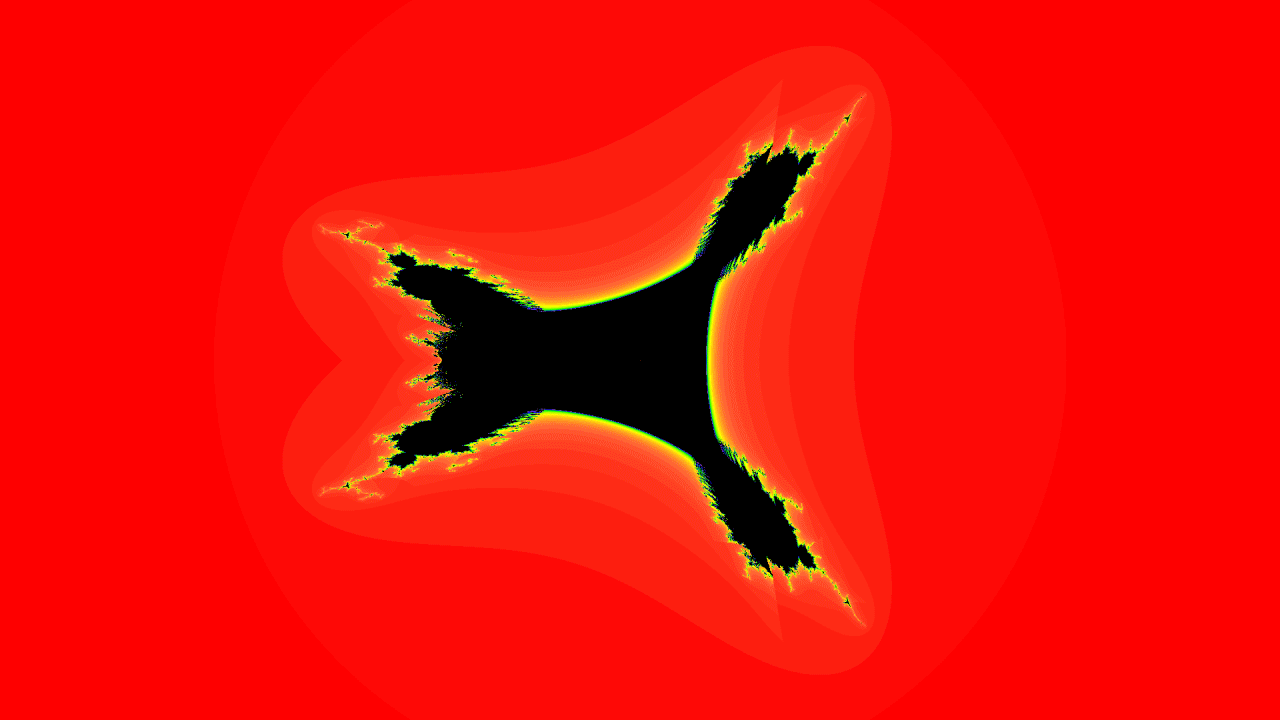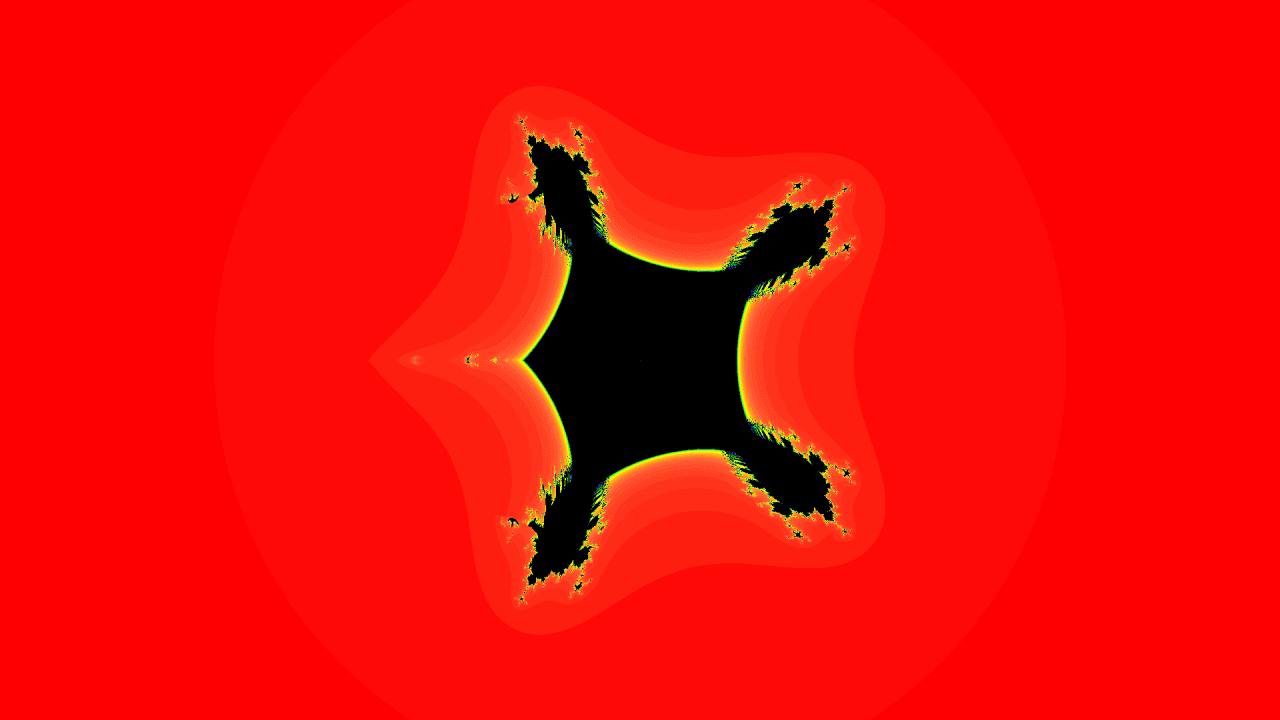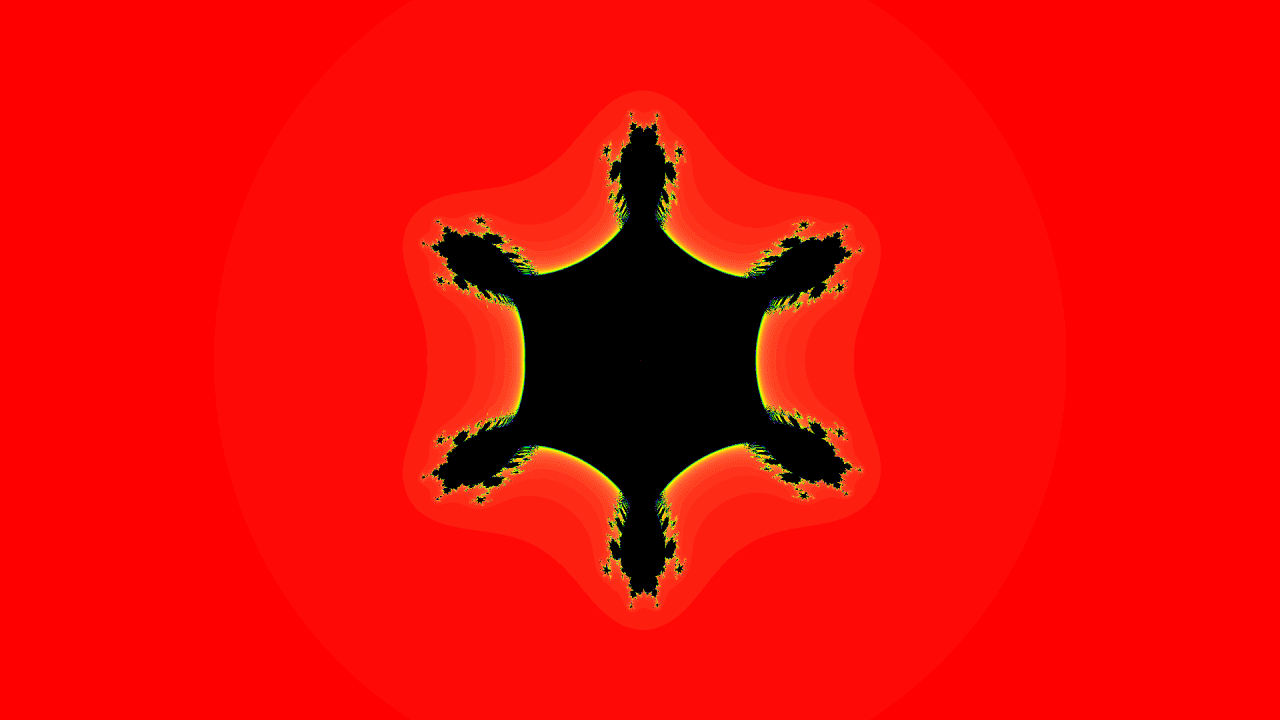In mathematics, the tricorn, sometimes called the Mandelbar set, is a fractal defined in a similar way to the Mandelbrot set, but using the mapping $z \mapsto \bar^2 + c$ instead of $z \mapsto z^2 + c$ used for the Mandelbrot set. It was introduced by W. D. Crowe, R. Hasson, P. J. Rippon, and P. E. D. Strain-Clark. John Milnor found tricorn-like sets as a prototypical configuration in the parameter space of real cubic polynomials, and in various other families of rational maps.

The characteristic three-cornered shape created by this fractal repeats with variations at different scales, showing the same sort of self-similarity as the Mandelbrot set. In addition to smaller tricorns, smaller versions of the Mandelbrot set are also contained within the tricorn fractal.

Formal definition

The tricorn $T$ is defined by a family of quadratic antiholomorphic polynomials

:$f_c:\mathbb C\to\mathbb C$

given by

:$f_c: z\mapsto \bar^2 + c,$

where $c$ is a complex parameter. For each $c$, one looks at the forward orbit
:$(0, f_c(0), f_c(f_c(0)), f_c(f_c(f_c(0))), \ldots)$
of the critical point $0$ of the antiholomorphic polynomial $p_c$. In analogy with the Mandelbrot set, the tricorn is defined as the set of all parameters $c$ for which the forward orbit of the critical point is bounded. This is equivalent to saying that the tricorn is the connectedness locus of the family of quadratic antiholomorphic polynomials; i.e. the set of all parameters $c$ for which the Julia set $J(f_c)$ is connected.

The higher degree analogues of the tricorn are known as the multicorns. These are the connectedness loci of the family of antiholomorphic polynomials $f_c: z\mapsto \bar^d + c$.

Basic properties

* The tricorn is compact, and connected. In fact, Nakane modified Douady and Hubbard's proof of the connectedness of the Mandelbrot set to construct a dynamically defined real-analytic diffeomorphism from the exterior of the tricorn onto the exterior of the closed unit disc in the complex plane. One can define external parameter rays of the tricorn as the inverse images of radial lines under this diffeomorphism.
* Every hyperbolic component of the tricorn is simply connected.
* The boundary of every hyperbolic component of odd period of the tricorn contains real-analytic arcs consisting of quasi-conformally equivalent but conformally distinct parabolic parameters. Such an arc is called a parabolic arc of the tricorn. This is in stark contrast with the corresponding situation for the Mandelbrot set, where parabolic parameters of a given period are known to be isolated.
* The boundary of every odd period hyperbolic component consists only of parabolic parameters. More precisely, the boundary of every hyperbolic component of odd period of the tricorn is a simple closed curve consisting of exactly three parabolic cusp points as well as three parabolic arcs, each connecting two parabolic cusps.
* Every parabolic arc of period k has, at both ends, an interval of positive length across which bifurcation from a hyperbolic component of odd period k to a hyperbolic component of period 2k occurs.

Image gallery of various zooms

Much like the Mandelbrot set, the tricorn has many complex and intricate designs. Due to their similarity, they share many features. However, in the tricorn such features appear to be squeezed and stretched along its boundary.

The following images are progressional zooms on a selected $c$ value where $c = 0.48 + 0.58i$. The images are not stretched or altered, that is how they look on magnification.

Tricornx1.png, Starting zoom. The Tricorn as a whole.
Tricornx6.png, 6 times the original zoom. Many "extrusions" or "seahorses" along the upper "head" are being converged onto the "neck". Aptly named "Seahorse convergence valley".
Tricornx20.png, 20 times the original zoom. Closer look at one side of the "valley". The "seahorses" begin to take shape, they look to be distorted from the original "seahorses" along the Mandelbrots boundary.
Tricornx40.png, 40 times the original zoom. The "seahorse" can be fully seen now.

Implementation

The below pseudocode implementation hardcodes the complex operations for Z. Consider implementing complex number operations to allow for more dynamic and reusable code.
For each pixel (x, y) on the screen, do:

Further topological properties

The tricorn is not path connected. Hubbard and Schleicher showed that there are hyperbolic components of odd period of the tricorn that cannot be connected to the hyperbolic component of period one by paths. A stronger statement to the effect that no two (non-real) odd period hyperbolic components of the tricorn can be connected by a path was proved by Inou and Mukherjee.

It is well known that every rational parameter ray of the Mandelbrot set lands at a single parameter. On the other hand, the rational parameter rays at odd-periodic (except period one) angles of the tricorn accumulate on arcs of positive length consisting of parabolic parameters.
Moreover, unlike the Mandelbrot set, the dynamically natural straightening map from a baby tricorn to the original tricorn is discontinuous at infinitely many parameters.

References

{{DEFAULTSORT:Tricorn (Mathematics)
Fractals