Trapezoid Graph

In 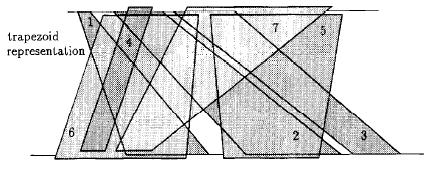graph theory, trapezoid graphs are intersection graphs of trapezoids between two horizontal lines. They are a class of co-comparability graphs that contain interval graphs and permutation graphs as subclasses. A graph is a trapezoid graph if there exists a set of trapezoids corresponding to the vertices of the graph such that two vertices are joined by an edge if and only if the corresponding trapezoids intersect. Trapezoid graphs were introduced by Dagan, Golumbic, and Pinter in 1988. There exists $(n\log n)$ algorithms for chromatic number, weighted independent set, clique cover, and maximum weighted clique.

Definitions and characterizations

Given a channel, a pair of two horizontal lines, a trapezoid between these lines is defined by two points on the top and two points on the bottom line. A graph is a trapezoid graph if there exists a set of trapezoids corresponding to the vertices of the graph such that two vertices are joined by an edge if and only if the corresponding trapezoids intersect.
The interval order dimension of a partially ordered set, $P=(X, <)$, is the minimum number d of interval orders P₁ … P_d such that P = P₁∩…∩P_d. The incomparability graph of a partially ordered set $P=(X, <)$ is the undirected graph $G=(X, E)$ where ''x'' is adjacent to ''y'' in G if and only if ''x'' and ''y'' are incomparable in P. An undirected graph is a trapezoid graph if and only if it is the incomparability graph of a partial order having interval order dimension at most 2.

Applications

The problems of finding maximum cliques and of coloring trapezoid graphs are connected to channel routing problems in VLSI design. Given some labeled terminals on the upper and lower side of a two-sided channel, terminals with the same label will be connected in a common net. This net can be represented by a trapezoid containing the rightmost terminals and leftmost terminals with the same label. Nets may be routed without intersection if and only if the corresponding trapezoids do not intersect. Therefore, the number of layers needed to route the nets without intersection is equal to the graph’s chromatic number.

Equivalent representations

Trapezoid representation

Trapezoids can be used to represent a trapezoid graph by using the definition of trapezoid graph. A trapezoid graph's trapezoid representation can be seen in Figure 1.

Box representation

Dominating rectangles, or box representation, maps the points on the lower of the two lines of the trapezoid representation as lying on the ''x''-axis and that of the upper line as lying on the ''y''-axis of the Euclidean plane. Each trapezoid then corresponds to an axis-parallel box in the plane. Using the notion of a dominance order (In R^''K'', ''x'' is said to be dominated by ''y'', denoted ''x'' < ''y'', if ''x_i'' is less than ''y_i'' for ''i'' = 1, …, ''k''), we say that a box b dominates a box ''b’'' if the lower corner of ''b'' dominates the upper corner of ''b’''. Furthermore, if one of two boxes dominates the other we say that they are comparable. Otherwise, they are incomparable. Thus, two trapezoids are disjoint exactly if their corresponding boxes are comparable. The box representation is useful because the associated dominance order allows sweep line algorithms to be used.

Bitolerance graphs

Bitolerance graphs are incomparability graphs of a bitolerance order. An order is a bitolerance order if and only if there are intervals I_''x'' and real numbers ''t''₁(''x'') and ''t''_''r''(''x'') assigned to each vertex ''x'' in such a way that ''x'' < ''y'' if and only if the overlap of I_''x'' and I_''y'' is less than both ''t''_''r''(''x'') and ''t''₁(''y'') and the center of I_''x'' is less than the center of I_''y''. In 1993, Langley showed that the bounded bitolerance graphs are equivalent to the class of trapezoid graphs.

Relation to other families of graphs

The class of trapezoid graphs properly contains the union of interval and permutation graphs and is equivalent to the incomparability graphs of partially ordered sets having interval order dimension at most two. Permutation graphs can be seen as the special case of trapezoid graphs when every trapezoid has zero area. This occurs when both of the trapezoid’s points on the upper channel are in the same position and both points on the lower channel are in the same position.

Like all incomparability graphs, trapezoid graphs are perfect.

Circle trapezoid graphs

Circle trapezoid graphs are a class of graphs proposed by Felsner et al. in 1993. They are a superclass of the trapezoid graph class, and also contain circle graphs and circular-arc graphs. A circle trapezoid is the region in a circle that lies between two non-crossing chords and a circle trapezoid graph is the intersection graph of families of circle trapezoids on a common circle. There is an $O(n^2)$ algorithm for maximum weighted independent set problem and an $(n^2 \log n)$ algorithm for the maximum weighted clique problem.

''k''-Trapezoid graphs

''k''-Trapezoid graphs are an extension of trapezoid graphs to higher dimension orders. They were first proposed by Felsner, and they rely on the definition of dominating boxes carrying over to higher dimensions in which a point ''x'' is represented by a vector $( x_1, \ldots , x_k )$. Using (''k'' − 1)-dimensional range trees to store and query coordinates, Felsner’s algorithms for chromatic number, maximum clique, and maximum independent set can be applied to ''k''-trapezoid graphs in $(n \log^n)$ time.

Algorithms

Algorithms for trapezoid graphs should be compared with algorithms for general co-comparability graphs. For this larger class of graphs, the maximum independent set and the minimum clique cover problem can be solved in $(n^2\log n)$ time.
Dagan et al. first proposed an $(nk)$ algorithm for coloring trapezoid graphs, where n is the number of nodes and k is the chromatic number of the graph.
Later, using the box representation of trapezoid graphs, Felsner published $(n\log n)$ algorithms for chromatic number, weighted independent set, clique cover, and maximum weighted clique. These algorithms all require $(n)$ space. These algorithms rely on the associated dominance in the box representation that allows sweeping line algorithms to be used. Felsner proposes using balanced trees that can do insert, delete, and query operations in $(\log n)$ time, which results in $(n\log n)$ algorithms.

Recognition

To determine if a graph $$ is a trapezoid graph, search for a transitive orientation $$ on the complement of $$. Since trapezoid graphs are a subset of co-comparability graphs, if $$ is a trapezoid graph, its complement $$ must be a comparability graph. If a transitive orientation $$ of the complement $$ does not exist, $$ is not a trapezoid graph. If $$ does exist, test to see if the order given by $$ is a trapezoid order. The fastest algorithm for trapezoid order recognition was proposed by McConnell and Spinrad in 1994, with a running time of $O(n^2)$. The process reduces the interval dimension 2 question to a problem of covering an associated bipartite graph by chain graphs (graphs with no induced 2K₂).
Using vertex splitting, the recognition problem for trapezoid graphs was shown by Mertzios and Corneil to succeed in $O(n(n+m))$ time, where $m$ denotes the number of edges. This process involves augmenting a given graph $$, and then transforming the augmented graph by replacing each of the original graph’s vertices by a pair of new vertices. This “split graph” is a permutation graph with special properties if an only if $$ is a trapezoid graph.G. B. Mertzios and D. G. Corneil. Vertex splitting and the recognition of trapezoid graphs. Discrete Applied Mathematics, 159(11), pages 1131-1147, 2011.

Notes

References

* {{Cite book
, author = Golumbic, Martin Charles
, authorlink = Martin Charles Golumbic
, title = Algorithmic Graph Theory and Perfect Graphs
, publisher = Academic Press
, year = 1980
, isbn = 0-444-51530-5
, url = http://www.elsevier.com/wps/find/bookdescription.cws_home/699916/description#description
Second edition, Annals of Discrete Mathematics 57, Elsevier, 2004.

Intersection classes of graphs
Perfect graphs