Topological insulator on:
[Wikipedia]
[Google]
[Amazon]
 A topological insulator is a material whose interior behaves as an
A topological insulator is a material whose interior behaves as an
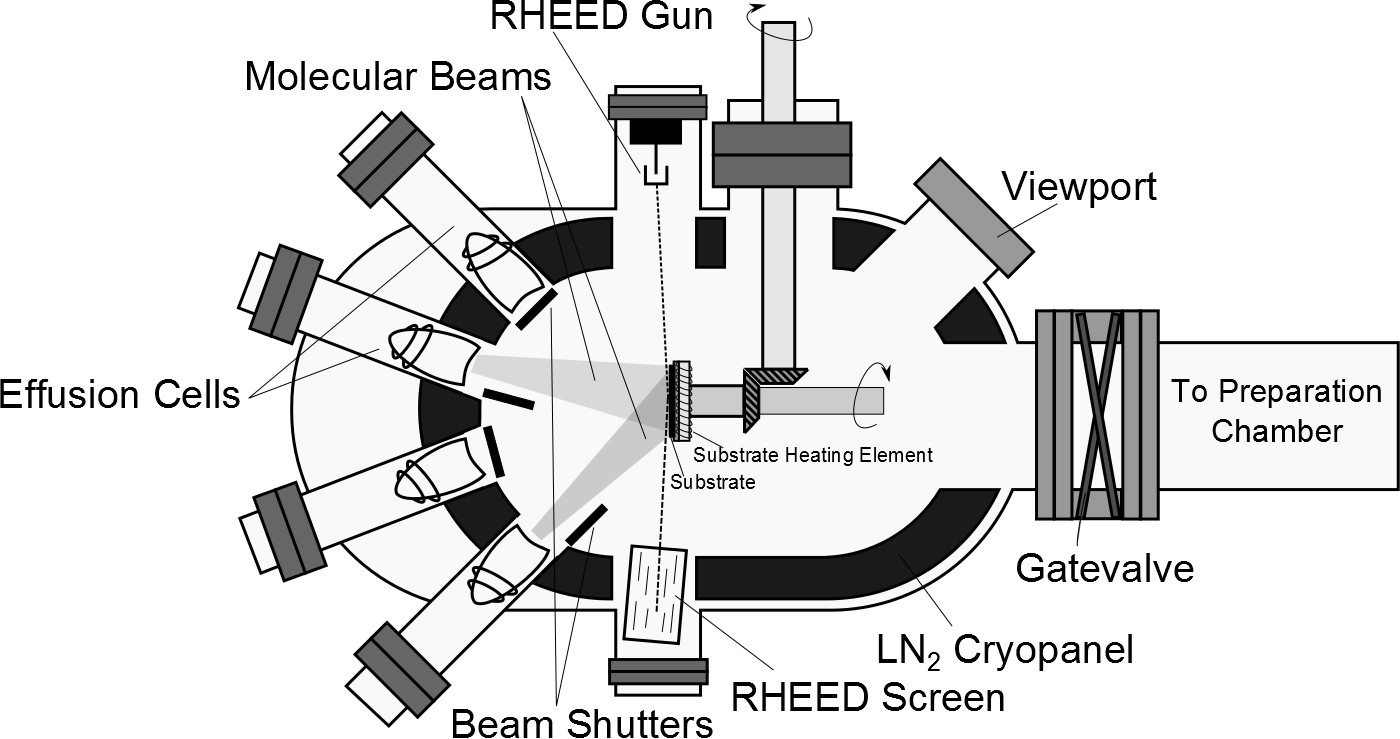 (MBE). MBE has so far been the most common experimental technique. The growth of thin film topological insulators is governed by weak van der Waals interactions. The weak interaction allows to exfoliate the thin film from bulk crystal with a clean and perfect surface. The van der Waals interactions in epitaxy also known as van der Waals epitaxy (VDWE), is a phenomenon governed by weak van der Waals interactions between layered materials of different or same elements in which the materials are stacked on top of each other. This approach allows the growth of layered topological insulators on other substrates for
(MBE). MBE has so far been the most common experimental technique. The growth of thin film topological insulators is governed by weak van der Waals interactions. The weak interaction allows to exfoliate the thin film from bulk crystal with a clean and perfect surface. The van der Waals interactions in epitaxy also known as van der Waals epitaxy (VDWE), is a phenomenon governed by weak van der Waals interactions between layered materials of different or same elements in which the materials are stacked on top of each other. This approach allows the growth of layered topological insulators on other substrates for
electrical insulator
An electrical insulator is a material in which electric current does not flow freely. The atoms of the insulator have tightly bound electrons which cannot readily move. Other materials—semiconductors and electrical conductor, conductors—con ...
while its surface behaves as an electrical conductor
In physics and electrical engineering, a conductor is an object or type of material that allows the flow of charge (electric current) in one or more directions. Materials made of metal are common electrical conductors. The flow of negatively c ...
, meaning that electrons can only move along the surface of the material.
A topological insulator is an insulator for the same reason a " trivial" (ordinary) insulator is: there exists an energy gap between the valence and conduction bands
In solid-state physics, the valence band and conduction band are the bands closest to the Fermi level, and thus determine the electrical conductivity of the solid. In nonmetals, the valence band is the highest range of electron energies in ...
of the material. But in a topological insulator, these bands are, in an informal sense, "twisted", relative to a trivial insulator. The topological insulator cannot be continuously transformed into a trivial one without untwisting the bands, which closes the band gap and creates a conducting state. Thus, due to the continuity of the underlying field, the border
Borders are generally defined as geography, geographical boundaries, imposed either by features such as oceans and terrain, or by polity, political entities such as governments, sovereign states, federated states, and other administrative divisio ...
of a topological insulator with a trivial insulator (including vacuum
A vacuum (: vacuums or vacua) is space devoid of matter. The word is derived from the Latin adjective (neuter ) meaning "vacant" or "void". An approximation to such vacuum is a region with a gaseous pressure much less than atmospheric pressur ...
, which is topologically trivial) is forced to support conducting edge states.
Since this results from a global property of the topological insulator's band structure, local (symmetry-preserving) perturbations cannot damage this surface state. This is unique to topological insulators: while ordinary insulators can also support conductive surface states, only the surface states of topological insulators have this robustness property.
This leads to a more formal definition of a topological insulator: an insulator which cannot be adiabatically
Adiabatic (from ''Gr.'' ἀ ''negative'' + διάβασις ''passage; transference'') refers to any process that occurs without heat transfer. This concept is used in many areas of physics and engineering. Notable examples are listed below.
A ...
transformed into an ordinary insulator without passing through an intermediate conducting state. In other words, topological insulators and trivial insulators are separate regions in the phase diagram, connected only by conducting phases. In this way, topological insulators provide an example of a state of matter
In physics, a state of matter is one of the distinct forms in which matter can exist. Four states of matter are observable in everyday life: solid, liquid, gas, and Plasma (physics), plasma.
Different states are distinguished by the ways the ...
not described by the Landau symmetry-breaking theory that defines ordinary states of matter.
The properties of topological insulators and their surface states are highly dependent on both the dimension of the material and its underlying symmetries
Symmetry () in everyday life refers to a sense of harmonious and beautiful proportion and balance. In mathematics, the term has a more precise definition and is usually used to refer to an object that is invariant under some transformations ...
, and can be classified using the so-called periodic table of topological insulators. Some combinations of dimension and symmetries forbid topological insulators completely. All topological insulators have at least U(1) symmetry from particle number conservation, and often have time-reversal symmetry
T-symmetry or time reversal symmetry is the theoretical symmetry (physics), symmetry of physical laws under the Transformation (mathematics), transformation of time reversal,
: T: t \mapsto -t.
Since the second law of thermodynamics states that ...
from the absence of a magnetic field. In this way, topological insulators are an example of symmetry-protected topological order
Symmetry-protected topological (SPT) order is a kind of order in absolute zero, zero-temperature quantum-mechanical states of matter that have a symmetry and a finite energy gap.
To derive the results in a most-invariant way, renormalization gro ...
. So-called "topological invariants", taking values in or , allow classification of insulators as trivial or topological, and can be computed by various methods.
The surface states of topological insulators can have exotic properties. For example, in time-reversal symmetric 3D topological insulators, surface states have their spin locked at a right-angle to their momentum (spin-momentum locking). At a given energy the only other available electronic states have different spin, so "U"-turn scattering is strongly suppressed and conduction on the surface is highly metallic.
Despite their origin in quantum mechanical systems, analogues of topological insulators can also be found in classical media. There exist photonic, magnetic
Magnetism is the class of physical attributes that occur through a magnetic field, which allows objects to attract or repel each other. Because both electric currents and magnetic moments of elementary particles give rise to a magnetic field, m ...
, and acoustic topological insulators, among others.
Prediction
The first models of 3D topological insulators were proposed by B. A. Volkov and O. A. Pankratov in 1985, and subsequently by Pankratov, S. V. Pakhomov, and Volkov in 1987. Gapless 2D Dirac states were shown to exist at the band inversion contact in PbTe/ SnTe and HgTe/ CdTe heterostructures. Existence of interface Dirac states in HgTe/CdTe was experimentally verified by Laurens W. Molenkamp's group in 2D topological insulators in 2007. Later sets of theoretical models for the 2D topological insulator (also known as the quantum spin Hall insulators) were proposed by Charles L. Kane and Eugene J. Mele in 2005, and also by B. Andrei Bernevig and Shoucheng Zhang in 2006. The topological invariant was constructed and the importance of the time reversal symmetry was clarified in the work by Kane and Mele. Subsequently, Bernevig, Taylor L. Hughes and Zhang made a theoretical prediction that 2D topological insulator with one-dimensional (1D) helical edge states would be realized in quantum wells (very thin layers) of mercury telluride sandwiched between cadmium telluride. The transport due to 1D helical edge states was indeed observed in the experiments by Molenkamp's group in 2007. Although the topological classification and the importance of time-reversal symmetry was pointed in the 2000s, all the necessary ingredients and physics of topological insulators were already understood in the works from the 1980s. In 2007, it was predicted that 3D topological insulators might be found in binary compounds involvingbismuth
Bismuth is a chemical element; it has symbol Bi and atomic number 83. It is a post-transition metal and one of the pnictogens, with chemical properties resembling its lighter group 15 siblings arsenic and antimony. Elemental bismuth occurs nat ...
, and in particular "strong topological insulators" exist that cannot be reduced to multiple copies of the quantum spin Hall state.
Experimental realization
2D Topological insulators were first realized in system containing HgTe quantum wells sandwiched between cadmium telluride in 2007. The first 3D topological insulator to be realized experimentally was Bi1 − x Sb x. Bismuth in its pure state, is asemimetal
A semimetal is a material with a small energy overlap between the bottom of the Electrical conduction, conduction Electronic band structure, band and the top of the valence band, but they do not overlap in momentum space. According to Band theory ...
with a small electronic band gap. Using angle-resolved photoemission spectroscopy
Angle-resolved photoemission spectroscopy (ARPES) is an experimental technique used in condensed matter physics to probe the allowed energies and momenta of the electrons in a material, usually a crystalline solid. It is based on the photoel ...
, and many other measurements, it was observed that Bi1 − xSbx alloy exhibits an odd surface state (SS) crossing between any pair of Kramers points and the bulk features massive Dirac fermions. Additionally, bulk Bi1 − xSbx has been predicted to have 3D Dirac particles. This prediction is of particular interest due to the observation of charge quantum Hall fractionalization in 2D graphene and pure bismuth.
Shortly thereafter symmetry-protected surface states were also observed in pure antimony
Antimony is a chemical element; it has chemical symbol, symbol Sb () and atomic number 51. A lustrous grey metal or metalloid, it is found in nature mainly as the sulfide mineral stibnite (). Antimony compounds have been known since ancient t ...
, bismuth selenide, bismuth telluride
Bismuth telluride () is a gray powder that is a compound of bismuth and tellurium also known as bismuth(III) telluride. It is a semiconductor, which, when alloyed with antimony or selenium, is an efficient thermoelectric material for refrigeration ...
and antimony telluride using angle-resolved photoemission spectroscopy
Angle-resolved photoemission spectroscopy (ARPES) is an experimental technique used in condensed matter physics to probe the allowed energies and momenta of the electrons in a material, usually a crystalline solid. It is based on the photoel ...
(ARPES). and bismuth selenide. Many semiconductors within the large family of Heusler materials are now believed to exhibit topological surface states. In some of these materials, the Fermi level actually falls in either the conduction or valence bands due to naturally-occurring defects, and must be pushed into the bulk gap by doping or gating. The surface states of a 3D topological insulator is a new type of two-dimensional electron gas
A two-dimensional electron gas (2DEG) is a scientific model in solid-state physics. It is an Fermi gas, electron gas that is free to move in two dimensions, but tightly confined in the third. This tight confinement leads to quantized energy levels ...
(2DEG) where the electron's spin is locked to its linear momentum.
Fully bulk-insulating or intrinsic 3D topological insulator states exist in Bi-based materials as demonstrated in surface transport measurements. In a new Bi based chalcogenide (Bi1.1Sb0.9Te2S) with slightly Sn - doping, exhibits an intrinsic semiconductor behavior with Fermi energy and Dirac point lie in the bulk gap and the surface states were probed by the charge transport experiments.
It was proposed in 2008 and 2009 that topological insulators are best understood not as surface conductors per se, but as bulk 3D magnetoelectrics with a quantized magnetoelectric effect. This can be revealed by placing topological insulators in magnetic field. The effect can be described in language similar to that of the hypothetical axion particle of particle physics. The effect was reported by researchers at Johns Hopkins University
The Johns Hopkins University (often abbreviated as Johns Hopkins, Hopkins, or JHU) is a private university, private research university in Baltimore, Maryland, United States. Founded in 1876 based on the European research institution model, J ...
and Rutgers University
Rutgers University ( ), officially Rutgers, The State University of New Jersey, is a Public university, public land-grant research university consisting of three campuses in New Jersey. Chartered in 1766, Rutgers was originally called Queen's C ...
using THz spectroscopy who showed that the Faraday rotation was quantized by the fine structure constant.
In 2012, topological Kondo insulators were identified in samarium hexaboride, which is a bulk insulator at low temperatures.
In 2014, it was shown that magnetic components, like the ones in spin-torque computer memory, can be manipulated by topological insulators. The effect is related to metal–insulator transition
Metal–insulator transitions are transitions of a material from a metal (material with good electrical conductivity of electric charges) to an insulator (material where conductivity of charges is quickly suppressed). These transitions can be ac ...
s (Bose–Hubbard model
The Bose–Hubbard model gives a description of the physics of interacting spinless bosons on a Lattice model (physics), lattice. It is closely related to the Hubbard model that originated in solid-state physics as an approximate description of sup ...
).
Floquet topological insulators
Topological insulators are challenging to synthesize, and limited in topological phases accessible with solid-state materials. This has motivated the search for topological phases on the systems that simulate the same principles underlying topological insulators. Discrete time quantum walks (DTQW) have been proposed for making Floquet topological insulators (FTI). This periodically driven system simulates an effective ( Floquet) Hamiltonian that is topologically nontrivial. This system replicates the effective Hamiltonians from all universal classes of 1- to 3-D topological insulators. Interestingly, topological properties of Floquet topological insulators could be controlled via an external periodic drive rather than an external magnetic field. An atomic lattice empowered by distance selective Rydberg interaction could simulate different classes of FTI over a couple of hundred sites and steps in 1, 2 or 3 dimensions. The long-range interaction allows designing topologically ordered periodic boundary conditions, further enriching the realizable topological phases.Properties and applications
Spin-momentum locking in the topological insulator allows symmetry-protected surface states to hostMajorana particle
In particle physics a Majorana fermion (, uploaded 19 April 2013, retrieved 5 October 2014; and also based on Ettore Majorana, the pronunciation of physicist's name.) or Majorana particle is a fermion that is its own antiparticle. They were hyp ...
s if superconductivity is induced on the surface of 3D topological insulators via proximity effects. (Note that Majorana zero-mode can also appear without topological insulators.) The non-trivialness of topological insulators is encoded in the existence of a gas of helical Dirac fermions. Dirac particles which behave like massless relativistic fermions have been observed in 3D topological insulators. Note that the gapless surface states of topological insulators differ from those in the quantum Hall effect
The quantum Hall effect (or integer quantum Hall effect) is a quantized version of the Hall effect which is observed in two-dimensional electron systems subjected to low temperatures and strong magnetic fields, in which the Hall resistance exhi ...
: the gapless surface states of topological insulators are symmetry-protected (i.e., not topological), while the gapless surface states in quantum Hall effect are topological (i.e., robust against any local perturbations that can break all the symmetries). The topological invariants cannot be measured using traditional transport methods, such as spin Hall conductance, and the transport is not quantized by the invariants. An experimental method to measure topological invariants was demonstrated which provide a measure of the topological order. (Note that the term topological order has also been used to describe the topological order
In physics, topological order describes a state or phase of matter that arises system with non-local interactions, such as entanglement in quantum mechanics, and floppy modes in elastic systems. Whereas classical phases of matter such as gases an ...
with emergent gauge theory
In physics, a gauge theory is a type of field theory in which the Lagrangian, and hence the dynamics of the system itself, does not change under local transformations according to certain smooth families of operations (Lie groups). Formally, t ...
discovered in 1991.) More generally (in what is known as the ''ten-fold way'') for each spatial dimensionality, each of the ten Altland—Zirnbauer symmetry classes of random Hamiltonians labelled by the type of discrete symmetry (time-reversal symmetry, particle-hole symmetry, and chiral symmetry) has a corresponding group of topological invariants (either , or trivial) as described by the periodic table of topological invariants The periodic table of topological insulators and topological superconductors, also called tenfold classification of topological insulators and superconductors, is an application of topology to condensed matter physics. It indicates the mathematical ...
.
The most promising applications of topological insulators are spintronic devices and dissipationless transistor
A transistor is a semiconductor device used to Electronic amplifier, amplify or electronic switch, switch electrical signals and electric power, power. It is one of the basic building blocks of modern electronics. It is composed of semicondu ...
s for quantum computer
A quantum computer is a computer that exploits quantum mechanical phenomena. On small scales, physical matter exhibits properties of both particles and waves, and quantum computing takes advantage of this behavior using specialized hardware. ...
s based on the quantum Hall effect
The quantum Hall effect (or integer quantum Hall effect) is a quantized version of the Hall effect which is observed in two-dimensional electron systems subjected to low temperatures and strong magnetic fields, in which the Hall resistance exhi ...
and quantum anomalous Hall effect. In addition, topological insulator materials have also found practical applications in advanced magnetoelectronic and optoelectronic
Optoelectronics (or optronics) is the study and application of electronic devices and systems that find, detect and control light, usually considered a sub-field of photonics. In this context, ''light'' often includes invisible forms of radia ...
devices.
Thermoelectrics
Some of the most well-known topological insulators are also thermoelectric materials, such as Bi2Te3 and its alloys with Bi2Se3 (n-type thermoelectrics) and Sb2Te3 (p-type thermoelectrics). High thermoelectric power conversion efficiency is realized in materials with low thermal conductivity, high electrical conductivity, and highSeebeck coefficient
The Seebeck coefficient (also known as thermopower, thermoelectric power, and thermoelectric sensitivity) of a material is a measure of the magnitude of an induced thermoelectric voltage in response to a temperature difference across that material ...
(i.e., the incremental change in voltage due to an incremental change in temperature). Topological insulators are often composed of heavy atoms, which tends to lower thermal conductivity and are therefore beneficial for thermoelectrics. A recent study also showed that good electrical characteristics (i.e., high electrical conductivity and Seebeck coefficient) can arise in topological insulators due to warping of the bulk band structure, which is driven by band inversion. Often, the electrical conductivity and Seebeck coefficient are conflicting properties of thermoelectrics and difficult to optimize simultaneously. Band warping, induced by band inversion in a topological insulator, can mediate the two properties by reducing the effective mass of electrons/holes and increasing the valley degeneracy (i.e., the number of electronic bands that are contributing to charge transport). As a result, topological insulators are generally interesting candidates for thermoelectric applications.
Synthesis
Topological insulators can be grown using different methods such as metal-organic chemical vapor deposition (MOCVD),physical vapor deposition
Physical vapor deposition (PVD), sometimes called physical vapor transport (PVT), describes a variety of vacuum deposition methods which can be used to produce thin films and coatings on substrates including metals, ceramics, glass, and polym ...
(PVD), solvothermal synthesis, sonochemical technique and molecular beam epitaxy
Molecular-beam epitaxy (MBE) is an epitaxy method for thin-film deposition of single crystals. MBE is widely used in the manufacture of semiconductor devices, including transistors. MBE is used to make diodes and MOSFETs (MOS field-effect transis ...
 (MBE). MBE has so far been the most common experimental technique. The growth of thin film topological insulators is governed by weak van der Waals interactions. The weak interaction allows to exfoliate the thin film from bulk crystal with a clean and perfect surface. The van der Waals interactions in epitaxy also known as van der Waals epitaxy (VDWE), is a phenomenon governed by weak van der Waals interactions between layered materials of different or same elements in which the materials are stacked on top of each other. This approach allows the growth of layered topological insulators on other substrates for
(MBE). MBE has so far been the most common experimental technique. The growth of thin film topological insulators is governed by weak van der Waals interactions. The weak interaction allows to exfoliate the thin film from bulk crystal with a clean and perfect surface. The van der Waals interactions in epitaxy also known as van der Waals epitaxy (VDWE), is a phenomenon governed by weak van der Waals interactions between layered materials of different or same elements in which the materials are stacked on top of each other. This approach allows the growth of layered topological insulators on other substrates for heterostructure
A heterojunction is an interface between two layers or regions of dissimilar semiconductors. These semiconducting materials have unequal band gaps as opposed to a homojunction. It is often advantageous to engineer the electronic energy bands in m ...
and integrated circuit
An integrated circuit (IC), also known as a microchip or simply chip, is a set of electronic circuits, consisting of various electronic components (such as transistors, resistors, and capacitors) and their interconnections. These components a ...
s.
MBE growth of topological insulators
Molecular beam epitaxy (MBE) is an epitaxy
Epitaxy (prefix ''epi-'' means "on top of”) is a type of crystal growth or material deposition in which new crystalline layers are formed with one or more well-defined orientations with respect to the crystalline seed layer. The deposited cry ...
method for the growth of a crystalline material on a crystalline substrate to form an ordered layer. MBE is performed in high vacuum or ultra-high vacuum
Ultra-high vacuum (often spelled ultrahigh in American English, UHV) is the vacuum regime characterised by pressures lower than about . UHV conditions are created by pumping the gas out of a UHV chamber. At these low pressures the mean free path of ...
, the elements are heated in different electron beam evaporators until they sublime. The gaseous elements then condense on the wafer where they react with each other to form single crystal
In materials science, a single crystal (or single-crystal solid or monocrystalline solid) is a material in which the crystal lattice of the entire sample is continuous and unbroken to the edges of the sample, with no Grain boundary, grain bound ...
s.
MBE is an appropriate technique for the growth of high quality single-crystal films. In order to avoid a huge lattice mismatch and defects at the interface, the substrate and thin film are expected to have similar lattice constants. MBE has an advantage over other methods due to the fact that the synthesis is performed in high vacuum hence resulting in less contamination. Additionally, lattice defect is reduced due to the ability to influence the growth rate and the ratio of species of source materials present at the substrate interface. Furthermore, in MBE, samples can be grown layer by layer which results in flat surfaces with smooth interface for engineered heterostructures. Moreover, MBE synthesis technique benefits from the ease of moving a topological insulator sample from the growth chamber to a characterization chamber such as angle-resolved photoemission spectroscopy (ARPES) or scanning tunneling microscopy
A scanning tunneling microscope (STM) is a type of scanning probe microscope used for imaging surfaces at the atomic level. Its development in 1981 earned its inventors, Gerd Binnig and Heinrich Rohrer, then at IBM Zürich, the Nobel Prize in ...
(STM) studies.
Due to the weak van der Waals bonding, which relaxes the lattice-matching condition, TI can be grown on a wide variety of substrates such as Si(111), , GaAs
Gallium arsenide (GaAs) is a III-V direct band gap semiconductor with a zinc blende crystal structure.
Gallium arsenide is used in the manufacture of devices such as microwave frequency integrated circuits, monolithic microwave integrated circui ...
(111),
InP(111), CdS
CDS, CDs, Cds, etc. may refer to:
Finance
* Canadian Depository for Securities, Canadian post-trade financial services company
* Certificate of deposit (CDs)
* Counterfeit Deterrence System, developed by the Central Bank Counterfeit Deterrence ...
(0001) and .
PVD growth of topological insulators
The physical vapor deposition (PVD) technique does not suffer from the disadvantages of the exfoliation method and, at the same time, it is much simpler and cheaper than the fully controlled growth by molecular-beam epitaxy. The PVD method enables a reproducible synthesis of single crystals of various layered quasi-two-dimensional materials including topological insulators (i.e., , ). The resulted single crystals have a well-defined crystallographic orientation; their composition, thickness, size, and the surface density on the desired substrate can be controlled. The thickness control is particularly important for 3D TIs in which the trivial (bulky) electronic channels usually dominate the transport properties and mask the response of the topological (surface) modes. By reducing the thickness, one lowers the contribution of trivial bulk channels into the total conduction, thus forcing the topological modes to carry the electric current.Bismuth-based topological insulators
Thus far, the field of topological insulators has been focused on bismuth and antimonychalcogenide
: 220px, Cadmium sulfide, a prototypical metal chalcogenide, is used as a yellow pigment.
A chalcogenide is a chemical compound consisting of at least one chalcogen anion and at least one more electropositive element. Although all group 16 elemen ...
based materials such as , , or Bi1 − xSbx, Bi1.1Sb0.9Te2S. The choice of chalcogenides is related to the van der Waals relaxation of the lattice matching strength which restricts the number of materials and substrates. Bismuth chalcogenides have been studied extensively for TIs and their applications in thermoelectric materials. The van der Waals interaction in TIs exhibit important features due to low surface energy. For instance, the surface of is usually terminated by Te due to its low surface energy.
Bismuth chalcogenides have been successfully grown on different substrates. In particular, Si has been a good substrate for the successful growth of . However, the use of sapphire as substrate has not been so encouraging due to a large mismatch of about 15%. The selection of appropriate substrate can improve the overall properties of TI. The use of buffer layer can reduce the lattice match hence improving the electrical properties of TI. can be grown on top of various Bi2 − xInxSe3 buffers. Table 1 shows , , on different substrates and the resulting lattice mismatch. Generally, regardless of the substrate used, the resulting films have a textured surface that is characterized by pyramidal single-crystal domains with quintuple-layer steps. The size and relative proportion of these pyramidal domains vary with factors that include film thickness, lattice mismatch with the substrate and interfacial chemistry-dependent film nucleation. The synthesis of thin films have the stoichiometry problem due to the high vapor pressures of the elements. Thus, binary tetradymites are extrinsically doped as n-type (, ) or p-type ( ). Due to the weak van der Waals bonding, graphene is one of the preferred substrates for TI growth despite the large lattice mismatch.
Identification
The first step of topological insulators identification takes place right after synthesis, meaning without breaking the vacuum and moving the sample to an atmosphere. That could be done by using angle-resolved photoemission spectroscopy (ARPES) or scanning tunneling microscopy (STM) techniques. Further measurements includes structural and chemical probes such as X-ray diffraction and energy-dispersive spectroscopy but depending on the sample quality, the lack of sensitivity could remain. Transport measurements cannot uniquely pinpoint the topology by definition of the state.Classification
Bloch's theorem
In condensed matter physics, Bloch's theorem states that solutions to the Schrödinger equation in a periodic potential can be expressed as plane waves modulated by periodic functions. The theorem is named after the Swiss physicist Felix Bloch, ...
allows a full characterization of the wave propagation properties of a material by assigning a matrix to each wave vector in the Brillouin zone
In mathematics and solid state physics, the first Brillouin zone (named after Léon Brillouin) is a uniquely defined primitive cell in reciprocal space
Reciprocal lattice is a concept associated with solids with translational symmetry whic ...
.
Mathematically, this assignment creates a vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X (for example X could be a topological space, a manifold, or an algebraic variety): to eve ...
. Different materials will have different wave propagation properties, and thus different vector bundles. If we consider all insulators (materials with a band gap), this creates a space of vector bundles. It is the topology of this space (modulo trivial bands) from which the "topology" in topological insulators arises.
Specifically, the number of connected components of the space indicates how many different "islands" of insulators exist amongst the metallic states. Insulators in the connected component containing the vacuum state are identified as "trivial", and all other insulators as "topological". The connected component in which an insulator lies can be identified with a number, referred to as a "topological invariant".
This space can be restricted under the presence of symmetries, changing the resulting topology. Although unitary
Unitary may refer to:
Mathematics
* Unitary divisor
* Unitary element
* Unitary group
* Unitary matrix
* Unitary morphism
* Unitary operator
* Unitary transformation
* Unitary representation
* Unitarity (physics)
* ''E''-unitary inverse semigr ...
symmetries are usually significant in quantum mechanics, they have no effect on the topology here. Instead, the three symmetries typically considered are time-reversal symmetry, particle-hole symmetry, and chiral symmetry (also called sublattice symmetry). Mathematically, these are represented as, respectively: an anti-unitary operator which commutes with the Hamiltonian
Hamiltonian may refer to:
* Hamiltonian mechanics, a function that represents the total energy of a system
* Hamiltonian (quantum mechanics), an operator corresponding to the total energy of that system
** Dyall Hamiltonian, a modified Hamiltonian ...
; an anti-unitary operator which anti-commutes with the Hamiltonian; and a unitary operator which anti-commutes with the Hamiltonian. All combinations of the three together with each spatial dimension result in the so-called periodic table of topological insulators.
Future developments
The field of topological insulators still needs to be developed. The best bismuth chalcogenide topological insulators have about 10 meV bandgap variation due to the charge. Further development should focus on the examination of both: the presence of high-symmetry electronic bands and simply synthesized materials. One of the candidates is half-Heusler compounds. These crystal structures can consist of a large number of elements. Band structures and energy gaps are very sensitive to the valence configuration; because of the increased likelihood of intersite exchange and disorder, they are also very sensitive to specific crystalline configurations. A nontrivial band structure that exhibits band ordering analogous to that of the known 2D and 3D TI materials was predicted in a variety of 18-electron half-Heusler compounds using first-principles calculations. These materials have not yet shown any sign of intrinsic topological insulator behavior in actual experiments.See also
*Topological order
In physics, topological order describes a state or phase of matter that arises system with non-local interactions, such as entanglement in quantum mechanics, and floppy modes in elastic systems. Whereas classical phases of matter such as gases an ...
* Topological quantum computer
A topological quantum computer is a type of quantum computer. It utilizes anyons, a type of quasiparticle that occurs in two-dimensional systems. The anyons' world lines intertwine to form braids in a three-dimensional spacetime (one temporal ...
* Topological quantum field theory
In gauge theory and mathematical physics, a topological quantum field theory (or topological field theory or TQFT) is a quantum field theory that computes topological invariants.
While TQFTs were invented by physicists, they are also of mathemati ...
* Topological quantum number
In physics, a topological quantum number (also called topological charge) is any quantity, in a physical theory, that takes on only one of a discrete set of values, due to topological considerations. Most commonly, topological quantum numbers ar ...
* Quantum Hall effect
The quantum Hall effect (or integer quantum Hall effect) is a quantized version of the Hall effect which is observed in two-dimensional electron systems subjected to low temperatures and strong magnetic fields, in which the Hall resistance exhi ...
* Quantum spin Hall effect
The quantum spin Hall state is a state of matter proposed to exist in special, two-dimensional semiconductors that have a quantized spin-Hall conductance and a vanishing charge-Hall conductance. The quantum spin Hall state of matter is the cousin o ...
* Periodic table of topological invariants The periodic table of topological insulators and topological superconductors, also called tenfold classification of topological insulators and superconductors, is an application of topology to condensed matter physics. It indicates the mathematical ...
* Bismuth selenide
* Photonic topological insulator
References
Further reading
* * * * * * * * {{DEFAULTSORT:Topological Insulator Condensed matter physics Semiconductors Topology