Tide Spectrum on:
[Wikipedia]
[Google]
[Amazon]
 The theory of tides is the application of
The theory of tides is the application of
Galileo's Theory of the Tides
by Rossella Gigli, retrieved 10 March 2010 He strongly and mockingly rejects the lunar theory of the tides, and tries to explain the tides as the result of the Earth's rotation and revolution around the Sun, believing that the oceans moved like water in a large basin: as the basin moves, so does the water. Therefore, as the Earth revolves, the force of the Earth's rotation causes the oceans to "alternately accelerate and retardate". His view on the oscillation and "alternately accelerated and retardated" motion of the Earth's rotation is a "dynamic process" that deviated from the previous dogma, which proposed "a process of expansion and contraction of seawater." However, Galileo's theory was erroneous. In subsequent centuries, further analysis led to the current tidal physics. Galileo tried to use his tidal theory to prove the movement of the Earth around the Sun. Galileo theorized that because of the Earth's motion, borders of the oceans like the Atlantic and Pacific would show one high tide and one low tide per day. The Mediterranean Sea had two high tides and low tides, though Galileo argued that this was a product of secondary effects and that his theory would hold in the Atlantic. However, Galileo's contemporaries noted that the Atlantic also had two high tides and low tides per day, which led to Galileo omitting this claim from his 1632 ''Dialogue''. René Descartes theorized that the tides (alongside the movement of planets, etc.) were caused by aetheric vortices, without reference to Kepler's theories of gravitation by mutual attraction; this was extremely influential, with numerous followers of Descartes expounding on this theory throughout the 17th century, particularly in France. However, Descartes and his followers acknowledged the influence of the Moon, speculating that pressure waves from the Moon via the aether were responsible for the correlation.
Satellite observations confirm the accuracy of the dynamic theory, and the tides worldwide are now measured to within a few centimeters. Measurements from the
 Laplace's improvements in theory were substantial, but they still left prediction in an approximate state. This position changed in the 1860s when the local circumstances of tidal phenomena were more fully brought into account by William Thomson's application of
Laplace's improvements in theory were substantial, but they still left prediction in an approximate state. This position changed in the 1860s when the local circumstances of tidal phenomena were more fully brought into account by William Thomson's application of
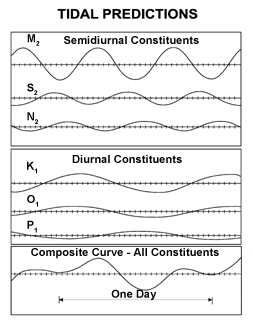 Tidal constituents combine to give an endlessly varying aggregate because of their different and incommensurable frequencies: the effect is visualized in a
Tidal constituents combine to give an endlessly varying aggregate because of their different and incommensurable frequencies: the effect is visualized in a
animation of the American Mathematical Society
illustrating the way in which the components used to be mechanically combined in the tide-predicting machine. Amplitudes (half of
Contributions of satellite laser ranging to the studies of earth tides
** ttp://tidesandcurrents.noaa.gov/publications/Understanding_Tides_by_Steacy_finalFINAL11_30.pdf Understanding Tides*
150 Years of Tides on the Western Coast
*
{{DEFAULTSORT:Theory Of Tides Tides Geophysics Oceanography Continuum mechanics Fluid dynamics Fluid mechanics Planetary science
 The theory of tides is the application of
The theory of tides is the application of continuum mechanics
Continuum mechanics is a branch of mechanics that deals with the mechanical behavior of materials modeled as a continuous mass rather than as discrete particles. The French mathematician Augustin-Louis Cauchy was the first to formulate such m ...
to interpret and predict the tidal deformations of planetary and satellite bodies and their atmospheres and oceans (especially Earth's oceans) under the gravitational loading of another astronomical body or bodies (especially the Moon and Sun).
History
Australian Aboriginal astronomy
The Yolngu people of northeasternArnhem Land
Arnhem Land is a historical region of the Northern Territory of Australia, with the term still in use. It is located in the north-eastern corner of the territory and is around from the territory capital, Darwin. In 1623, Dutch East India Compan ...
in the Northern Territory of Australia identified a link between the Moon and the tides, which they mythically attributed to the Moon filling with water and emptying out again.
Classical era
The tides received relatively little attention in the civilizations around the Mediterranean Sea, as the tides there are relatively small, and the areas that experience tides do so unreliably. A number of theories were advanced, however, from comparing the movements to breathing or blood flow to theories involving whirlpools or river cycles. A similar "breathing earth" idea was considered by some Asian thinkers. Plato reportedly believed that the tides were caused by water flowing in and out of undersea caverns. An ancient Indian Purana text dated to 400-300 BC refers to the ocean rising and falling because ofheat expansion
Thermal expansion is the tendency of matter to change its shape, area, volume, and density in response to a change in temperature, usually not including phase transitions.
Temperature is a monotonic function of the average molecular kinetic ...
from the light of the Moon.
Ultimately the link between the Moon (and Sun) and the tides became known to the Greeks, although the exact date of discovery is unclear; references to it are made in sources such as Pytheas of Massilia in 325 BC and Pliny the Elder's ''Natural History'' in 77 AD. Although the schedule of the tides and the link to lunar and solar movements was known, the exact mechanism that connected them was unclear. Seneca mentions in ''De Providentia
''De Providentia'' (''On Providence'') is a short essay in the form of a dialogue in six brief sections, written by the Latin philosopher Seneca (died AD 65) in the last years of his life. He chose the dialogue form (as in the well-known Plat ...
'' the periodic motion of the tides controlled by the lunar sphere. Eratosthenes
Eratosthenes of Cyrene (; grc-gre, Ἐρατοσθένης ; – ) was a Greek polymath: a mathematician, geographer, poet, astronomer, and music theorist. He was a man of learning, becoming the chief librarian at the Library of Alexandria ...
(3rd century BC) and Posidonius (1st century BC) both produced detailed descriptions of the tides and their relationship to the phases of the Moon, Posidonius in particular making lengthy observations of the sea on the Spanish coast, although little of their work survived. The influence of the Moon on tides was mentioned in Ptolemy's ''Tetrabiblos'' as evidence of the reality of astrology. Seleucus of Seleucia is thought to have theorized around 150 BC that tides were caused by the Moon as part of his heliocentric
Heliocentrism (also known as the Heliocentric model) is the astronomical model in which the Earth and planets revolve around the Sun at the center of the universe. Historically, heliocentrism was opposed to geocentrism, which placed the Earth at ...
model.
Aristotle, judging from discussions of his beliefs in other sources, is thought to have believed the tides were caused by winds driven by the Sun's heat, and he rejected the theory that the Moon caused the tides. An apocryphal legend claims that he committed suicide in frustration with his failure to fully understand the tides. Philostratus discusses tides in Book Five of '' Life of Apollonius of Tyana'' (circa 217-238 AD); he was vaguely aware of a correlation of the tides with the phases of the Moon but attributed them to spirits moving water in and out of caverns, which he connected with the legend that spirits of the dead cannot move on at certain phases of the Moon.
Medieval period
The Venerable Bede discusses the tides in '' The Reckoning of Time'' and shows that the twice-daily timing of tides is related to the Moon and that the lunar monthly cycle of spring and neap tides is also related to the Moon's position. He goes on to note that the times of tides vary along the same coast and that the water movements cause low tide at one place when there is high tide elsewhere. However, he made no progress regarding the question of how exactly the Moon created the tides. Medievalrule-of-thumb
In English language, English, the phrase ''rule of thumb'' refers to an approximate method for doing something, based on practical experience rather than theory. This usage of the phrase can be traced back to the 17th century and has been associat ...
methods for predicting tides were said to allow one "to know what Moon makes high water" from the Moon's movements. Dante references the Moon's influence on the tides in his '' Divine Comedy''.
Medieval European understanding of the tides was often based on works of Muslim astronomers
Islamic astronomy comprises the Astronomy, astronomical developments made in the Islamic world, particularly during the Islamic Golden Age (9th–13th centuries), and mostly written in the Arabic language. These developments mostly took place in ...
, which became available through Latin translation starting from the 12th century. Abu Ma'shar al-Balkhi, in his ''Introductorium in astronomiam'', taught that ebb and flood tides were caused by the Moon. Abu Ma'shar discussed the effects of wind and Moon's phases relative to the Sun on the tides. In the 12th century, al-Bitruji contributed the notion that the tides were caused by the general circulation of the heavens. Medieval Arabic astrologers frequently referenced the Moon's influence on the tides as evidence for the reality of astrology; some of their treatises on the topic influenced western Europe. Some theorized that the influence was caused by lunar rays heating the ocean's floor.
Modern era
Simon Stevin
Simon Stevin (; 1548–1620), sometimes called Stevinus, was a Flemish mathematician, scientist and music theorist. He made various contributions in many areas of science and engineering, both theoretical and practical. He also translated vario ...
in his 1608 ''De spiegheling der Ebbenvloet (The Theory of Ebb and Flood'') dismisses a large number of misconceptions that still existed about ebb and flood. Stevin pleads for the idea that the attraction of the Moon was responsible for the tides and writes in clear terms about ebb, flood, spring tide and neap tide, stressing that further research needed to be made. In 1609, Johannes Kepler
Johannes Kepler (; ; 27 December 1571 – 15 November 1630) was a German astronomer, mathematician, astrologer, natural philosopher and writer on music. He is a key figure in the 17th-century Scientific Revolution, best known for his laws ...
correctly suggested that the gravitation of the Moon causes the tides, which he compared to magnetic
Magnetism is the class of physical attributes that are mediated by a magnetic field, which refers to the capacity to induce attractive and repulsive phenomena in other entities. Electric currents and the magnetic moments of elementary particle ...
attraction basing his argument upon ancient observations and correlations.
In 1616, Galileo Galilei wrote ''Discourse on the Tides
"Discourse on the Tides" ( it, Discorso Sul Flusso E Il Reflusso Del Mare) is an essay written by Galileo Galilei in 1616 as a letter to Alessandro Orsini that attempted to explain the motion of Earth's tides as a consequence of Earth's rotation a ...
.'' Rice UniversityGalileo's Theory of the Tides
by Rossella Gigli, retrieved 10 March 2010 He strongly and mockingly rejects the lunar theory of the tides, and tries to explain the tides as the result of the Earth's rotation and revolution around the Sun, believing that the oceans moved like water in a large basin: as the basin moves, so does the water. Therefore, as the Earth revolves, the force of the Earth's rotation causes the oceans to "alternately accelerate and retardate". His view on the oscillation and "alternately accelerated and retardated" motion of the Earth's rotation is a "dynamic process" that deviated from the previous dogma, which proposed "a process of expansion and contraction of seawater." However, Galileo's theory was erroneous. In subsequent centuries, further analysis led to the current tidal physics. Galileo tried to use his tidal theory to prove the movement of the Earth around the Sun. Galileo theorized that because of the Earth's motion, borders of the oceans like the Atlantic and Pacific would show one high tide and one low tide per day. The Mediterranean Sea had two high tides and low tides, though Galileo argued that this was a product of secondary effects and that his theory would hold in the Atlantic. However, Galileo's contemporaries noted that the Atlantic also had two high tides and low tides per day, which led to Galileo omitting this claim from his 1632 ''Dialogue''. René Descartes theorized that the tides (alongside the movement of planets, etc.) were caused by aetheric vortices, without reference to Kepler's theories of gravitation by mutual attraction; this was extremely influential, with numerous followers of Descartes expounding on this theory throughout the 17th century, particularly in France. However, Descartes and his followers acknowledged the influence of the Moon, speculating that pressure waves from the Moon via the aether were responsible for the correlation.
Newton
Newton most commonly refers to:
* Isaac Newton (1642–1726/1727), English scientist
* Newton (unit), SI unit of force named after Isaac Newton
Newton may also refer to:
Arts and entertainment
* ''Newton'' (film), a 2017 Indian film
* Newton ( ...
, in the '' Principia'', provides a correct explanation for the tidal force, which can be used to explain tides on a planet covered by a uniform ocean but which takes no account of the distribution of the continents or ocean bathymetry.
Dynamic theory
While Newton explained the tides by describing the tide-generating forces andDaniel Bernoulli
Daniel Bernoulli FRS (; – 27 March 1782) was a Swiss mathematician and physicist and was one of the many prominent mathematicians in the Bernoulli family from Basel. He is particularly remembered for his applications of mathematics to mechan ...
gave a description of the static reaction of the waters on Earth to the tidal potential, the ''dynamic theory of tides'', developed by Pierre-Simon Laplace in 1775, describes the ocean's real reaction to tidal forces. Laplace's theory of ocean tides takes into account friction, resonance and natural periods of ocean basins. It predicts the large amphidromic systems in the world's ocean basins and explains the oceanic tides that are actually observed.
The equilibrium theory—based on the gravitational gradient from the Sun and Moon but ignoring the Earth's rotation, the effects of continents, and other important effects—could not explain the real ocean tides. Since measurements have confirmed the dynamic theory, many things have possible explanations now, like how the tides interact with deep sea ridges, and chains of seamounts give rise to deep eddies that transport nutrients from the deep to the surface. The equilibrium tide theory calculates the height of the tide wave of less than half a meter, while the dynamic theory explains why tides are up to 15 meters. Satellite observations confirm the accuracy of the dynamic theory, and the tides worldwide are now measured to within a few centimeters. Measurements from the
CHAMP
Champ is the short form of champion. It may also refer to:
People
* Champ (nickname)
* Champ (surname)
* Champ Butler (1926–1992), American singer
* Champ Lyons (born 1940), justice of the Supreme Court of Alabama from 1998 to 2011
* Champ Se ...
satellite closely match the models based on the TOPEX
TOPEX/Poseidon was a joint satellite altimeter mission between NASA, the U.S. space agency; and CNES, the French space agency, to map ocean surface topography. Launched on August 10, 1992, it was the first major oceanographic research satellite. ...
data. Accurate models of tides worldwide are essential for research since the variations due to tides must be removed from measurements when calculating gravity and changes in sea levels.
Laplace's tidal equations
In 1776, Laplace formulated a single set of linearpartial differential equation
In mathematics, a partial differential equation (PDE) is an equation which imposes relations between the various partial derivatives of a Multivariable calculus, multivariable function.
The function is often thought of as an "unknown" to be sol ...
s for tidal flow described as a barotropic
In fluid dynamics, a barotropic fluid is a fluid whose density is a function of pressure only. The barotropic fluid is a useful model of fluid behavior in a wide variety of scientific fields, from meteorology to astrophysics.
The density of most ...
two-dimensional sheet flow. Coriolis effects
In physics, the Coriolis force is an inertial or fictitious force that acts on objects in motion within a frame of reference that rotates with respect to an inertial frame. In a reference frame with clockwise rotation, the force acts to the ...
are introduced as well as lateral forcing by gravity. Laplace obtained these equations by simplifying the fluid dynamics
In physics and engineering, fluid dynamics is a subdiscipline of fluid mechanics that describes the flow of fluids— liquids and gases. It has several subdisciplines, including ''aerodynamics'' (the study of air and other gases in motion) an ...
equations, but they can also be derived from energy integrals via Lagrange's equation.
For a fluid sheet of average thickness ''D'', the vertical tidal elevation ''ζ'', as well as the horizontal velocity components ''u'' and ''v'' (in the latitude ''φ'' and longitude ''λ'' directions, respectively) satisfy Laplace's tidal equations:
:
where ''Ω'' is the angular frequency of the planet's rotation, ''g'' is the planet's gravitational acceleration at the mean ocean surface, ''a'' is the planetary radius, and ''U'' is the external gravitational tidal-forcing potential.
William Thomson (Lord Kelvin) rewrote Laplace's momentum terms using the curl
cURL (pronounced like "curl", UK: , US: ) is a computer software project providing a library (libcurl) and command-line tool (curl) for transferring data using various network protocols. The name stands for "Client URL".
History
cURL was fi ...
to find an equation for vorticity. Under certain conditions this can be further rewritten as a conservation of vorticity.
Tidal analysis and prediction
Harmonic analysis
 Laplace's improvements in theory were substantial, but they still left prediction in an approximate state. This position changed in the 1860s when the local circumstances of tidal phenomena were more fully brought into account by William Thomson's application of
Laplace's improvements in theory were substantial, but they still left prediction in an approximate state. This position changed in the 1860s when the local circumstances of tidal phenomena were more fully brought into account by William Thomson's application of Fourier analysis
In mathematics, Fourier analysis () is the study of the way general functions may be represented or approximated by sums of simpler trigonometric functions. Fourier analysis grew from the study of Fourier series, and is named after Josep ...
to the tidal motions as harmonic analysis
Harmonic analysis is a branch of mathematics concerned with the representation of Function (mathematics), functions or signals as the Superposition principle, superposition of basic waves, and the study of and generalization of the notions of Fo ...
. Thomson's work in this field was further developed and extended by George Darwin, applying the lunar theory current in his time. Darwin's symbols for the tidal harmonic constituents are still used.
Darwin's harmonic developments of the tide-generating forces were later improved when A.T. Doodson, applying the lunar theory Lunar theory attempts to account for the motions of the Moon. There are many small variations (or perturbations) in the Moon's motion, and many attempts have been made to account for them. After centuries of being problematic, lunar motion can now ...
of E.W. Brown, developed the tide-generating potential (TGP) in harmonic form, distinguishing 388 tidal frequencies. Doodson's work was carried out and published in 1921. Doodson devised a practical system for specifying the different harmonic components of the tide-generating potential, the Doodson numbers
Arthur Thomas Doodson (31 March 1890 – 10 January 1968) was a British oceanographer.
Early life
He was born at Boothstown, City of Salford, Salford, the son of cotton-mill manager Thomas Doodson. He was educated at Rochdale secondary school an ...
, a system still in use.
Since the mid-twentieth century further analysis has generated many more terms than Doodson's 388. About 62 constituents are of sufficient size to be considered for possible use in marine tide prediction, but sometimes many fewer can predict tides to useful accuracy. The calculations of tide predictions using the harmonic constituents are laborious, and from the 1870s to about the 1960s they were carried out using a mechanical tide-predicting machine, a special-purpose form of analog computer.
Tidal constituents
 Tidal constituents combine to give an endlessly varying aggregate because of their different and incommensurable frequencies: the effect is visualized in a
Tidal constituents combine to give an endlessly varying aggregate because of their different and incommensurable frequencies: the effect is visualized in aanimation of the American Mathematical Society
illustrating the way in which the components used to be mechanically combined in the tide-predicting machine. Amplitudes (half of
peak-to-peak amplitude
The amplitude of a periodic variable is a measure of its change in a single period (such as time or spatial period). The amplitude of a non-periodic signal is its magnitude compared with a reference value. There are various definitions of amplit ...
) of tidal constituents are given below for six example locations:
Eastport, Maine (ME), Biloxi, Mississippi (MS), San Juan, Puerto Rico (PR), Kodiak, Alaska (AK), San Francisco, California (CA), and Hilo, Hawaii
Hilo () is a census-designated place (CDP) and the largest settlement in Hawaii County, Hawaii, United States, which encompasses the Island of Hawaii. The population was 44,186 according to the 2020 census. It is the fourth-largest settlement i ...
(HI).
Semi-diurnal
Diurnal
Long period
Short period
Doodson numbers
In order to specify the different harmonic components of the tide-generating potential, Doodson devised a practical system which is still in use, involving what are called the Doodson numbers based on the six "Doodson arguments" or Doodson variables. The number of different tidal frequencies is large, but they can all be specified on the basis of combinations of small-integer multiples, positive or negative, of six basic angular arguments. In principle, the basic arguments can be specified in numerous ways; Doodson's choice of his six "Doodson arguments" has been widely used in tidal work. In terms of these Doodson arguments, each tidal frequency can then be specified as a sum made up of a small integer multiple of each of the six arguments. The resulting six small integer multipliers effectively encode the frequency of the tidal argument concerned, and these are the Doodson numbers: in practice all except the first are usually biased upwards by +5 to avoid negative numbers in the notation. (In the case that the biased multiple exceeds 9, the system adopts X for 10, and E for 11.) The Doodson arguments are specified in the following way, in order of decreasing frequency: and T D Moyer (2003) already cited. : is 'Mean Lunar Time', the Greenwich Hour Angle of the mean Moon plus 12 hours. : is the mean longitude of the Moon. : is the mean longitude of the Sun. : is the longitude of the Moon's mean perigee. : is the negative of the longitude of the Moon's mean ascending node on the ecliptic. : or is the longitude of the Sun's mean perigee. In these expressions, the symbols , , and refer to an alternative set of fundamental angular arguments (usually preferred for use in modern lunar theory), in which:- : is the mean anomaly of the Moon (distance from its perigee). : is the mean anomaly of the Sun (distance from its perigee). : is the Moon's mean argument of latitude (distance from its node). : is the Moon's mean elongation (distance from the sun). It is possible to define several auxiliary variables on the basis of combinations of these. In terms of this system, each tidal constituent frequency can be identified by its Doodson numbers. The strongest tidal constituent "M2" has a frequency of 2 cycles per lunar day, its Doodson numbers are usually written 255.555, meaning that its frequency is composed of twice the first Doodson argument, and zero times all of the others. The second strongest tidal constituent "S2" is influenced by the sun, and its Doodson numbers are 273.555, meaning that its frequency is composed of twice the first Doodson argument, +2 times the second, -2 times the third, and zero times each of the other three.See for example Melchior (1971), already cited, at p.191. This aggregates to the angular equivalent of mean solar time +12 hours. These two strongest component frequencies have simple arguments for which the Doodson system might appear needlessly complex, but each of the hundreds of other component frequencies can be briefly specified in a similar way, showing in the aggregate the usefulness of the encoding.See also
*Long-period tide
Long-period tides are gravitational tides with periods longer than one day, typically with amplitudes of a few centimeters or less.
Long-period tidal constituents with relatively strong forcing include the ''lunar fortnightly'' (Mf) and ''lunar m ...
* Lunar node#Effect on tides
* Kelvin wave
* Tidal table
Notes
References
External links
Contributions of satellite laser ranging to the studies of earth tides
** ttp://tidesandcurrents.noaa.gov/publications/Understanding_Tides_by_Steacy_finalFINAL11_30.pdf Understanding Tides*
150 Years of Tides on the Western Coast
*
{{DEFAULTSORT:Theory Of Tides Tides Geophysics Oceanography Continuum mechanics Fluid dynamics Fluid mechanics Planetary science