Tan (trigonometry) on:
[Wikipedia]
[Google]
[Amazon]
 In mathematics, the trigonometric functions (also called circular functions, angle functions or goniometric functions) are
In mathematics, the trigonometric functions (also called circular functions, angle functions or goniometric functions) are

 If the acute angle is given, then any right triangles that have an angle of are similar to each other. This means that the ratio of any two side lengths depends only on . Thus these six ratios define six functions of , which are the trigonometric functions. In the following definitions, the
If the acute angle is given, then any right triangles that have an angle of are similar to each other. This means that the ratio of any two side lengths depends only on . Thus these six ratios define six functions of , which are the trigonometric functions. In the following definitions, the 
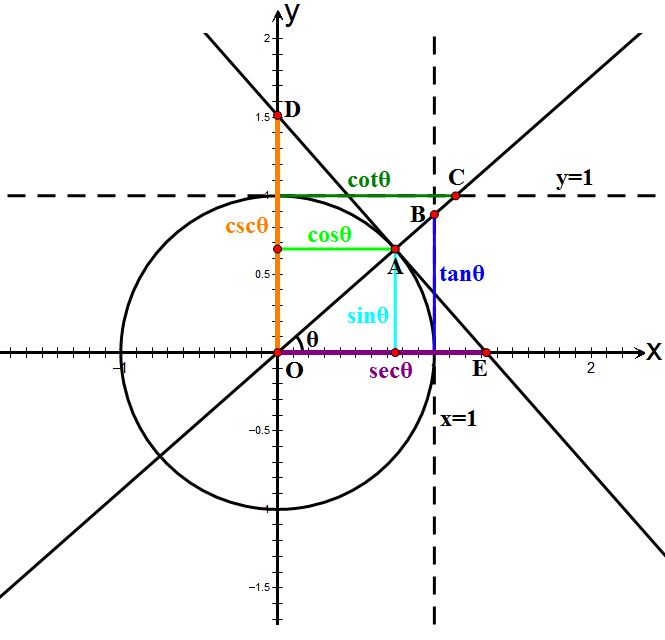 The six trigonometric functions can be defined as coordinate values of points on the
The six trigonometric functions can be defined as coordinate values of points on the  Since a rotation of an angle of does not change the position or size of a shape, the points , , , , and are the same for two angles whose difference is an integer multiple of . Thus trigonometric functions are
Since a rotation of an angle of does not change the position or size of a shape, the points , , , , and are the same for two angles whose difference is an integer multiple of . Thus trigonometric functions are
 The
The
real function
In mathematical analysis, and applications in geometry, applied mathematics, engineering, and natural sciences, a function of a real variable is a function whose domain is the real numbers \mathbb, or a subset of \mathbb that contains an inter ...
s which relate an angle of a right-angled triangle
A right triangle (American English) or right-angled triangle ( British), or more formally an orthogonal triangle, formerly called a rectangled triangle ( grc, ὀρθόσγωνία, lit=upright angle), is a triangle in which one angle is a right ...
to ratios of two side lengths. They are widely used in all sciences that are related to geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is c ...
, such as navigation
Navigation is a field of study that focuses on the process of monitoring and controlling the movement of a craft or vehicle from one place to another.Bowditch, 2003:799. The field of navigation includes four general categories: land navigation, ...
, solid mechanics
Solid mechanics, also known as mechanics of solids, is the branch of continuum mechanics that studies the behavior of solid materials, especially their motion and deformation under the action of forces, temperature changes, phase changes, and ...
, celestial mechanics
Celestial mechanics is the branch of astronomy that deals with the motions of objects in outer space. Historically, celestial mechanics applies principles of physics (classical mechanics) to astronomical objects, such as stars and planets, to ...
, geodesy
Geodesy ( ) is the Earth science of accurately measuring and understanding Earth's figure (geometric shape and size), Earth rotation, orientation in space, and Earth's gravity, gravity. The field also incorporates studies of how these properti ...
, and many others. They are among the simplest periodic function
A periodic function is a function that repeats its values at regular intervals. For example, the trigonometric functions, which repeat at intervals of 2\pi radians, are periodic functions. Periodic functions are used throughout science to d ...
s, and as such are also widely used for studying periodic phenomena through Fourier analysis.
The trigonometric functions most widely used in modern mathematics are the sine
In mathematics, sine and cosine are trigonometric functions of an angle. The sine and cosine of an acute angle are defined in the context of a right triangle: for the specified angle, its sine is the ratio of the length of the side that is opp ...
, the cosine, and the tangent. Their reciprocal
Reciprocal may refer to:
In mathematics
* Multiplicative inverse, in mathematics, the number 1/''x'', which multiplied by ''x'' gives the product 1, also known as a ''reciprocal''
* Reciprocal polynomial, a polynomial obtained from another pol ...
s are respectively the cosecant, the secant, and the cotangent, which are less used. Each of these six trigonometric functions has a corresponding inverse function
In mathematics, the inverse function of a function (also called the inverse of ) is a function that undoes the operation of . The inverse of exists if and only if is bijective, and if it exists, is denoted by f^ .
For a function f\colon ...
, and an analog among the hyperbolic functions
In mathematics, hyperbolic functions are analogues of the ordinary trigonometric functions, but defined using the hyperbola rather than the circle. Just as the points form a circle with a unit radius, the points form the right half of the ...
.
The oldest definitions of trigonometric functions, related to right-angle triangles, define them only for acute angle
In Euclidean geometry, an angle is the figure formed by two rays, called the '' sides'' of the angle, sharing a common endpoint, called the ''vertex'' of the angle.
Angles formed by two rays lie in the plane that contains the rays. Angles a ...
s. To extend the sine and cosine functions to functions whose domain
Domain may refer to:
Mathematics
*Domain of a function, the set of input values for which the (total) function is defined
** Domain of definition of a partial function
**Natural domain of a partial function
**Domain of holomorphy of a function
*Do ...
is the whole real line
In elementary mathematics, a number line is a picture of a graduated straight line that serves as visual representation of the real numbers. Every point of a number line is assumed to correspond to a real number, and every real number to a po ...
, geometrical definitions using the standard unit circle
In mathematics, a unit circle is a circle of unit radius—that is, a radius of 1. Frequently, especially in trigonometry, the unit circle is the circle of radius 1 centered at the origin (0, 0) in the Cartesian coordinate system in the Eucli ...
(i.e., a circle with radius
In classical geometry, a radius ( : radii) of a circle or sphere is any of the line segments from its center to its perimeter, and in more modern usage, it is also their length. The name comes from the latin ''radius'', meaning ray but also the ...
1 unit) are often used; then the domain of the other functions is the real line with some isolated points removed. Modern definitions express trigonometric functions as infinite series
In mathematics, a series is, roughly speaking, a description of the operation of adding infinitely many quantities, one after the other, to a given starting quantity. The study of series is a major part of calculus and its generalization, ma ...
or as solutions of differential equation
In mathematics, a differential equation is an equation that relates one or more unknown functions and their derivatives. In applications, the functions generally represent physical quantities, the derivatives represent their rates of change, a ...
s. This allows extending the domain of sine and cosine functions to the whole complex plane
In mathematics, the complex plane is the plane formed by the complex numbers, with a Cartesian coordinate system such that the -axis, called the real axis, is formed by the real numbers, and the -axis, called the imaginary axis, is formed by th ...
, and the domain of the other trigonometric functions to the complex plane with some isolated points removed.
Notation
Conventionally, an abbreviation of each trigonometric function's name is used as its symbol in formulas. Today, the most common versions of these abbreviations are "sin" for sine, "cos" for cosine, "tan" or "tg" for tangent, "sec" for secant, "csc" or "cosec" for cosecant, and "cot" or "ctg" for cotangent. Historically, these abbreviations were first used in prose sentences to indicate particularline segment
In geometry, a line segment is a part of a straight line that is bounded by two distinct end points, and contains every point on the line that is between its endpoints. The length of a line segment is given by the Euclidean distance between ...
s or their lengths related to an arc of an arbitrary circle, and later to indicate ratios of lengths, but as the function concept developed in the 17th–18th century, they began to be considered as functions of real-number-valued angle measures, and written with functional notation
In mathematics, a function from a set to a set assigns to each element of exactly one element of .; the words map, mapping, transformation, correspondence, and operator are often used synonymously. The set is called the domain of the fun ...
, for example . Parentheses are still often omitted to reduce clutter, but are sometimes necessary; for example the expression would typically be interpreted to mean so parentheses are required to express
A positive integer
In mathematics, the natural numbers are those numbers used for counting (as in "there are ''six'' coins on the table") and ordering (as in "this is the ''third'' largest city in the country").
Numbers used for counting are called '' cardinal ...
appearing as a superscript after the symbol of the function denotes exponentiation
Exponentiation is a mathematical operation, written as , involving two numbers, the '' base'' and the ''exponent'' or ''power'' , and pronounced as " (raised) to the (power of) ". When is a positive integer, exponentiation corresponds to re ...
, not function composition
In mathematics, function composition is an operation that takes two functions and , and produces a function such that . In this operation, the function is applied to the result of applying the function to . That is, the functions and ...
. For example and denote not This differs from the (historically later) general functional notation in which
However, the exponent is commonly used to denote the inverse function
In mathematics, the inverse function of a function (also called the inverse of ) is a function that undoes the operation of . The inverse of exists if and only if is bijective, and if it exists, is denoted by f^ .
For a function f\colon ...
, not the reciprocal
Reciprocal may refer to:
In mathematics
* Multiplicative inverse, in mathematics, the number 1/''x'', which multiplied by ''x'' gives the product 1, also known as a ''reciprocal''
* Reciprocal polynomial, a polynomial obtained from another pol ...
. For example and denote the inverse trigonometric function
In mathematics, the inverse trigonometric functions (occasionally also called arcus functions, antitrigonometric functions or cyclometric functions) are the inverse functions of the trigonometric functions (with suitably restricted domains). Spe ...
alternatively written The equation implies not In this case, the superscript ''could'' be considered as denoting a composed or iterated function
In mathematics, an iterated function is a function (that is, a function from some set to itself) which is obtained by composing another function with itself a certain number of times. The process of repeatedly applying the same function ...
, but negative superscripts other than are not in common use.
Right-angled triangle definitions
hypotenuse
In geometry, a hypotenuse is the longest side of a right-angled triangle, the side opposite the right angle. The length of the hypotenuse can be found using the Pythagorean theorem, which states that the square of the length of the hypotenuse eq ...
is the length of the side opposite the right angle, ''opposite'' represents the side opposite the given angle , and ''adjacent'' represents the side between the angle and the right angle.
In a right-angled triangle, the sum of the two acute angles is a right angle, that is, or . Therefore and represent the same ratio, and thus are equal. This identity and analogous relationships between the other trigonometric functions are summarized in the following table.
Radians versus degrees
In geometric applications, the argument of a trigonometric function is generally the measure of anangle
In Euclidean geometry, an angle is the figure formed by two rays, called the '' sides'' of the angle, sharing a common endpoint, called the '' vertex'' of the angle.
Angles formed by two rays lie in the plane that contains the rays. Angles ...
. For this purpose, any angular unit
In Euclidean geometry, an angle is the figure formed by two rays, called the '' sides'' of the angle, sharing a common endpoint, called the ''vertex'' of the angle.
Angles formed by two rays lie in the plane that contains the rays. Angles a ...
is convenient, and angles are most commonly measured in conventional units of degrees
Degree may refer to:
As a unit of measurement
* Degree (angle), a unit of angle measurement
** Degree of geographical latitude
** Degree of geographical longitude
* Degree symbol (°), a notation used in science, engineering, and mathematics
...
in which a right angle is 90° and a complete turn is 360° (particularly in elementary mathematics
Elementary mathematics consists of mathematics topics frequently taught at the primary or secondary school levels.
In the Canadian curriculum, there are six basic strands in Elementary Mathematics: Number, Algebra, Data, Spatial Sense, Fin ...
).
However, in calculus
Calculus, originally called infinitesimal calculus or "the calculus of infinitesimals", is the mathematics, mathematical study of continuous change, in the same way that geometry is the study of shape, and algebra is the study of generalizati ...
and mathematical analysis
Analysis is the branch of mathematics dealing with continuous functions, limit (mathematics), limits, and related theories, such as Derivative, differentiation, Integral, integration, measure (mathematics), measure, infinite sequences, series (m ...
, the trigonometric functions are generally regarded more abstractly as functions of real
Real may refer to:
Currencies
* Brazilian real (R$)
* Central American Republic real
* Mexican real
* Portuguese real
* Spanish real
* Spanish colonial real
Music Albums
* ''Real'' (L'Arc-en-Ciel album) (2000)
* ''Real'' (Bright album) (201 ...
or complex number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the for ...
s, rather than angles. In fact, the functions sin and cos can be defined for all complex numbers in terms of the exponential function
The exponential function is a mathematical function denoted by f(x)=\exp(x) or e^x (where the argument is written as an exponent). Unless otherwise specified, the term generally refers to the positive-valued function of a real variable, ...
via power series or as solutions to differential equation
In mathematics, a differential equation is an equation that relates one or more unknown functions and their derivatives. In applications, the functions generally represent physical quantities, the derivatives represent their rates of change, a ...
s given particular initial values (''see below''), without reference to any geometric notions. The other four trigonometric functions (tan, cot, sec, csc) can be defined as quotients and reciprocals of sin and cos, except where zero occurs in the denominator. It can be proved, for real arguments, that these definitions coincide with elementary geometric definitions ''if'' ''the argument is regarded as an angle given in radians''. Moreover, these definitions result in simple expressions for the derivative
In mathematics, the derivative of a function of a real variable measures the sensitivity to change of the function value (output value) with respect to a change in its argument (input value). Derivatives are a fundamental tool of calculus. ...
s and indefinite integrals
In calculus, an antiderivative, inverse derivative, primitive function, primitive integral or indefinite integral of a function is a differentiable function whose derivative is equal to the original function . This can be stated symbolically ...
for the trigonometric functions. Thus, in settings beyond elementary geometry, radians are regarded as the mathematically natural unit for describing angle measures.
When radian
The radian, denoted by the symbol rad, is the unit of angle in the International System of Units (SI) and is the standard unit of angular measure used in many areas of mathematics. The unit was formerly an SI supplementary unit (before tha ...
s (rad) are employed, the angle is given as the length of the arc of the unit circle
In mathematics, a unit circle is a circle of unit radius—that is, a radius of 1. Frequently, especially in trigonometry, the unit circle is the circle of radius 1 centered at the origin (0, 0) in the Cartesian coordinate system in the Eucli ...
subtended by it: the angle that subtends an arc of length 1 on the unit circle is 1 rad (≈ 57.3°), and a complete turn
Turn may refer to:
Arts and entertainment
Dance and sports
* Turn (dance and gymnastics), rotation of the body
* Turn (swimming), reversing direction at the end of a pool
* Turn (professional wrestling), a transition between face and heel
* Turn, ...
(360°) is an angle of 2 (≈ 6.28) rad. For real number ''x'', the notations sin ''x'', cos ''x'', etc. refer to the value of the trigonometric functions evaluated at an angle of ''x'' rad. If units of degrees are intended, the degree sign must be explicitly shown (e.g., sin ''x°'', cos ''x°'', etc.). Using this standard notation, the argument ''x'' for the trigonometric functions satisfies the relationship ''x'' = (180''x''/)°, so that, for example, sin = sin 180° when we take ''x'' = . In this way, the degree symbol can be regarded as a mathematical constant such that 1° = /180 ≈ 0.0175.
Unit-circle definitions
 The six trigonometric functions can be defined as coordinate values of points on the
The six trigonometric functions can be defined as coordinate values of points on the Euclidean plane
In mathematics, the Euclidean plane is a Euclidean space of dimension two. That is, a geometric setting in which two real quantities are required to determine the position of each point ( element of the plane), which includes affine notions ...
that are related to the unit circle
In mathematics, a unit circle is a circle of unit radius—that is, a radius of 1. Frequently, especially in trigonometry, the unit circle is the circle of radius 1 centered at the origin (0, 0) in the Cartesian coordinate system in the Eucli ...
, which is the circle
A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre. Equivalently, it is the curve traced out by a point that moves in a plane so that its distance from a given point is const ...
of radius one centered at the origin of this coordinate system. While right-angled triangle definitions allow for the definition of the trigonometric functions for angles between and radian
The radian, denoted by the symbol rad, is the unit of angle in the International System of Units (SI) and is the standard unit of angular measure used in many areas of mathematics. The unit was formerly an SI supplementary unit (before tha ...
s the unit circle definitions allow the domain of trigonometric functions to be extended to all positive and negative real numbers.
Let be the ray
Ray may refer to:
Fish
* Ray (fish), any cartilaginous fish of the superorder Batoidea
* Ray (fish fin anatomy), a bony or horny spine on a fin
Science and mathematics
* Ray (geometry), half of a line proceeding from an initial point
* Ray (gra ...
obtained by rotating by an angle the positive half of the -axis (counterclockwise
Two-dimensional rotation can occur in two possible directions. Clockwise motion (abbreviated CW) proceeds in the same direction as a clock's hands: from the top to the right, then down and then to the left, and back up to the top. The opposite s ...
rotation for and clockwise rotation for ). This ray intersects the unit circle at the point The ray extended to a line
Line most often refers to:
* Line (geometry), object with zero thickness and curvature that stretches to infinity
* Telephone line, a single-user circuit on a telephone communication system
Line, lines, The Line, or LINE may also refer to:
Art ...
if necessary, intersects the line of equation at point and the line of equation at point The tangent line
In geometry, the tangent line (or simply tangent) to a plane curve at a given point is the straight line that "just touches" the curve at that point. Leibniz defined it as the line through a pair of infinitely close points on the curve. More ...
to the unit circle at the point , is perpendicular
In elementary geometry, two geometric objects are perpendicular if they intersect at a right angle (90 degrees or π/2 radians). The condition of perpendicularity may be represented graphically using the ''perpendicular symbol'', ⟂. It can ...
to and intersects the - and -axes at points and The coordinates
In geometry, a coordinate system is a system that uses one or more numbers, or coordinates, to uniquely determine the position of the points or other geometric elements on a manifold such as Euclidean space. The order of the coordinates is si ...
of these points give the values of all trigonometric functions for any arbitrary real value of in the following manner.
The trigonometric functions and are defined, respectively, as the ''x''- and ''y''-coordinate values of point . That is,
: and
In the range , this definition coincides with the right-angled triangle definition, by taking the right-angled triangle to have the unit radius as hypotenuse
In geometry, a hypotenuse is the longest side of a right-angled triangle, the side opposite the right angle. The length of the hypotenuse can be found using the Pythagorean theorem, which states that the square of the length of the hypotenuse eq ...
. And since the equation holds for all points on the unit circle, this definition of cosine and sine also satisfies the Pythagorean identity
The Pythagorean trigonometric identity, also called simply the Pythagorean identity, is an identity expressing the Pythagorean theorem in terms of trigonometric functions. Along with the sum-of-angles formulae, it is one of the basic relations be ...
.
:
The other trigonometric functions can be found along the unit circle as
: and
: and
By applying the Pythagorean identity and geometric proof methods, these definitions can readily be shown to coincide with the definitions of tangent, cotangent, secant and cosecant in terms of sine and cosine, that is
:
periodic function
A periodic function is a function that repeats its values at regular intervals. For example, the trigonometric functions, which repeat at intervals of 2\pi radians, are periodic functions. Periodic functions are used throughout science to d ...
s with period . That is, the equalities
: and
hold for any angle and any integer
An integer is the number zero (), a positive natural number (, , , etc.) or a negative integer with a minus sign ( −1, −2, −3, etc.). The negative numbers are the additive inverses of the corresponding positive numbers. In the language ...
. The same is true for the four other trigonometric functions. By observing the sign and the monotonicity of the functions sine, cosine, cosecant, and secant in the four quadrants, one can show that is the smallest value for which they are periodic (i.e., is the fundamental period of these functions). However, after a rotation by an angle , the points and already return to their original position, so that the tangent function and the cotangent function have a fundamental period of . That is, the equalities
: and
hold for any angle and any integer .
Algebraic values
algebraic expression In mathematics, an algebraic expression is an expression built up from integer constants, variables, and the algebraic operations ( addition, subtraction, multiplication, division and exponentiation by an exponent that is a rational number). ...
s for the most important angles are as follows:
: ( zero angle)
:
:
:
: ( right angle)
Writing the numerators as square roots
In mathematics, a square root of a number is a number such that ; in other words, a number whose ''square'' (the result of multiplying the number by itself, or ⋅ ) is . For example, 4 and −4 are square roots of 16, because .
...
of consecutive non-negative integers, with a denominator of 2, provides an easy way to remember the values.
Such simple expressions generally do not exist for other angles which are rational multiples of a right angle.
*For an angle which, measured in degrees, is a multiple of three, the exact trigonometric values
In mathematics, the values of the trigonometric functions can be expressed approximately, as in \cos (\pi/4) \approx 0.707, or exactly, as in \cos (\pi/ 4)= \sqrt 2 /2. While trigonometric tables contain many approximate values, the exact values ...
of the sine and the cosine may be expressed in terms of square roots. These values of the sine and the cosine may thus be constructed by ruler and compass
In geometry, straightedge-and-compass construction – also known as ruler-and-compass construction, Euclidean construction, or classical construction – is the construction of lengths, angles, and other geometric figures using only an ideali ...
.
*For an angle of an integer number of degrees, the sine and the cosine may be expressed in terms of square roots and the cube root of a non-real complex number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the for ...
. Galois theory
In mathematics, Galois theory, originally introduced by Évariste Galois, provides a connection between field theory and group theory. This connection, the fundamental theorem of Galois theory, allows reducing certain problems in field theory t ...
allows a proof that, if the angle is not a multiple of 3°, non-real cube roots are unavoidable.
*For an angle which, expressed in degrees, is a rational number
In mathematics, a rational number is a number that can be expressed as the quotient or fraction of two integers, a numerator and a non-zero denominator . For example, is a rational number, as is every integer (e.g. ). The set of all ra ...
, the sine and the cosine are algebraic number
An algebraic number is a number that is a root of a non-zero polynomial in one variable with integer (or, equivalently, rational) coefficients. For example, the golden ratio, (1 + \sqrt)/2, is an algebraic number, because it is a root of the p ...
s, which may be expressed in terms of th roots. This results from the fact that the Galois group
In mathematics, in the area of abstract algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension. The study of field extensions and their relationship to the po ...
s of the cyclotomic polynomial
In mathematics, the ''n''th cyclotomic polynomial, for any positive integer ''n'', is the unique irreducible polynomial with integer coefficients that is a divisor of x^n-1 and is not a divisor of x^k-1 for any Its roots are all ''n''th primit ...
s are cyclic
Cycle, cycles, or cyclic may refer to:
Anthropology and social sciences
* Cyclic history, a theory of history
* Cyclical theory, a theory of American political history associated with Arthur Schlesinger, Sr.
* Social cycle, various cycles in so ...
.
*For an angle which, expressed in degrees, is not a rational number, then either the angle or both the sine and the cosine are