T-J Model

In solid-state physics, the ''t''-''J'' model is a model first derived in 1977 from the Hubbard model by Józef Spałek to explain antiferromagnetic properties of the Mott insulators and taking into account experimental results about the strength of electron-electron repulsion in this materials. 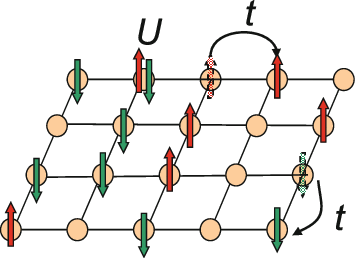The model consider the materials as a lattice with atoms in the knots (sites) and just one or two external electrons moving among them (internal electrons are not considered), like in the basic Hubbard model. That difference is in supposing electrons being strongly-correlated, that means electrons are very sensible to reciprocal coulombic repulsion, and so are more constrained to avoid occupying lattice's sites already occupied by another electron. In the basic Hubbard model, the repulsion, indicated with ''U'', can be small and also null, and electrons are freer to jump (''hopping'', parametrized by ''t'' as ''transfer'' or ''tunnel'') from one site to another. In the ''t''-''J'' model, instead of ''U'', there is the parameter ''J'', function of the ratio ''t''/''U'', so the name.

It is used as a possible model to explain high temperature superconductivity in doped antiferromagnets, in the hypothesis of strong coupling between electrons.

The Hamiltonian

In quantum physics system's models are usually based on the Hamiltonian operator $\hat H$, corresponding to the total energy of that system, including both kinetic energy and potential energy.

The ''t''-''J'' Hamiltonian can be derived from the $\hat H$ of the Hubbard model using the Schrieffer–Wolff transformation, with the transformation generator depending on ''t''/''U'' and excluding the possibility for electrons to doubly occupy a lattice's site, which results in:

:$\hat H = -t\sum_ \left( c_^ c_ + \mathrm \right) + \fracJ\sum_\left(\mathbf_\cdot \mathbf_-\frac\right) + O(t^3/U^2)$

where the term in ''t'' corresponds to the kinetic energy and is equal to the one in the Hubbard model. The second one is the potential energy approximated at the second order, because this is an approximation of the Hubbard model in the limit ''U'' >> ''t'' developed in power of ''t''. Terms at higher order can be added.

The parameters are:
* is the sum over nearest-neighbor sites ''i'' and ''j'', for all sites, typically on a two-dimensional square lattice,
*''c'', ''c'' are the fermionic creation and annihilation operators at site ''i'',
*''σ'' is the spin polarization,
*''t'' is the hopping integral,
*''J'' is the antiferromagnetic exchange coupling, ''J'' = ,
*''U'' is the on-site coulombic repulsion, that must satisfy the condition for ''U'' >> ''t'',
*''n_i'' = ''c'c'' is the particle number at site ''i'' and can be maximum 1, so that double occupancy is forbidden (in the Hubbard model is possible),
*S_''i'' and S_''j'' are the spins on sites ''i'' and ''j'',
*h. c. stands for Hermitian conjugate,
If ''n_i'' = 1, that is when in the ground state, there is just one electron per lattice's site (half-filling), the model reduces to the Heisenberg model and the ground state reproduce a dielectric antiferromagnets (Mott insulator).

The model can be further extended considering also the next-nearest-neighbor sites and the chemical potential to set the ground state in function of the total number of particles:

:$\mathcal = t_1 \sum\limits_ \left( c_^ c_ + \mathrm \right) \ + \ t_2 \sum\limits_ \left( c_^ c_ + \mathrm \right) \ + \ J \sum\limits_ \left( \mathbf_ \cdot \mathbf_ - \frac\right) - \ \mu\sum\limits_ n_ ,$

where ⟨...⟩ and ⟨⟨...⟩⟩ denote the nearest and next-nearest neighbors, respectively, with two different values for the hopping integral (''t''₁ and ''t''₂) and ''μ'' is the chemical potential.

References

Further reading

*
*
* {{Citation , last=Dr Mitchell , title=Electron interactions and the Hubbard model , url=https://www.youtube.com/watch?v=wtYQlELm3tk , language=en , access-date=2022-08-29

Lattice models