Storey-Tibshirani Procedure on:
[Wikipedia]
[Google]
[Amazon]
In 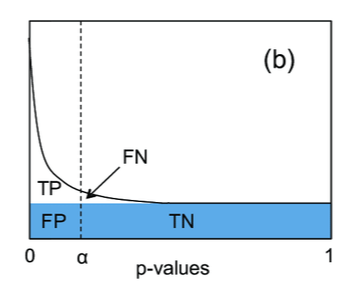
qvalue
package in R estimates ''q''-values from a list of ''p''-values.
statistical hypothesis testing
A statistical hypothesis test is a method of statistical inference used to decide whether the data provide sufficient evidence to reject a particular hypothesis. A statistical hypothesis test typically involves a calculation of a test statistic. T ...
, specifically multiple hypothesis testing, the ''q''-value in the Storey procedure provides a means to control the positive false discovery rate (pFDR). Just as the ''p''-value gives the expected false positive rate obtained by rejecting the null hypothesis
The null hypothesis (often denoted ''H''0) is the claim in scientific research that the effect being studied does not exist. The null hypothesis can also be described as the hypothesis in which no relationship exists between two sets of data o ...
for any result with an equal or smaller ''p''-value, the ''q''-value gives the expected pFDR obtained by rejecting the null hypothesis for any result with an equal or smaller ''q''-value.

History
In statistics, testing multiple hypotheses simultaneously using methods appropriate for testing single hypotheses tends to yield many false positives: the so-calledmultiple comparisons problem
Multiple comparisons, multiplicity or multiple testing problem occurs in statistics when one considers a set of statistical inferences simultaneously or estimates a subset of parameters selected based on the observed values.
The larger the numbe ...
. For example, assume that one were to test 1,000 null hypotheses, all of which are true, and (as is conventional in single hypothesis testing) to reject null hypotheses with a significance level
In statistical hypothesis testing, a result has statistical significance when a result at least as "extreme" would be very infrequent if the null hypothesis were true. More precisely, a study's defined significance level, denoted by \alpha, is the ...
of 0.05; due to random chance, one would expect 5% of the results to appear significant ('' P'' < 0.05), yielding 50 false positives (rejections of the null hypothesis). Since the 1950s, statisticians had been developing methods for multiple comparisons that reduced the number of false positives, such as controlling the family-wise error rate
In statistics, family-wise error rate (FWER) is the probability of making one or more false discoveries, or type I errors when performing multiple hypotheses tests.
Familywise and experimentwise error rates
John Tukey developed in 1953 the conce ...
(FWER) using the Bonferroni correction
In statistics, the Bonferroni correction is a method to counteract the multiple comparisons problem.
Background
The method is named for its use of the Bonferroni inequalities.
Application of the method to confidence intervals was described by ...
, but these methods also increased the number of false negatives (i.e. reduced the statistical power
In frequentist statistics, power is the probability of detecting a given effect (if that effect actually exists) using a given test in a given context. In typical use, it is a function of the specific test that is used (including the choice of tes ...
). In 1995, Yoav Benjamini and Yosef Hochberg proposed controlling the false discovery rate
In statistics, the false discovery rate (FDR) is a method of conceptualizing the rate of type I errors in null hypothesis testing when conducting multiple comparisons. FDR-controlling procedures are designed to control the FDR, which is the exp ...
(FDR) as a more statistically powerful alternative to controlling the FWER in multiple hypothesis testing. The pFDR and the ''q-''value were introduced by John D. Storey in 2002 in order to improve upon a limitation of the FDR, namely that the FDR is not defined when there are no positive results.
Definition
Let there be a null hypothesis and analternative hypothesis
In statistical hypothesis testing, the alternative hypothesis is one of the proposed propositions in the hypothesis test. In general the goal of hypothesis test is to demonstrate that in the given condition, there is sufficient evidence supporting ...
. Perform hypothesis tests; let the test statistic
Test statistic is a quantity derived from the sample for statistical hypothesis testing.Berger, R. L.; Casella, G. (2001). ''Statistical Inference'', Duxbury Press, Second Edition (p.374) A hypothesis test is typically specified in terms of a tes ...
s be i.i.d. random variables such that . That is, if is true for test (), then follows the null distribution
Null may refer to:
Science, technology, and mathematics Astronomy
*Nuller, an optical tool using interferometry to block certain sources of light Computing
*Null (SQL) (or NULL), a special marker and keyword in SQL indicating that a data value do ...
; while if is true (), then follows the alternative distribution . Let , that is, for each test, is true with probability and is true with probability . Denote the critical region
A statistical hypothesis test is a method of statistical inference used to decide whether the data provide sufficient evidence to reject a particular hypothesis. A statistical hypothesis test typically involves a calculation of a test statistic. T ...
(the values of for which is rejected) at significance level
In statistical hypothesis testing, a result has statistical significance when a result at least as "extreme" would be very infrequent if the null hypothesis were true. More precisely, a study's defined significance level, denoted by \alpha, is the ...
by . Let an experiment yield a value for the test statistic. The ''q''-value of is formally defined as
:
That is, the ''q''-value is the infimum
In mathematics, the infimum (abbreviated inf; : infima) of a subset S of a partially ordered set P is the greatest element in P that is less than or equal to each element of S, if such an element exists. If the infimum of S exists, it is unique ...
of the pFDR if is rejected for test statistics with values . Equivalently, the ''q''-value equals
:
which is the infimum of the probability that is true given that is rejected (the false discovery rate
In statistics, the false discovery rate (FDR) is a method of conceptualizing the rate of type I errors in null hypothesis testing when conducting multiple comparisons. FDR-controlling procedures are designed to control the FDR, which is the exp ...
).
Relationship to the ''p''-value
The ''p''-value is defined as : the infimum of the probability that is rejected given that is true (the false positive rate). Comparing the definitions of the ''p''- and ''q''-values, it can be seen that the ''q''-value is the minimumposterior probability
The posterior probability is a type of conditional probability that results from updating the prior probability with information summarized by the likelihood via an application of Bayes' rule. From an epistemological perspective, the posteri ...
that is true.
Interpretation
The ''q''-value can be interpreted as thefalse discovery rate
In statistics, the false discovery rate (FDR) is a method of conceptualizing the rate of type I errors in null hypothesis testing when conducting multiple comparisons. FDR-controlling procedures are designed to control the FDR, which is the exp ...
(FDR): the proportion of false positives among all positive results. Given a set of test statistics and their associated ''q''-values, rejecting the null hypothesis for all tests whose ''q''-value is less than or equal to some threshold ensures that the expected value of the false discovery rate is .
Applications
Biology
Gene expression
Genome-wide analyses of differential gene expression involve simultaneously testing the expression of thousands of genes. Controlling the FWER (usually to 0.05) avoids excessive false positives (i.e. detecting differential expression in a gene that is not differentially expressed) but imposes a strict threshold for the ''p''-value that results in many false negatives (many differentially expressed genes are overlooked). However, controlling the pFDR by selecting genes with significant ''q''-values lowers the number of false negatives (increases the statistical power) while ensuring that the expected value of the proportion of false positives among all positive results is low (e.g. 5%). For example, suppose that among 10,000 genes tested, 1,000 are actually differentially expressed and 9,000 are not: * If we consider every gene with a ''p''-value of less than 0.05 to be differentially expressed, we expect that 450 (5%) of the 9,000 genes that are not differentially expressed will appear to be differentially expressed (450 false positives). * If we control the FWER to 0.05, there is only a 5% probability of obtaining at least one false positive. However, this very strict criterion will reduce the power such that few of the 1,000 genes that are actually differentially expressed will appear to be differentially expressed (many false negatives). * If we control the pFDR to 0.05 by considering all genes with a ''q''-value of less than 0.05 to be differentially expressed, then we expect 5% of the positive results to be false positives (e.g. 900 true positives, 45 false positives, 100 false negatives, 8,955 true negatives). This strategy enables one to obtain relatively low numbers of both false positives and false negatives.Implementations
Note: the following is an incomplete list.R
* Thqvalue
package in R estimates ''q''-values from a list of ''p''-values.
References
{{reflist Multiple comparisons Statistical hypothesis testing