Stereographic Projection on:
[Wikipedia]
[Google]
[Amazon]
In
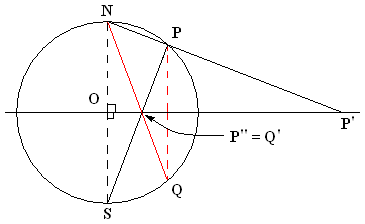 The stereographic projection relates to the plane inversion in a simple way. Let and be two points on the sphere with projections and on the plane. Then and are inversive images of each other in the image of the equatorial circle if and only if and are reflections of each other in the equatorial plane.
In other words, if:
* is a point on the sphere, but not a 'north pole' and not its antipode, the 'south pole' ,
* is the image of in a stereographic projection with the projection point and
* is the image of in a stereographic projection with the projection point ,
then and are inversive images of each other in the unit circle.
:
The stereographic projection relates to the plane inversion in a simple way. Let and be two points on the sphere with projections and on the plane. Then and are inversive images of each other in the image of the equatorial circle if and only if and are reflections of each other in the equatorial plane.
In other words, if:
* is a point on the sphere, but not a 'north pole' and not its antipode, the 'south pole' ,
* is the image of in a stereographic projection with the projection point and
* is the image of in a stereographic projection with the projection point ,
then and are inversive images of each other in the unit circle.
:
 Stereographic projection plots can be carried out by a computer using the explicit formulas given above. However, for graphing by hand these formulas are unwieldy. Instead, it is common to use graph paper designed specifically for the task. This special graph paper is called a stereonet or Wulff net, after the Russian mineralogist George (Yuri Viktorovich) Wulff.
The Wulff net shown here is the stereographic projection of the grid of parallels and meridians of a hemisphere centred at a point on the
Stereographic projection plots can be carried out by a computer using the explicit formulas given above. However, for graphing by hand these formulas are unwieldy. Instead, it is common to use graph paper designed specifically for the task. This special graph paper is called a stereonet or Wulff net, after the Russian mineralogist George (Yuri Viktorovich) Wulff.
The Wulff net shown here is the stereographic projection of the grid of parallels and meridians of a hemisphere centred at a point on the
Image:Wulff net central angle 1.jpg, Two points and are drawn on a transparent sheet tacked at the origin of a Wulff net.
Image:Wulff net central angle 2.jpg, The transparent sheet is rotated and the central angle is read along the common meridian to both points and .
 Although any stereographic projection misses one point on the sphere (the projection point), the entire sphere can be mapped using two projections from distinct projection points. In other words, the sphere can be covered by two stereographic parametrizations (the inverses of the projections) from the plane. The parametrizations can be chosen to induce the same orientation on the sphere. Together, they describe the sphere as an oriented surface (or two-dimensional
Although any stereographic projection misses one point on the sphere (the projection point), the entire sphere can be mapped using two projections from distinct projection points. In other words, the sphere can be covered by two stereographic parametrizations (the inverses of the projections) from the plane. The parametrizations can be chosen to induce the same orientation on the sphere. Together, they describe the sphere as an oriented surface (or two-dimensional
 The pair of trigonometric functions can be thought of as parametrizing the unit circle. The stereographic projection gives an alternative parametrization of the unit circle:
:
Under this reparametrization, the length element of the unit circle goes over to
:
This substitution can sometimes simplify
The pair of trigonometric functions can be thought of as parametrizing the unit circle. The stereographic projection gives an alternative parametrization of the unit circle:
:
Under this reparametrization, the length element of the unit circle goes over to
:
This substitution can sometimes simplify
File:Stereographic projection SW.JPG, Stereographic projection of the world north of 30°S. 15° graticule.
File:Stereographic with Tissot's Indicatrices of Distortion.svg, The stereographic projection with
 Researchers in
Researchers in
 Some
Some
Stereographic Projection and Inversion
from
DoITPoMS Teaching and Learning Package - "The Stereographic Projection"
Proof about Stereographic Projection taking circles in the sphere to circles in the plane
*
Stereonet
a software tool for structural geology by Rick Allmendinger.
PTCLab
the phase transformation crystallography lab
Sphaerica
software tool for straightedge and compass construction on the sphere, including a stereographic projection display option
Estereografica Web
a web application for stereographic projection in structural geology and fault kinematics by Ernesto Cristallini. {{Authority control Conformal mappings Conformal projections Crystallography Projective geometry
mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many ar ...
, a stereographic projection is a perspective projection of the sphere
A sphere (from Ancient Greek, Greek , ) is a surface (mathematics), surface analogous to the circle, a curve. In solid geometry, a sphere is the Locus (mathematics), set of points that are all at the same distance from a given point in three ...
, through a specific point on the sphere (the ''pole'' or ''center of projection''), onto a plane (the ''projection plane'') perpendicular
In geometry, two geometric objects are perpendicular if they intersect at right angles, i.e. at an angle of 90 degrees or π/2 radians. The condition of perpendicularity may be represented graphically using the '' perpendicular symbol'', ⟠...
to the diameter
In geometry, a diameter of a circle is any straight line segment that passes through the centre of the circle and whose endpoints lie on the circle. It can also be defined as the longest Chord (geometry), chord of the circle. Both definitions a ...
through the point. It is a smooth, bijective
In mathematics, a bijection, bijective function, or one-to-one correspondence is a function between two sets such that each element of the second set (the codomain) is the image of exactly one element of the first set (the domain). Equival ...
function from the entire sphere except the center of projection to the entire plane. It maps circles on the sphere to circles or lines on the plane, and is conformal, meaning that it preserves angle
In Euclidean geometry, an angle can refer to a number of concepts relating to the intersection of two straight Line (geometry), lines at a Point (geometry), point. Formally, an angle is a figure lying in a Euclidean plane, plane formed by two R ...
s at which curves meet and thus locally approximately preserves shapes. It is neither isometric (distance preserving) nor equiareal (area preserving).
The stereographic projection gives a way to represent a sphere by a plane. The metric induced by the inverse stereographic projection from the plane to the sphere defines a geodesic distance between points in the plane equal to the spherical distance between the spherical points they represent. A two-dimensional coordinate system
In geometry, a coordinate system is a system that uses one or more numbers, or coordinates, to uniquely determine and standardize the position of the points or other geometric elements on a manifold such as Euclidean space. The coordinates are ...
on the stereographic plane is an alternative setting for spherical analytic geometry
In mathematics, analytic geometry, also known as coordinate geometry or Cartesian geometry, is the study of geometry using a coordinate system. This contrasts with synthetic geometry.
Analytic geometry is used in physics and engineering, and als ...
instead of spherical polar coordinates or three-dimensional cartesian coordinates
In geometry, a Cartesian coordinate system (, ) in a plane is a coordinate system that specifies each point uniquely by a pair of real numbers called ''coordinates'', which are the signed distances to the point from two fixed perpendicular o ...
. This is the spherical analog of the Poincaré disk model
In geometry, the Poincaré disk model, also called the conformal disk model, is a model of 2-dimensional hyperbolic geometry in which all points are inside the unit disk, and straight lines are either circular arcs contained within the disk t ...
of the hyperbolic plane.
Intuitively, the stereographic projection is a way of picturing the sphere as the plane, with some inevitable compromises. Because the sphere and the plane appear in many areas of mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many ar ...
and its applications, so does the stereographic projection; it finds use in diverse fields including complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is helpful in many branches of mathematics, including algebraic ...
, cartography
Cartography (; from , 'papyrus, sheet of paper, map'; and , 'write') is the study and practice of making and using maps. Combining science, aesthetics and technique, cartography builds on the premise that reality (or an imagined reality) can ...
, geology
Geology (). is a branch of natural science concerned with the Earth and other astronomical objects, the rocks of which they are composed, and the processes by which they change over time. Modern geology significantly overlaps all other Earth ...
, and photography
Photography is the visual arts, art, application, and practice of creating images by recording light, either electronically by means of an image sensor, or chemically by means of a light-sensitive material such as photographic film. It is empl ...
. Sometimes stereographic computations are done graphically using a special kind of graph paper called a stereographic net, shortened to stereonet, or Wulff net.
History
The origin of the stereographic projection is not known, but it is believed to have been discovered by Ancient Greek astronomers and used for projecting thecelestial sphere
In astronomy and navigation, the celestial sphere is an abstract sphere that has an arbitrarily large radius and is concentric to Earth. All objects in the sky can be conceived as being projected upon the inner surface of the celestial sphere, ...
to the plane so that the motions of stars and planets could be analyzed using plane geometry. Its earliest extant description is found in Ptolemy
Claudius Ptolemy (; , ; ; – 160s/170s AD) was a Greco-Roman mathematician, astronomer, astrologer, geographer, and music theorist who wrote about a dozen scientific treatises, three of which were important to later Byzantine science, Byzant ...
's ''Planisphere'' (2nd century AD), but it was ambiguously attributed to Hipparchus
Hipparchus (; , ; BC) was a Ancient Greek astronomy, Greek astronomer, geographer, and mathematician. He is considered the founder of trigonometry, but is most famous for his incidental discovery of the precession of the equinoxes. Hippar ...
(2nd century BC) by Synesius (), Synesius wrote in a letter describing an instrument involving the stereographic projection: "Hipparchus long ago hinted at the unfolding of a spherical surface n a plane so as to keep a proper proportion between the given ratios in the different figures, and he was in fact the first to apply himself to this subject. I, however (if it is not presumptuous to make so great a claim), have followed it to its uttermost conclusion, and have perfected it, although for most of the intervening time the problem had been neglected; for the great Ptolemy and the divine band of his successors were content to make only such use of it as sufficed for the night-clock by means of the sixteen stars, which were the only ones that Hipparchus rearranged and entered on his instrument." Translation from , fragment 63 pp. 102–103. Dicks concludes (commentary on fragment 63, pp. 194–207): "Whether Synesius' evidence can be accepted at its face value depends on the view taken as to the strength of the objections raised above. On the whole, it would seem that the value of his testimony has been greatly exaggerated, and its unsatisfactory nature on so many points insufficiently emphasized. At any rate, the 'instrument' he sent to Paeonius was either a modified astrolabic clock of the Vitruvian type or a simple celestial map, and not a planispheric astrolabe. Furthermore, on the evidence available we are not, in my opinion, justified in attributing to Hipparchus a knowledge of either stereographic projection or the planispheric astrolabe." and Apollonius's ''Conics'' () contains a theorem
In mathematics and formal logic, a theorem is a statement (logic), statement that has been Mathematical proof, proven, or can be proven. The ''proof'' of a theorem is a logical argument that uses the inference rules of a deductive system to esta ...
which is crucial in proving the property that the stereographic projection maps circles to circles. Hipparchus, Apollonius, Archimedes
Archimedes of Syracuse ( ; ) was an Ancient Greece, Ancient Greek Greek mathematics, mathematician, physicist, engineer, astronomer, and Invention, inventor from the ancient city of Syracuse, Sicily, Syracuse in History of Greek and Hellenis ...
, and even Eudoxus (4th century BC) have sometimes been speculatively credited with inventing or knowing of the stereographic projection, but some experts consider these attributions unjustified. Ptolemy refers to the use of the stereographic projection in a "horoscopic instrument", perhaps the described by Vitruvius
Vitruvius ( ; ; –70 BC – after ) was a Roman architect and engineer during the 1st century BC, known for his multi-volume work titled . As the only treatise on architecture to survive from antiquity, it has been regarded since the Renaissan ...
(1st century BC).
By the time of Theon of Alexandria (4th century), the planisphere had been combined with a dioptra to form the planispheric astrolabe ("star taker"), a capable portable device which could be used for measuring star positions and performing a wide variety of astronomical calculations. The astrolabe was in continuous use by Byzantine
The Byzantine Empire, also known as the Eastern Roman Empire, was the continuation of the Roman Empire centred on Constantinople during late antiquity and the Middle Ages. Having survived the events that caused the fall of the Western Roman E ...
astronomers, and was significantly further developed by medieval Islamic astronomers. It was transmitted to Western Europe during the 11th–12th century, with Arabic texts translated into Latin.
In the 16th and 17th century, the equator
The equator is the circle of latitude that divides Earth into the Northern Hemisphere, Northern and Southern Hemisphere, Southern Hemispheres of Earth, hemispheres. It is an imaginary line located at 0 degrees latitude, about in circumferen ...
ial aspect of the stereographic projection was commonly used for maps of the Eastern and Western Hemisphere
The Western Hemisphere is the half of the planet Earth that lies west of the Prime Meridian (which crosses Greenwich, London, United Kingdom) and east of the 180th meridian.- The other half is called the Eastern Hemisphere. Geopolitically, ...
s. It is believed that already the map created in 1507 by Gualterius Lud was in stereographic projection, as were later the maps of Jean Rotz (1542), Rumold Mercator (1595), and many others.Snyder (1989). In star charts, even this equatorial aspect had been utilised already by the ancient astronomers like Ptolemy
Claudius Ptolemy (; , ; ; – 160s/170s AD) was a Greco-Roman mathematician, astronomer, astrologer, geographer, and music theorist who wrote about a dozen scientific treatises, three of which were important to later Byzantine science, Byzant ...
.
François d'Aguilon gave the stereographic projection its current name in his 1613 work ''Opticorum libri sex philosophis juxta ac mathematicis utiles'' (Six Books of Optics, useful for philosophers and mathematicians alike).
In the late 16th century, Thomas Harriot proved that the stereographic projection is conformal; however, this proof was never published and sat among his papers in a box for more than three centuries. In 1695, Edmond Halley
Edmond (or Edmund) Halley (; – ) was an English astronomer, mathematician and physicist. He was the second Astronomer Royal in Britain, succeeding John Flamsteed in 1720.
From an observatory he constructed on Saint Helena in 1676–77, Hal ...
, motivated by his interest in star charts, was the first to publish a proof. He used the recently established tools of calculus
Calculus is the mathematics, mathematical study of continuous change, in the same way that geometry is the study of shape, and algebra is the study of generalizations of arithmetic operations.
Originally called infinitesimal calculus or "the ...
, invented by his friend Isaac Newton
Sir Isaac Newton () was an English polymath active as a mathematician, physicist, astronomer, alchemist, theologian, and author. Newton was a key figure in the Scientific Revolution and the Age of Enlightenment, Enlightenment that followed ...
.
Definition
First formulation
Theunit sphere
In mathematics, a unit sphere is a sphere of unit radius: the locus (mathematics), set of points at Euclidean distance 1 from some center (geometry), center point in three-dimensional space. More generally, the ''unit -sphere'' is an n-sphere, -s ...
in three-dimensional space is the set of points such that . Let be the "north pole", and let be the rest of the sphere. The plane runs through the center of the sphere; the "equator" is the intersection of the sphere with this plane.
For any point on , there is a unique line through and , and this line intersects the plane in exactly one point , known as the stereographic projection of onto the plane.
In Cartesian coordinates
In geometry, a Cartesian coordinate system (, ) in a plane is a coordinate system that specifies each point uniquely by a pair of real numbers called ''coordinates'', which are the signed distances to the point from two fixed perpendicular o ...
on the sphere and on the plane, the projection and its inverse are given by the formulas
:
In spherical coordinates on the sphere (with the zenith angle, , and the azimuth
An azimuth (; from ) is the horizontal angle from a cardinal direction, most commonly north, in a local or observer-centric spherical coordinate system.
Mathematically, the relative position vector from an observer ( origin) to a point ...
, ) and polar coordinates
In mathematics, the polar coordinate system specifies a given point (mathematics), point in a plane (mathematics), plane by using a distance and an angle as its two coordinate system, coordinates. These are
*the point's distance from a reference ...
on the plane, the projection and its inverse are
:
Here, is understood to have value when . Also, there are many ways to rewrite these formulas using trigonometric identities. In cylindrical coordinates on the sphere and polar coordinates on the plane, the projection and its inverse are
:
Other conventions
Some authors define stereographic projection from the north pole (0, 0, 1) onto the plane , which is tangent to the unit sphere at the south pole (0, 0, −1). This can be described as a composition of a projection onto the equatorial plane described above, and a homothety from it to the polar plane. The homothety scales the image by a factor of 2 (a ratio of a diameter to a radius of the sphere), hence the values and produced by this projection are exactly twice those produced by the equatorial projection described in the preceding section. For example, this projection sends the equator to the circle of radius 2 centered at the origin. While the equatorial projection produces no infinitesimal area distortion along the equator, this pole-tangent projection instead produces no infinitesimal area distortion at the south pole. Other authors use a sphere of radius and the plane . In this case the formulae become : In general, one can define a stereographic projection from any point on the sphere onto any plane such that * is perpendicular to the diameter through , and * does not contain . As long as meets these conditions, then for any point other than the line through and meets in exactly one point , which is defined to be the stereographic projection of ''P'' onto ''E''.Generalizations
More generally, stereographic projection may be applied to the unit -sphere in ()-dimensionalEuclidean space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are ''Euclidean spaces ...
. If is a point of and a hyperplane
In geometry, a hyperplane is a generalization of a two-dimensional plane in three-dimensional space to mathematical spaces of arbitrary dimension. Like a plane in space, a hyperplane is a flat hypersurface, a subspace whose dimension is ...
in , then the stereographic projection of a point is the point of intersection of the line with . In Cartesian coordinates
In geometry, a Cartesian coordinate system (, ) in a plane is a coordinate system that specifies each point uniquely by a pair of real numbers called ''coordinates'', which are the signed distances to the point from two fixed perpendicular o ...
(, from 0 to ) on and (, from 1 to ''n'') on , the projection from is given by
Defining
the inverse is given by
Still more generally, suppose that is a (nonsingular) quadric hypersurface in the projective space . In other words, is the locus of zeros of a non-singular quadratic form in the homogeneous coordinates . Fix any point on and a hyperplane in not containing . Then the stereographic projection of a point in is the unique point of intersection of with . As before, the stereographic projection is conformal and invertible on a non-empty Zariski open set. The stereographic projection presents the quadric hypersurface as a rational hypersurface. This construction plays a role in algebraic geometry
Algebraic geometry is a branch of mathematics which uses abstract algebraic techniques, mainly from commutative algebra, to solve geometry, geometrical problems. Classically, it studies zero of a function, zeros of multivariate polynomials; th ...
and conformal geometry.
Properties
The first stereographic projection defined in the preceding section sends the "south pole" (0, 0, −1) of theunit sphere
In mathematics, a unit sphere is a sphere of unit radius: the locus (mathematics), set of points at Euclidean distance 1 from some center (geometry), center point in three-dimensional space. More generally, the ''unit -sphere'' is an n-sphere, -s ...
to (0, 0), the equator to the unit circle
In mathematics, a unit circle is a circle of unit radius—that is, a radius of 1. Frequently, especially in trigonometry, the unit circle is the circle of radius 1 centered at the origin (0, 0) in the Cartesian coordinate system in the Eucli ...
, the southern hemisphere to the region inside the circle, and the northern hemisphere to the region outside the circle.
The projection is not defined at the projection point = (0, 0, 1). Small neighborhoods of this point are sent to subsets of the plane far away from (0, 0). The closer is to (0, 0, 1), the more distant its image is from (0, 0) in the plane. For this reason it is common to speak of (0, 0, 1) as mapping to "infinity" in the plane, and of the sphere as completing the plane by adding a point at infinity. This notion finds utility in projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant with respect to projective transformations. This means that, compared to elementary Euclidean geometry, projective geometry has a different setting (''p ...
and complex analysis. On a merely topological level, it illustrates how the sphere is homeomorphic
In mathematics and more specifically in topology, a homeomorphism ( from Greek roots meaning "similar shape", named by Henri Poincaré), also called topological isomorphism, or bicontinuous function, is a bijective and continuous function betw ...
to the one-point compactification of the plane.
In Cartesian coordinates
In geometry, a Cartesian coordinate system (, ) in a plane is a coordinate system that specifies each point uniquely by a pair of real numbers called ''coordinates'', which are the signed distances to the point from two fixed perpendicular o ...
a point on the sphere and its image on the plane either both are rational point
In number theory and algebraic geometry, a rational point of an algebraic variety is a point whose coordinates belong to a given field. If the field is not mentioned, the field of rational numbers is generally understood. If the field is the fiel ...
s or none of them:
:
Stereographic projection is conformal, meaning that it preserves the angles at which curves cross each other (see figures). On the other hand, stereographic projection does not preserve area; in general, the area of a region of the sphere does not equal the area of its projection onto the plane. The area element is given in coordinates by
:
Along the unit circle, where , there is no inflation of area in the limit, giving a scale factor of 1. Near (0, 0) areas are inflated by a factor of 4, and near infinity areas are inflated by arbitrarily small factors.
The metric is given in coordinates by
:
and is the unique formula found in Bernhard Riemann
Georg Friedrich Bernhard Riemann (; ; 17September 182620July 1866) was a German mathematician who made profound contributions to analysis, number theory, and differential geometry. In the field of real analysis, he is mostly known for the f ...
's ''Habilitationsschrift'' on the foundations of geometry, delivered at Göttingen in 1854, and entitled ''Über die Hypothesen welche der Geometrie zu Grunde liegen''.
No map from the sphere to the plane can be both conformal and area-preserving. If it were, then it would be a local isometry and would preserve Gaussian curvature
In differential geometry, the Gaussian curvature or Gauss curvature of a smooth Surface (topology), surface in three-dimensional space at a point is the product of the principal curvatures, and , at the given point:
K = \kappa_1 \kappa_2.
For ...
. The sphere and the plane have different Gaussian curvatures, so this is impossible.
Circles on the sphere that do ''not'' pass through the point of projection are projected to circles on the plane. Circles on the sphere that ''do'' pass through the point of projection are projected to straight lines on the plane. These lines are sometimes thought of as circles through the point at infinity, or circles of infinite radius. These properties can be verified by using the expressions of in terms of given in : using these expressions for a substitution in the equation of the plane containing a circle on the sphere, and clearing denominators, one gets the equation of a circle, that is, a second-degree equation with as its quadratic part. The equation becomes linear if that is, if the plane passes through the point of projection.
All lines in the plane, when transformed to circles on the sphere by the inverse of stereographic projection, meet at the projection point. Parallel lines, which do not intersect in the plane, are transformed to circles tangent at projection point. Intersecting lines are transformed to circles that intersect transversally at two points in the sphere, one of which is the projection point. (Similar remarks hold about the real projective plane, but the intersection relationships are different there.)
The loxodromes of the sphere map to curves on the plane of the form
:
where the parameter measures the "tightness" of the loxodrome. Thus loxodromes correspond to logarithmic spiral
A logarithmic spiral, equiangular spiral, or growth spiral is a self-similarity, self-similar spiral curve that often appears in nature. The first to describe a logarithmic spiral was Albrecht Dürer (1525) who called it an "eternal line" ("ewi ...
s. These spirals intersect radial lines in the plane at equal angles, just as the loxodromes intersect meridians on the sphere at equal angles.
 The stereographic projection relates to the plane inversion in a simple way. Let and be two points on the sphere with projections and on the plane. Then and are inversive images of each other in the image of the equatorial circle if and only if and are reflections of each other in the equatorial plane.
In other words, if:
* is a point on the sphere, but not a 'north pole' and not its antipode, the 'south pole' ,
* is the image of in a stereographic projection with the projection point and
* is the image of in a stereographic projection with the projection point ,
then and are inversive images of each other in the unit circle.
:
The stereographic projection relates to the plane inversion in a simple way. Let and be two points on the sphere with projections and on the plane. Then and are inversive images of each other in the image of the equatorial circle if and only if and are reflections of each other in the equatorial plane.
In other words, if:
* is a point on the sphere, but not a 'north pole' and not its antipode, the 'south pole' ,
* is the image of in a stereographic projection with the projection point and
* is the image of in a stereographic projection with the projection point ,
then and are inversive images of each other in the unit circle.
:
Wulff net
equator
The equator is the circle of latitude that divides Earth into the Northern Hemisphere, Northern and Southern Hemisphere, Southern Hemispheres of Earth, hemispheres. It is an imaginary line located at 0 degrees latitude, about in circumferen ...
(such as the Eastern or Western hemisphere of a planet).
In the figure, the area-distorting property of the stereographic projection can be seen by comparing a grid sector near the center of the net with one at the far right or left. The two sectors have equal areas on the sphere. On the disk, the latter has nearly four times the area of the former. If the grid is made finer, this ratio approaches exactly 4.
On the Wulff net, the images of the parallels and meridians intersect at right angles. This orthogonality property is a consequence of the angle-preserving property of the stereographic projection. (However, the angle-preserving property is stronger than this property. Not all projections that preserve the orthogonality of parallels and meridians are angle-preserving.)
For an example of the use of the Wulff net, imagine two copies of it on thin paper, one atop the other, aligned and tacked at their mutual center. Let be the point on the lower unit hemisphere whose spherical coordinates are (140°, 60°) and whose Cartesian coordinates are (0.321, 0.557, −0.766). This point lies on a line oriented 60° counterclockwise from the positive -axis (or 30° clockwise from the positive -axis) and 50° below the horizontal plane . Once these angles are known, there are four steps to plotting :
#Using the grid lines, which are spaced 10° apart in the figures here, mark the point on the edge of the net that is 60° counterclockwise from the point (1, 0) (or 30° clockwise from the point (0, 1)).
#Rotate the top net until this point is aligned with (1, 0) on the bottom net.
#Using the grid lines on the bottom net, mark the point that is 50° toward the center from that point.
#Rotate the top net oppositely to how it was oriented before, to bring it back into alignment with the bottom net. The point marked in step 3 is then the projection that we wanted.
To plot other points, whose angles are not such round numbers as 60° and 50°, one must visually interpolate between the nearest grid lines. It is helpful to have a net with finer spacing than 10°. Spacings of 2° are common.
To find the central angle between two points on the sphere based on their stereographic plot, overlay the plot on a Wulff net and rotate the plot about the center until the two points lie on or near a meridian. Then measure the angle between them by counting grid lines along that meridian.
Applications within mathematics
Complex analysis
manifold
In mathematics, a manifold is a topological space that locally resembles Euclidean space near each point. More precisely, an n-dimensional manifold, or ''n-manifold'' for short, is a topological space with the property that each point has a N ...
).
This construction has special significance in complex analysis. The point in the real plane can be identified with the complex number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the for ...
. The stereographic projection from the north pole onto the equatorial plane is then
:
Similarly, letting be another complex coordinate, the functions
:
define a stereographic projection from the south pole onto the equatorial plane. The transition maps between the - and -coordinates are then and , with approaching 0 as goes to infinity, and ''vice versa''. This facilitates an elegant and useful notion of infinity for the complex numbers and indeed an entire theory of meromorphic functions mapping to the Riemann sphere. The standard metric on the unit sphere agrees with the Fubini–Study metric on the Riemann sphere.
Visualization of lines and planes
The set of all lines through the origin in three-dimensional space forms a space called the real projective plane. This plane is difficult to visualize, because it cannot be embedded in three-dimensional space. However, one can visualize it as a disk, as follows. Any line through the origin intersects the southern hemisphere ≤ 0 in a point, which can then be stereographically projected to a point on a disk in the XY plane. Horizontal lines through the origin intersect the southern hemisphere in two antipodal points along the equator, which project to the boundary of the disk. Either of the two projected points can be considered part of the disk; it is understood that antipodal points on the equator represent a single line in 3 space and a single point on the boundary of the projected disk (see quotient topology). So any set of lines through the origin can be pictured as a set of points in the projected disk. But the boundary points behave differently from the boundary points of an ordinary 2-dimensional disk, in that any one of them is simultaneously close to interior points on opposite sides of the disk (just as two nearly horizontal lines through the origin can project to points on opposite sides of the disk). Also, every plane through the origin intersects the unit sphere in a great circle, called the ''trace'' of the plane. This circle maps to a circle under stereographic projection. So the projection lets us visualize planes as circular arcs in the disk. Prior to the availability of computers, stereographic projections with great circles often involved drawing large-radius arcs that required use of a beam compass. Computers now make this task much easier. Further associated with each plane is a unique line, called the plane's ''pole'', that passes through the origin and is perpendicular to the plane. This line can be plotted as a point on the disk just as any line through the origin can. So the stereographic projection also lets us visualize planes as points in the disk. For plots involving many planes, plotting their poles produces a less-cluttered picture than plotting their traces. This construction is used to visualize directional data in crystallography and geology, as described below.Other visualization
Stereographic projection is also applied to the visualization of polytopes. In aSchlegel diagram
In geometry, a Schlegel diagram is a projection of a polytope from \mathbb^d into \mathbb^ through a point just outside one of its facets. The resulting entity is a polytopal subdivision of the facet in \mathbb^ that, together with the ori ...
, an -dimensional polytope in is projected onto an -dimensional sphere, which is then stereographically projected onto . The reduction from to can make the polytope easier to visualize and understand.
Arithmetic geometry
In elementary arithmetic geometry, stereographic projection from the unit circle provides a means to describe all primitivePythagorean triple
A Pythagorean triple consists of three positive integers , , and , such that . Such a triple is commonly written , a well-known example is . If is a Pythagorean triple, then so is for any positive integer . A triangle whose side lengths are a Py ...
s. Specifically, stereographic projection from the north pole (0,1) onto the -axis gives a one-to-one correspondence between the rational number
In mathematics, a rational number is a number that can be expressed as the quotient or fraction of two integers, a numerator and a non-zero denominator . For example, is a rational number, as is every integer (for example,
The set of all ...
points on the unit circle (with ) and the rational point
In number theory and algebraic geometry, a rational point of an algebraic variety is a point whose coordinates belong to a given field. If the field is not mentioned, the field of rational numbers is generally understood. If the field is the fiel ...
s of the -axis. If is a rational point on the -axis, then its inverse stereographic projection is the point
:
which gives Euclid's formula for a Pythagorean triple.
Tangent half-angle substitution
integral
In mathematics, an integral is the continuous analog of a Summation, sum, which is used to calculate area, areas, volume, volumes, and their generalizations. Integration, the process of computing an integral, is one of the two fundamental oper ...
s involving trigonometric functions.
Applications to other disciplines
Cartography
The fundamental problem of cartography is that no map from the sphere to the plane can accurately represent both angles and areas. In general, area-preserving map projections are preferred forstatistical
Statistics (from German language, German: ', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a s ...
applications, while angle-preserving (conformal) map projections are preferred for navigation
Navigation is a field of study that focuses on the process of monitoring and controlling the motion, movement of a craft or vehicle from one place to another.Bowditch, 2003:799. The field of navigation includes four general categories: land navig ...
.
Stereographic projection falls into the second category. When the projection is centered at the Earth's north or south pole, it has additional desirable properties: It sends meridians to rays emanating from the origin and parallels to circles centered at the origin.
Tissot's indicatrix
In cartography, a Tissot's indicatrix (Tissot indicatrix, Tissot's ellipse, Tissot ellipse, ellipse of distortion) (plural: "Tissot's indicatrices") is a mathematical contrivance presented by French mathematician Nicolas Auguste Tissot in 1859 ...
of deformation.
Planetary science
The stereographic is the only projection that maps all circles on a sphere to circles on a plane. This property is valuable in planetary mapping where craters are typical features. The set of circles passing through the point of projection have unbounded radius, and therefore degenerate into lines.Crystallography
Incrystallography
Crystallography is the branch of science devoted to the study of molecular and crystalline structure and properties. The word ''crystallography'' is derived from the Ancient Greek word (; "clear ice, rock-crystal"), and (; "to write"). In J ...
, the orientations of crystal
A crystal or crystalline solid is a solid material whose constituents (such as atoms, molecules, or ions) are arranged in a highly ordered microscopic structure, forming a crystal lattice that extends in all directions. In addition, macros ...
axes and faces in three-dimensional space are a central geometric concern, for example in the interpretation of X-ray
An X-ray (also known in many languages as Röntgen radiation) is a form of high-energy electromagnetic radiation with a wavelength shorter than those of ultraviolet rays and longer than those of gamma rays. Roughly, X-rays have a wavelength ran ...
and electron diffraction patterns. These orientations can be visualized as in the section Visualization of lines and planes above. That is, crystal axes and poles to crystal planes are intersected with the northern hemisphere and then plotted using stereographic projection. A plot of poles is called a pole figure.
In electron diffraction, Kikuchi line pairs appear as bands decorating the intersection between lattice plane traces and the Ewald sphere thus providing ''experimental access'' to a crystal's stereographic projection. Model Kikuchi maps in reciprocal space, and fringe visibility maps for use with bend contours in direct space, thus act as road maps for exploring orientation space with crystals in the transmission electron microscope
Transmission electron microscopy (TEM) is a microscopy technique in which a beam of electrons is transmitted through a specimen to form an image. The specimen is most often an ultrathin section less than 100 nm thick or a suspension on a gr ...
.
Geology
 Researchers in
Researchers in structural geology
Structural geology is the study of the three-dimensional distribution of rock units with respect to their deformational histories. The primary goal of structural geology is to use measurements of present-day rock geometries to uncover informati ...
are concerned with the orientations of planes and lines for a number of reasons. The foliation
In mathematics (differential geometry), a foliation is an equivalence relation on an topological manifold, ''n''-manifold, the equivalence classes being connected, injective function, injectively immersed submanifolds, all of the same dimension ...
of a rock is a planar feature that often contains a linear feature called lineation. Similarly, a fault plane is a planar feature that may contain linear features such as slickensides.
These orientations of lines and planes at various scales can be plotted using the methods of the Visualization of lines and planes section above. As in crystallography, planes are typically plotted by their poles. Unlike crystallography, the southern hemisphere is used instead of the northern one (because the geological features in question lie below the Earth's surface). In this context the stereographic projection is often referred to as the equal-angle lower-hemisphere projection. The equal-area lower-hemisphere projection defined by the Lambert azimuthal equal-area projection is also used, especially when the plot is to be subjected to subsequent statistical analysis such as density contouring.
Rock mechanics
The stereographic projection is one of the most widely used methods for evaluating rock slope stability. It allows for the representation and analysis of three-dimensional orientation data in two dimensions. Kinematic analysis within stereographic projection is used to assess the potential for various modes of rock slope failures—such as plane, wedge, and toppling failures—which occur due to the presence of unfavorably oriented discontinuities. This technique is particularly useful for visualizing the orientation of rock slopes in relation to discontinuity sets, facilitating the assessment of the most likely failure type. For instance, plane failure is more likely when the strike of a discontinuity set is parallel to the slope, and the discontinuities dip towards the slope at an angle steep enough to allow sliding, but not steeper than the slope itself. Additionally, some authors have developed graphical methods based on stereographic projection to easily calculate geometrical correction parameters—such as those related to the parallelism between the slope and discontinuities, the dip of the discontinuity, and the relative angle between the discontinuity and the slope—for rock mass classifications in slopes, including slope mass rating (SMR) and rock mass rating.Photography
 Some
Some fisheye lens
A fisheye lens is an ultra wide angle lens, ultra wide-angle lens that produces strong Distortion (optics), visual distortion intended to create a wide panorama, panoramic or Sphere#Hemisphere, hemispherical image. Fisheye lenses achieve extremel ...
es use a stereographic projection to capture a wide-angle view. Compared to more traditional fisheye lenses which use an equal-area projection, areas close to the edge retain their shape, and straight lines are less curved. However, stereographic fisheye lenses are typically more expensive to manufacture. Image remapping software, such as Panotools, allows the automatic remapping of photos from an equal-area fisheye to a stereographic projection.
The stereographic projection has been used to map spherical panoramas, starting with Horace Bénédict de Saussure's in 1779. This results in effects known as a ''little planet'' (when the center of projection is the nadir
The nadir is the direction pointing directly ''below'' a particular location; that is, it is one of two vertical directions at a specified location, orthogonal to a horizontal flat surface.
The direction opposite of the nadir is the zenith.
Et ...
) and a ''tube'' (when the center of projection is the zenith
The zenith (, ) is the imaginary point on the celestial sphere directly "above" a particular location. "Above" means in the vertical direction (Vertical and horizontal, plumb line) opposite to the gravity direction at that location (nadir). The z ...
).German ''et al.'' (2007).
The popularity of using stereographic projections to map panoramas over other azimuthal projections is attributed to the shape preservation that results from the conformality of the projection.
See also
* List of map projections *Astrolabe
An astrolabe (; ; ) is an astronomy, astronomical list of astronomical instruments, instrument dating to ancient times. It serves as a star chart and Model#Physical model, physical model of the visible celestial sphere, half-dome of the sky. It ...
* Astronomical clock
*Poincaré disk model
In geometry, the Poincaré disk model, also called the conformal disk model, is a model of 2-dimensional hyperbolic geometry in which all points are inside the unit disk, and straight lines are either circular arcs contained within the disk t ...
, the analogous mapping of the hyperbolic plane
* Stereographic projection in cartography
* Curvilinear perspective
*Fisheye lens
A fisheye lens is an ultra wide angle lens, ultra wide-angle lens that produces strong Distortion (optics), visual distortion intended to create a wide panorama, panoramic or Sphere#Hemisphere, hemispherical image. Fisheye lenses achieve extremel ...
References
Sources
* * * * * * * * * * * * * *External links
Stereographic Projection and Inversion
from
Cut-the-Knot
Alexander Bogomolny (January 4, 1948 July 7, 2018) was a Soviet Union, Soviet-born Israeli Americans, Israeli-American mathematician. He was Professor Emeritus of Mathematics at the University of Iowa, and formerly research fellow at the Moscow ...
DoITPoMS Teaching and Learning Package - "The Stereographic Projection"
Videos
Proof about Stereographic Projection taking circles in the sphere to circles in the plane
*
Software
Stereonet
a software tool for structural geology by Rick Allmendinger.
PTCLab
the phase transformation crystallography lab
Sphaerica
software tool for straightedge and compass construction on the sphere, including a stereographic projection display option
Estereografica Web
a web application for stereographic projection in structural geology and fault kinematics by Ernesto Cristallini. {{Authority control Conformal mappings Conformal projections Crystallography Projective geometry