Squigonometry on:
[Wikipedia]
[Google]
[Amazon]
Squigonometry or -trigonometry is a generalization of traditional
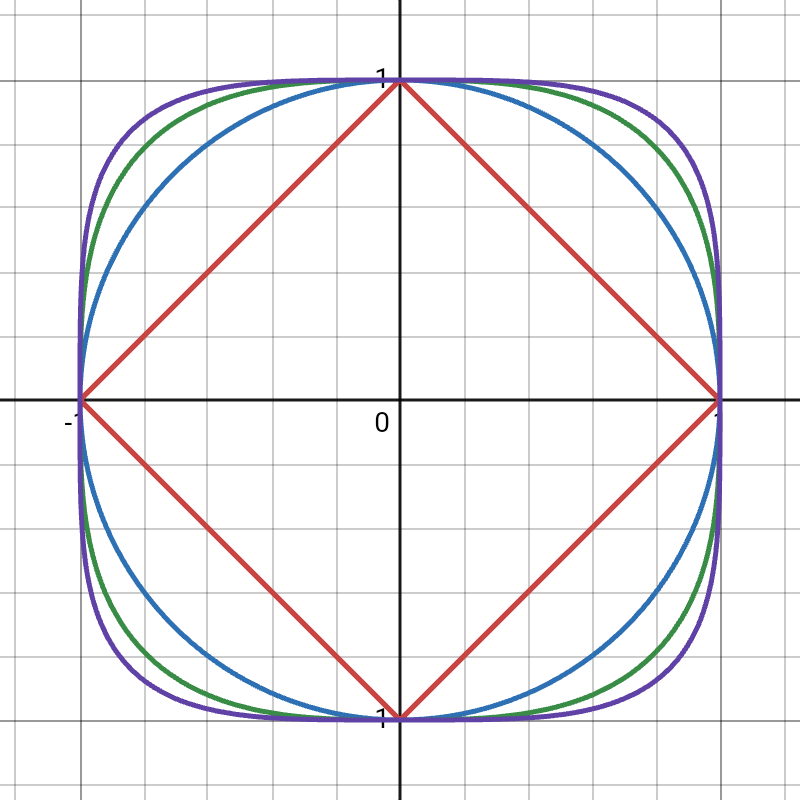 The cosquine and squine functions, denoted as and can be defined analogously to trigonometric functions on a
The cosquine and squine functions, denoted as and can be defined analogously to trigonometric functions on a
trigonometry
Trigonometry () is a branch of mathematics concerned with relationships between angles and side lengths of triangles. In particular, the trigonometric functions relate the angles of a right triangle with ratios of its side lengths. The fiel ...
which replaces the circle
A circle is a shape consisting of all point (geometry), points in a plane (mathematics), plane that are at a given distance from a given point, the Centre (geometry), centre. The distance between any point of the circle and the centre is cal ...
and Euclidean distance
In mathematics, the Euclidean distance between two points in Euclidean space is the length of the line segment between them. It can be calculated from the Cartesian coordinates of the points using the Pythagorean theorem, and therefore is o ...
function with the squircle
A squircle is a shape intermediate between a square and a circle. There are at least two definitions of "squircle" in use, one based on the superellipse, the other arising from work in optics. The word "squircle" is a portmanteau of the words " ...
(shape intermediate between a square
In geometry, a square is a regular polygon, regular quadrilateral. It has four straight sides of equal length and four equal angles. Squares are special cases of rectangles, which have four equal angles, and of rhombuses, which have four equal si ...
and circle) and -norm. While trigonometry deals with the relationships between angle
In Euclidean geometry, an angle can refer to a number of concepts relating to the intersection of two straight Line (geometry), lines at a Point (geometry), point. Formally, an angle is a figure lying in a Euclidean plane, plane formed by two R ...
s and lengths in the plane using trigonometric functions
In mathematics, the trigonometric functions (also called circular functions, angle functions or goniometric functions) are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in all ...
defined relative to a unit circle
In mathematics, a unit circle is a circle of unit radius—that is, a radius of 1. Frequently, especially in trigonometry, the unit circle is the circle of radius 1 centered at the origin (0, 0) in the Cartesian coordinate system in the Eucli ...
, squigonometry focuses on analogous relationships and functions within the context of a unit squircle.
Etymology
The term squigonometry is aportmanteau
In linguistics, a blend—also known as a blend word, lexical blend, or portmanteau—is a word formed by combining the meanings, and parts of the sounds, of two or more words together.
of ''square'' or ''squircle'' and ''trigonometry''. It was used by Derek Holton to refer to an analog of trigonometry using a square as a basic shape (instead of a circle) in his 1990 pamphlet ''Creating Problems''. In 2011 it was used by William Wood to refer to trigonometry with a squircle as its base shape in a recreational mathematics article in ''Mathematics Magazine
''Mathematics Magazine'' is a refereed bimonthly publication of the Mathematical Association of America. Its intended audience is teachers of collegiate mathematics, especially at the junior/senior level, and their students. It is explicitly a j ...
''. In 2016 Robert Poodiack extended Wood's work in another ''Mathematics Magazine'' article. Wood and Poodiack published a book about the topic in 2022.
However, the idea of generalizing trigonometry to curves other than circles is centuries older.
Squigonometric functions
Cosquine and squine
Definition through unit squircle
 The cosquine and squine functions, denoted as and can be defined analogously to trigonometric functions on a
The cosquine and squine functions, denoted as and can be defined analogously to trigonometric functions on a unit circle
In mathematics, a unit circle is a circle of unit radius—that is, a radius of 1. Frequently, especially in trigonometry, the unit circle is the circle of radius 1 centered at the origin (0, 0) in the Cartesian coordinate system in the Eucli ...
, but instead using the coordinates
In geometry, a coordinate system is a system that uses one or more numbers, or coordinates, to uniquely determine and standardize the Position (geometry), position of the Point (geometry), points or other geometric elements on a manifold such as ...
of points on a ''unit squircle'', described by the equation
In mathematics, an equation is a mathematical formula that expresses the equality of two expressions, by connecting them with the equals sign . The word ''equation'' and its cognates in other languages may have subtly different meanings; for ...
:
:
where is a real number
In mathematics, a real number is a number that can be used to measure a continuous one- dimensional quantity such as a duration or temperature. Here, ''continuous'' means that pairs of values can have arbitrarily small differences. Every re ...
greater than or equal to 1. Here corresponds to and corresponds to
Notably, when , the squigonometric functions coincide with the trigonometric functions.
Definition through differential equations
Similarly to how trigonometric functions are defined through differential equations, the cosquine and squine functions are also uniquely determined by solving the coupledinitial value problem
In multivariable calculus, an initial value problem (IVP) is an ordinary differential equation together with an initial condition which specifies the value of the unknown function at a given point in the domain. Modeling a system in physics or ...
:
Where corresponds to and corresponds to .
Definition through
analysis
Analysis (: analyses) is the process of breaking a complex topic or substance into smaller parts in order to gain a better understanding of it. The technique has been applied in the study of mathematics and logic since before Aristotle (38 ...
The definition of sine and cosine through integrals can be extended to define the squigonometric functions. Let