Squeezed Light

In quantum physics, light is in a '' squeezed state'' if its electric field strength ''Ԑ'' for some phases $\vartheta$ has a quantum uncertainty smaller than that of a coherent state. The term ''squeezing'' thus refers to a reduced quantum uncertainty. To obey Heisenberg's uncertainty relation, a squeezed state must also have phases at which the electric field uncertainty is ''anti-squeezed'', i.e. larger than that of a coherent state. Since 2019, the gravitational-wave observatories LIGO and Virgo employ ''squeezed'' laser light, which has significantly increased the rate of observed gravitational-wave events.

Quantum physical background

An oscillating physical quantity cannot have precisely defined values at all phases of the oscillation. This is true for the electric and magnetic fields of an electromagnetic wave, as well as for any other wave or oscillation (see figure right). This fact can be observed in experiments and is described by quantum theory. For electromagnetic waves usually just the electric field is considered, because it is the one that mainly interacts with matter.

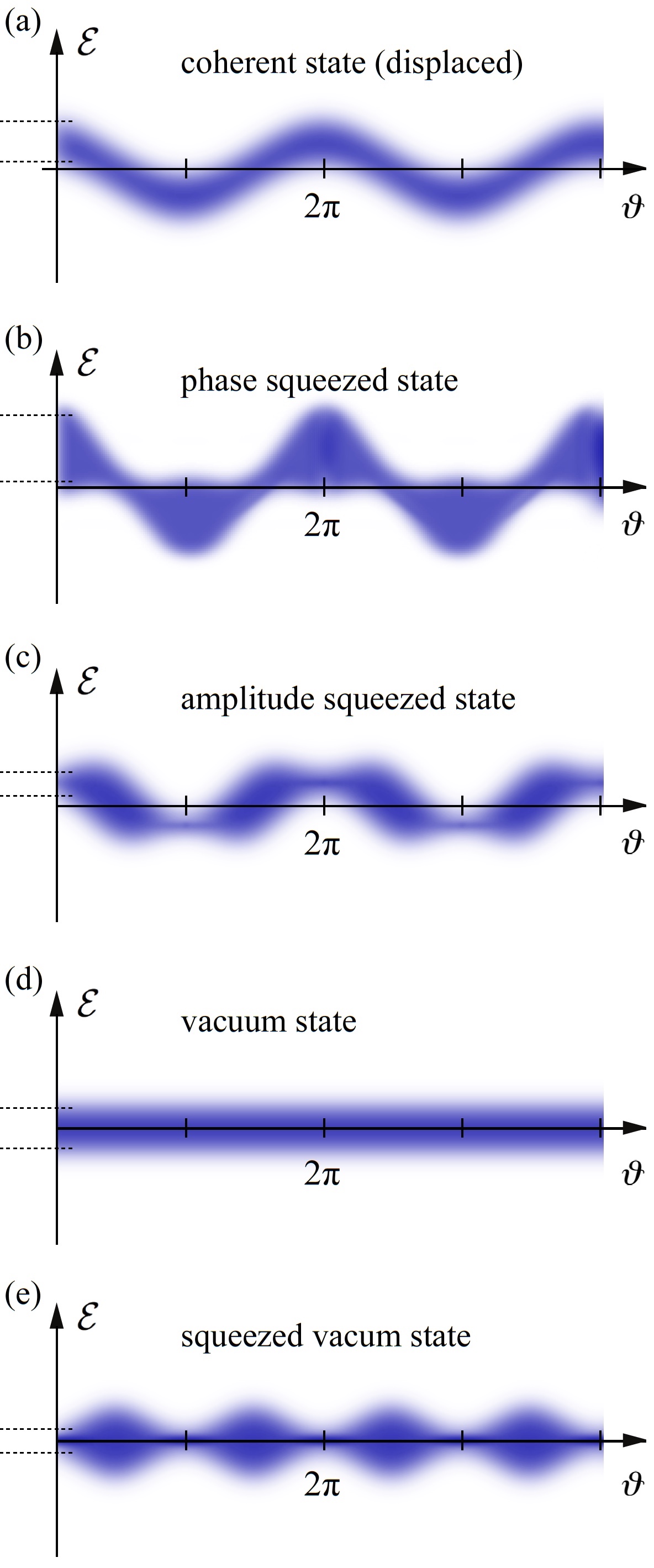
Fig. 1. shows five different quantum states that a monochromatic wave could be in. The difference of the five quantum states is given by different electric field excitations and by different distributions of the quantum uncertainty along the phase $\vartheta$. For a ''displaced coherent state'', the expectation (mean) value of the electric field shows an oscillation, with an uncertainty independent of the phase (a). Also the ''phase''- (b) and ''amplitude-squeezed states'' (c) show an oscillation of the mean electric field, but here the uncertainty depends on phase and is ''squeezed'' for some phases. The vacuum state (d) is a special coherent state and is not squeezed. It has zero mean electric field for all phases and a phase-independent uncertainty. It has zero energy on average, i.e. zero photons, and is the ground state of the monochromatic wave we consider. Finally, a ''squeezed vacuum state'' has also a zero mean electric field but a ''phase-dependent'' uncertainty (e).

Generally, ''quantum uncertainty'' reveals itself through a large number of ''identical'' measurements on ''identical'' quantum objects (here: modes of light) that, however, give ''different'' results. Let us again consider a continuous-wave monochromatic light wave (as emitted by an ultra-stable laser). A single measurement of ''Ԑ''$(\vartheta_1)$ is performed over many periods of the light wave and provides a single number. The next measurements of ''Ԑ''$(\vartheta_1)$ will be done consecutively on the same laser beam. Having recorded a large number of such measurements we know the field uncertainty at $\vartheta_1$. In order to get the ''full'' picture, and for instance Fig.1(b), we need to record the statistics at many different phases $0<\vartheta_i<\pi$.

Quantitative description of (squeezed) uncertainty

The measured electric field strengths at the wave's phase $\vartheta$ are the eigenvalues of the normalized quadrature operator $X_\vartheta$, defined as
: \hat_\vartheta = \frac \left ^ \hat + e^ \hat^\dagger \right= \cos(\vartheta)\, \hat + \sin(\vartheta)\, \hat
where $\hat$ and $\hat^\dagger$ are the annihilation and creation operators, respectively, of the oscillator representing the photon.
$X_ \equiv X$ is the wave's ''amplitude quadrature'', equivalent to the position in optical phase space, and $X_ \equiv Y$ is the wave's ''phase quadrature'', equivalent to momentum. $X$ and $Y$ are non-commuting observables. Although they represent electric fields, they are dimensionless and satisfy the following uncertainty relation:
: $\;\Delta X^2 \Delta Y^2 \geq \frac$ ,
where $\Delta^2$ stands for the v''ariance''. (The variance is the mean of the squares of the measuring values minus the square of the mean of the measuring values.) If a mode of light is in its ground state $, 0\rangle$ (having an average photon number of zero), the uncertainty relation above is saturated and the variances of the quadrature are $\Delta X^2_g = \Delta Y^2_g = 1/4$. (Other normalizations can also be found in literature. The normalization chosen here has the nice property that the sum of the ground state variances directly provide the zero point excitation of the quantized harmonic oscillator $\Delta^2 X_g + \Delta^2 Y_g = 1/2$).

:Definition: Light is in a squeezed state, if (and only if) a phase $\vartheta$ exists for which $\;\Delta^2 X_\vartheta < \Delta^2 X_g = \frac4$.

While coherent states belong to the ''semi-classical'' states, since they can be fully described by a semi-classical model, squeezed states of light belong to the so-called ''nonclassical'' states, which also include number states (Fock states) and Schrödinger cat states.

Squeezed states (of light) were first produced in the mid 1980s.R. E. Slusher et al., ''Observation of squeezed states generated by four wave mixing in an optical cavity'', Phys. Rev. Lett. 55 (22), 2409 (1985)
At that time, quantum noise squeezing by up to a factor of about 2 (3 dB) in variance was achieved, i.e. $\Delta^2 X_\vartheta \approx \Delta^2 X_g/2$. Today, squeeze factors larger than 10 (10 dB) have been directly observed. A limitation is set by decoherence, mainly in terms of optical loss.

The ''squeeze factor'' in Decibel (dB) can be computed in the following way:
: $-10 \cdot \log \frac$, where $\Delta^2_\mathrm X_\vartheta$ is the smallest variance when varying the phase $\vartheta$ from 0 to $\pi$. This particular phase $\vartheta$ is called the ''squeeze angle''.

Representation of squeezed states by quasi-probability densities

Quantum states such as those in Fig. 1 (a) to (e) are often displayed as Wigner functions, which are quasi-probability density distributions. Two orthogonal quadratures, usually $X$and $Y$, span a phase space diagram, and the third axes provides the quasi probability of yielding a certain combination of ;Y/math>. Since $X$and $Y$are not precisely defined simultaneously, we cannot talk about a 'probability' as we do in classical physics but call it a 'quasi probability'. A Wigner function is reconstructed from time series of $X(t)$and $Y(t)$. The reconstruction is also called 'quantum tomographic reconstruction'. For squeezed states, the Wigner function has a Gaussian shape, with an elliptical contour line, see Fig.: 1(f).

Physical meaning of measurement quantity and measurement object

Quantum uncertainty becomes visible when ''identical'' measurements of the same quantity (observable) on ''identical'' objects (here: ''modes of light'') give different results ( eigen values). In case of a single freely propagating monochromatic laser beam, the individual measurements are performed on consecutive time intervals of identical length. One interval must last much longer than the light's period; otherwise the monochromatic property would be significantly disturbed. Such consecutive measurements correspond to a ''time series'' of fluctuating eigen values. Consider an example in which the amplitude quadrature $X$ was repeatedly measured. The time series can be used for a quantum statistical characterization of the modes of light.
Obviously, the amplitude of the light wave might be different before and after our measurement, i.e. the time series does not provide any information about very slow changes of the amplitude, which corresponds to very low frequencies. This is a trivial but also fundamental issue, since any data taking lasts for a finite time. Our time series, however, does provide meaningful information about fast changes of the light's amplitude, i.e. changes at frequencies higher than the inverse of the full measuring time. Changes that are faster than the duration of a ''single'' measurement, however, are invisible again. A quantum statistical characterization through ''consecutive'' measurements on some sort of a carrier is thus always related to a specific frequency interval, for instance described by $f \pm \Delta f/2$ with $f > \Delta f/2 >0.$ Based on this insight, we can describe the physical meaning of the observable $X_\vartheta$ more clearly:

The quantum statistical characterization using identical consecutive modes carried by a laser beam confers to the laser beam's electric field ''modulation'' ''within a frequency interval''. The actual observable needs to be labeled accordingly, for instance as $X_$. $X_$ is the ''amplitude'' (or ''depth'') of the amplitude modulation and $Y_$ the ''amplitude'' (or ''depth'') of the phase modulation in the respective frequency interval. This leads to the doggerel expressions '''amplitude quadrature amplitude''' and '''phase quadrature amplitude.

Within some limitations, for instance set by the speed of the electronics, $f$ and $\Delta f$ can be freely chosen in course of data acquisition and, in particular, data processing. This choice also defines the measurement ''object'', i.e. the ''mode'' that is characterized by the statistics of the eigen values of $X_$ and $Y_$. The measurement object thus is a ''modulation mode'' that is carried by the light beam. – In many experiments, one is interested in a continuous spectrum of many modulation modes carried by the same light beam. Fig. 2 shows the squeeze factors of many neighboring modulation modes versus $f$. The upper trace refers to the uncertainties of the same modes being in their vacuum states, which serves as the 0 dB reference.

The observables in squeezed light experiments correspond exactly to those being used in optical communication. Amplitude modulation (AM) and frequency modulation (FM) are the classical means to imprint information on a carrier field. (Frequency modulation is mathematically closely related to phase modulation). The observables $X_$ and $Y_$ also correspond to the measurement quantities in laser interferometers, such as in Sagnac interferometers measuring rotation changes and in Michelson interferometers observing gravitational waves. ''Squeezed states of light'' thus have ample applications in optical communication and optical measurements. The most prominent and important application is in gravitational-wave observatories. Arguably, it is the first end-user driven application of quantum correlations. Squeezed light originally was not planned to be implemented in either Advanced LIGO nor in Advanced Virgo, but now it contributes a significant factor towards the observatories design sensitivities and increases the rate of observed gravitational-wave events.

Applications

Optical high-precision measurements

Squeezed light is used to reduce the photon counting noise (shot noise) in optical high-precision measurements, most notably in laser interferometers. There are a large number of proof-of-principle experiments. Laser interferometers split a laser beam in two paths and overlap them again afterwards. If the relative optical path length changes, the interference changes, and the light power in the interferometer's output port as well. This light power is detected with a photo diode providing a continuous voltage signal. If for instance the position of one interferometer mirror vibrates and thereby causes an oscillating path length difference, the output light has an amplitude modulation of the same frequency. Independent of the existence of such a (classical) signal, a beam of light always carries at least the vacuum state uncertainty (see above). The (modulation) signal with respect to this uncertainty can be improved by using a higher light power inside the interferometer arms, since the signal increases with the light power. This is the reason (in fact the only one) why Michelson interferometers for the detection of gravitational waves use very high optical power. High light power, however, produces technical problems. Mirror surfaces absorb parts of the light, become warmer, get thermally deformed and reduce the interferometer's interference contrast. Furthermore, an excessive light power can excite unstable mechanical vibrations of the mirrors. These consequences are mitigated if squeezed states of light are used for improving the signal-to-noise-ratio. Squeezed states of light do not increase the light's power. They also do not increase the signal, but instead reduce the noise.

Laser interferometers are usually operated with monochromatic continuous-wave light. The optimal signal-to-noise-ratio is achieved by either operating the differential interferometer arm lengths such that both output ports contain half of the input light power (half fringe) and by recording the difference signal from both ports, or by operating the interferometer close to a dark fringe for one of the output ports where just a single photodiode is placed. The latter operation point is used in gravitational-wave (GW) detectors.

For improving an interferometer sensitivity with squeezed states of light, the already existing bright light does not need to be fully replaced. What has to be replaced is just the vacuum uncertainty in the difference of the phase quadrature amplitudes of the light fields in the arms, and only at modulation frequencies at which signals are expected. This is achieved by injecting a (broadband) squeezed vacuum field (Fig. 1e) into the unused interferometer input port (Fig. 3). Ideally, perfect interference with the bright field is achieved. For this the squeezed field has to be in the same mode as the bright light, i.e. has to have the same wavelength, same polarisation, same wavefront curvature, same beam radius, and, of course, the same directions of propagation in the interferometer arms. For the squeezed-light enhancement of a Michelson interferometer operated at dark fringe, a polarising beam splitter in combination with a Faraday rotator is required. This combination constitutes an optical diode. Without any loss, the squeezed field is overlapped with the bright field at the interferometer's central beam splitter, is split and travels along the arms, is retro-reflected, constructively interferes and overlaps with the interferometer signal towards the photo diode. Due to the polarisation rotation of the Faraday rotator, the optical loss on signal and squeezed field is zero (in the ideal case). Generally, the purpose of an interferometer is to transform a differential phase modulation (of two light beams) into an amplitude modulation of the output light . Accordingly, the injected vacuum-squeezed field is injected such that the differential phase quadrature uncertainty in the arms is squeezed. On the output light amplitude quadrature squeezing is observed. Fig. 4 shows the photo voltage of the photo diode in the interferometer output port. Subtracting the constant offset provides the (GW) signal.

A source of squeezed states of light were integrated in the gravitational-wave detector GEO600 in 2010, as shown in Fig. 4. The source was built by the research group of R. Schnabel at Leibniz Universität Hannover (Germany). With squeezed light, the sensitivity of GEO600 during observational runs has been increased to values, which for practical reasons were not achievable without squeezed light. In 2018, squeezed light upgrades are also planned for the gravitational wave detectors Advanced LIGO and Advanced Virgo.

Going beyond squeezing of photon counting noise, squeezed states of light can also be used to correlate quantum measurement noise (shot noise) and quantum back action noise to achieve sensitivities in the quantum non-demolition (QND) regime.

Radiometry and calibration of quantum efficiencies

Squeezed light can be used in radiometry to calibrate the quantum efficiency of photo-electric photo detectors without a lamp of calibrated radiance. Here, the term photo detector refers to a device that measures the power of a bright beam, typically in the range from a few microwatts up to about 0.1 W. The typical example is a PIN photo diode. In case of perfect quantum efficiency (100%), such a detector is supposed to convert every photon energy of incident light into exactly one photo electron. Conventional techniques of measuring quantum efficiencies require the knowledge of how many photons hit the surface of the photo detector, i.e. they require a lamp of calibrated radiance. The calibration on the basis of squeezed states of light uses instead the effect, that the uncertainty product $\Delta^2 X_ \cdot \Delta^2 Y_$ increases the smaller the quantum uncertainty of the detector is. In other words: The squeezed light method uses the fact that squeezed states of light are sensitive against decoherence. Without any decoherence during generation, propagation and detection of squeezed light, the uncertainty product has its minimum value of 1/16 (see above). If optical loss is the dominating decoherence effect, which usually is the case, the independent measurement of all optical losses during generation and propagation together with the value of the uncertainty product directly reveals the quantum uncertainty of the photo detectors used.

When a squeezed state with squeezed variance $\Delta^2 X_$ is detected with a photo detector of quantum efficiency $\eta$ (with $0 \leq \eta \leq 1$), the actually observed variance is increased to
: $\Delta^2 X^\mathrm_ = \eta \cdot \Delta^2 X_ + (1-\eta)/4 \, .$
Optical loss mixes a portion of the vacuum state variance to the squeezed variance, which decreases the squeeze factor. The same equation also describes the influence of a non-perfect quantum efficiency on the anti-squeezed variance. The anti-squeezed variance reduces, however, the uncertainty product increases. Optical loss on a pure squeezed state produces a mixed squeezed state.

Entanglement-based quantum key distribution

Squeezed states of light can be used to produce Einstein-Podolsky-Rosen-entangled light that is the resource for a high quality level of quantum key distribution (QKD), which is called 'one-sided device independent QKD'.

Superimposing on a balanced beam splitter two identical light beams that carry squeezed modulation states and have a propagation length difference of a quarter of their wavelength produces two EPR entangled light beams at the beam splitter output ports. Quadrature amplitude measurements on the individual beams reveal uncertainties that are much larger than those of the ground states, but the data from the two beams show strong correlations: from a measurement value taken at the first beam ($X^A_$), one can infer the corresponding measurement value taken at the second beam ($X^B_$). If the inference shows an uncertainty smaller than that of the vacuum state, EPR correlations exist, see Fig. 5.

The aim of quantum key distribution is the distribution of identical, true random numbers to two distant parties A and B in such a way that A and B can quantify the amount of information about the numbers that has been lost to the environment (and thus is potentially in hand of an eavesdropper). To do so, sender (A) sends one of the entangled light beams to receiver (B). A and B measure repeatedly and simultaneously (taking the different propagation times into account) one of two orthogonal quadrature amplitudes. For every single measurement they need to choose whether to measure $X$ or $Y$ in a truly random way, independently from each other. By chance, they measure the same quadrature in 50% of the single measurements. After having performed a large number of measurements, A and B communicate (publicly) what their choice was for every measurement. The non-matched pairs are discarded. From the remaining data they make public a small but statistically significant amount to test whether B is able to precisely infer the measurement results at A. Knowing the characteristics of the entangled light source and the quality of the measurement at the sender site, the sender gets information about the decoherence that happened during channel transmission and during the measurement at B. The decoherence quantifies the amount of information that was lost to the environment. If the amount of lost information is not too high and the data string not too short, data post processing in terms of error correction and privacy amplification produces a key with an arbitrarily reduced epsilon-level of insecurity. In addition to conventional QKD, the test for EPR correlations not only characterizes the channel over which the light was sent (for instance a glas fibre) but also the measurement at the receiver site. The sender does not need to trust the receivers measurement any more. This higher quality of QKD is called ''one-sided device independent''. This type of QKD works if the natural decoherence is not too high. For this reason, an implementation that uses conventional telecommunication glas fibers would be limited to a distance of a few kilometers.

Generation

Squeezed light is produced by means of nonlinear optics. The most successful method uses degenerate type I optical- parametric down-conversion (also called optical-parametric amplification) inside an optical resonator. To squeeze modulation states with respect to a carrier field at optical frequency $\nu$, a bright pump field at twice the optical frequency is focussed into a nonlinear crystal that is placed between two or more mirrors forming an optical resonator. It is not necessary to inject light at frequency $\nu$. (Such light, however, is required for detecting the (squeezed) modulation states). The crystal material needs to have a nonlinear susceptibility and needs to be highly transparent for both optical frequencies used. Typical materials are lithium niobate (LiNbO₃) and (periodically poled) potassium titanyl phosphate (KTP). Due to the nonlinear susceptibility of the pumped crystal material, the electric field at frequency $\nu$ is amplified and deamplified, depending on the relative phase to the pump light. At the pump's electric field maxima, the electric field at frequency $\nu$ is amplified. At the pump's electric field minima, the electric field at frequency $\nu$ is squeezed. This way, the vacuum state (Fig. 1e) is transferred to a squeezed vacuum state (Fig. 1d). A displaced coherent state (Fig. 1a) is transferred to a phase squeezed state (Fig. 1b) or to an amplitude squeezed state (Fig. 1c), depending on the relative phase between coherent input field and pump field. A graphical description of these processes can be found in.

The existence of a resonator for the field at $\nu$ is essential. The task of the resonator is shown in Fig. 6. The left resonator mirror has a typical reflectivity of about $r^2_1=90\%$. Correspondingly $\sqrt$ of the electric field that (continuously) enters from the left gets reflected. The remaining part is transmitted and resonates between the two mirrors. Due to the resonance, the electric field inside the resonator gets enhanced (even without any medium inside). $10\%$ of the steady-state light power inside the resonator gets transmitted towards the left and interferes with the beam that was retro-reflected directly. For an empty loss-less resonator, 100% of the light power would eventually propagate towards the left, obeying energy conservation.

The principle of the ''squeezing'' ''resonator'' is the following: The medium parametrically attenuates the electric field inside the resonator to such a value that perfect ''destructive'' interference is achieved outside the resonator for the attenuated field quadrature. The optimum ''field'' attenuation factor inside the resonator is slightly below 2, depending on the reflectivity of the resonator mirror. This principle also works for electric field ''uncertainties''. Inside the resonator, the squeeze factor is always less than 6 dB, but outside the resonator it can be arbitrarily high. If quadrature $X_$ is squeezed, quadrature $Y_$ is anti-squeezed – inside as well as outside the resonator. It can be shown that the highest squeeze factor for ''one'' quadrature is achieved if the resonator is at its threshold for the ''orthogonal'' quadrature. At threshold and above, the pump field is converted into a bright field at optical frequency $\nu$. Squeezing resonators are usually operated slightly ''below'' threshold, for instance, to avoid damage to the photo diodes due to the bright down-converted field.

A squeezing resonator works efficiently at modulation frequencies well inside its linewidth. Only for these frequencies highest squeeze factors can be achieved. At frequencies the optical-parametric gain is strongest, and the time delay between the interfering parts negligible. If decoherence was zero, ''infinite'' squeeze factors could be achieved outside the resonator, although the squeeze factor ''inside'' the resonator was less than 6 dB. Squeezing resonators have typical linewidths of a few tens of MHz up to GHz.

Due to the interest in the interaction between squeezed light and atomic ensemble, narrowband atomic resonance squeezed light have been also generated through crystal and the atomic medium.

Detection

Squeezed states of light can be fully characterized by a photo-electric detector that is able to (subsequently) measure the electric field strengths at any phase $\vartheta$. (The restriction to a certain band of modulation frequencies happens after the detection by electronic filtering.) The required detector is a balanced homodyne detector (BHD). It has two input ports for two light beams. One for the (squeezed) signal field, and another for the BHDs local oscillator (LO) having the same wavelength as the signal field. The LO is part of the BHD. Its purpose is to beat with the signal field and to optically amplify it. Further components of the BHD are a balanced beam splitter and two photo diodes (of high quantum efficiency). Signal beam and LO need to be overlapped at the beam splitter. The two interference results in the beam splitter output ports are detected and the difference signal recorded (Fig. 7). The LO needs to be much more intense than the signal field. In this case the differential signal from the photo diodes in the interval $f \pm \Delta f/2$ is proportional to the quadrature amplitude $X_$. Changing the differential propagation length before the beam splitter sets the quadrature angle to an arbitrary value. (A change by a quarter of the optical wavelength changes the phase by  $\pi/2$.)

The following should be stated at this point: Any information about the electro-magnetic wave can only be gathered in a quantized way, i.e. by absorbing light quanta (photons). This is also true for the BHD. However, a BHD cannot resolve the discrete energy transfer from the light to the electric current, since in any small time interval a vast number of photons are detected. This is ensured by the intense LO. The observable therefore has a quasi-continuous eigenvalue spectrum, as it is expected for an electric field strength. (In principle, one can also characterize squeezed states, in particular squeezed ''vacuum'' states, by counting photons, however, in general the measurement of the photon number statistic is not sufficient for a full characterization of a squeezed state and the full density matrix in the basis of the number states has to be determined.)

See also

* Spin squeezed state

References

{{reflist

Quantum states
Light