In music theory, the spiral array model is an extended type of

pitch space In music theory, pitch spaces model relationships between pitches. These models typically use distance to model the degree of relatedness, with closely related pitches placed near one another, and less closely related pitches placed farther ap ...

. A mathematical model involving concentric

helices A helix () is a shape like a corkscrew or spiral staircase. It is a type of smooth space curve with tangent lines at a constant angle to a fixed axis. Helices are important in biology, as the DNA molecule is formed as two intertwined helice ...

(an "array of

spiral In mathematics, a spiral is a curve which emanates from a point, moving farther away as it revolves around the point. Helices Two major definitions of "spiral" in the American Heritage Dictionary are:pitches,

chords Chord may refer to: * Chord (music), an aggregate of musical pitches sounded simultaneously ** Guitar chord a chord played on a guitar, which has a particular tuning * Chord (geometry), a line segment joining two points on a curve * Chord ...

, and

keys Key or The Key may refer to: Common meanings * Key (cryptography), a piece of information that controls the operation of a cryptography algorithm * Key (lock), device used to control access to places or facilities restricted by a lock * Key (ma ...

in the same geometric space. It was proposed in 2000 by Elaine Chew in her MIT doctoral thesis ''Toward a Mathematical Model of

Tonality Tonality is the arrangement of pitches and/or chords of a musical work in a hierarchy of perceived relations, stabilities, attractions and directionality. In this hierarchy, the single pitch or triadic chord with the greatest stability is cal ...

''. Further research by Chew and others have produced modifications of the spiral array model, and, applied it to various problems in music theory and practice, such as key finding (symbolic and audio), pitch spelling, tonal segmentation, similarity assessment, and musical humor. The extensions and applications are described in ''Mathematical and Computational Modeling of Tonality: Theory and Applications''. The spiral array model can be viewed as a generalized

tonnetz In musical tuning and harmony, the (German for 'tone network') is a conceptual lattice diagram representing tonal space first described by Leonhard Euler in 1739. Various visual representations of the ''Tonnetz'' can be used to show tradit ...

, which maps pitches into a two-dimensional lattice (array) structure. The spiral array wraps up the two-dimensional

into a three-dimensional lattice, and models higher order structures such as chords and keys in the interior of the lattice space. This allows the spiral array model to produce geometric interpretations of relationships between low- and high-level structures. For example, it is possible to model and measure geometrically the distance between a particular pitch and a particular key, both represented as points in the spiral array space. To preserve pitch spelling, because musically A# ≠ Bb in their function and usage, the spiral array does not assume

enharmonic equivalence In modern musical notation and tuning, an enharmonic equivalent is a note, interval, or key signature that is equivalent to some other note, interval, or key signature but "spelled", or named differently. The enharmonic spelling of a written ...

, i.e. it does not fold into a torus. The spatial relationships between pitches, between chords, and between keys agree with those in other representations of tonal space. The model and its real-time algorithms have been implemented in the tonal visualization software MuSA.RT (Music on the Spiral Array . Real-Time) and a free app, MuSA_RT, both of which have been used in music education videos and in live performance.

Structure of the spiral array

The model as proposed covers basic pitches, major chords, minor chords, major keys and minor keys, represented on five concentric helices. Starting with a formulation of the pitch helix, inner helices are generated as

convex combination In convex geometry and vector algebra, a convex combination is a linear combination of points (which can be vectors, scalars, or more generally points in an affine space) where all coefficients are non-negative and sum to 1. In other ...

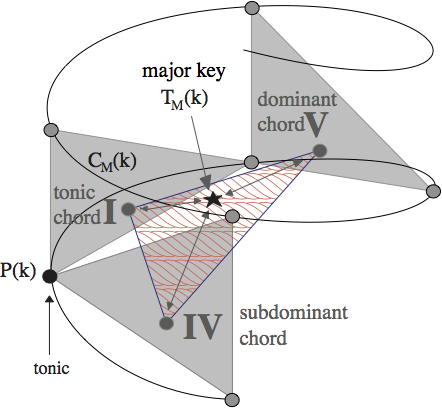
s of points on outer ones. For example, the pitches C, E, and G are represented as the Cartesian points ''P''(0), ''P''(1), and ''P''(4) (see definitions in next section), which outline a triangle. The convex combination of these three points is a point inside the triangle, and represents their ''center of effect'' (''ce''). This interior point, ''C''_''M''(0), represents the C major chord in the spiral array model. Similarly, keys may be constructed by the centers of effect of their I, IV, and V chords. * The outer helix represents pitches classes. Neighboring pitch classes are a music interval of a

perfect fifth In music theory, a perfect fifth is the musical interval corresponding to a pair of pitches with a frequency ratio of 3:2, or very nearly so. In classical music from Western culture, a fifth is the interval from the first to the last of five ...

, and spatially a quarter rotation, apart. The order of the pitch classes can be determined by the line of fifths. For example, C would be followed by G (C and G are a perfect fifth apart), which would be followed D (G and D are a perfect fifth apart), etc. As a result of this structure, and one of the important properties leading to its selection, vertical neighbors are a music interval of a

major third In classical music, a third is a musical interval encompassing three staff positions (see Interval number for more details), and the major third () is a third spanning four semitones. Forte, Allen (1979). ''Tonal Harmony in Concept and P ...

apart. Thus, a pitch class's nearest neighbors and itself form perfect fifth and major third intervals. * By taking every consecutive triads along the helix, and connecting their centers of effect, a second helix is formed inside the pitch helix, representing the major chords. * Similarly, by taking the proper minor triads and connecting their centers of effect, a third helix is formed, representing the minor chords. * The major key helix is formed by the centers of effect of the centers of effect of the I, IV, and V chords *The minor key helix is formed by connecting similar combinations of the i, iv/IV, and V/v chords.

Equations for pitch, chord, and key representations

Spiral Array Model–Major Key Representation

Spiral Array Model—Minor Key Representation

In Chew's model, the pitch class helix, P, is represented in parametric form by:

P(k) = \begin
x_ \\
y_ \\
z_ \\
\end = \begin
r \sin (k \cdot \pi / 2)\\
r \cos (k \cdot \pi / 2) \\
kh
\end

where ''k'' is an integer representing the pitch's distance from C along the line of fifths, ''r'' is the radius of the spiral, and ''h'' is the "rise" of the spiral. The major chord helix, C_M is represented by: :

C_M(k) = w_1 \cdot P(k) + w_2 \cdot P(k + 1) + w_3 \cdot P(k+4)

where

w_ \ge w_ \ge w_ > 0

and

\sum_^3 w_ = 1

. The weights "w" affect how close the center of effect are to the fundamental, major third, and perfect fifth of the chord. By changing the relative values of these weights, the spiral array model controls how "close" the resulting chord is to the three constituent pitches. Generally in western music, the fundamental is given the greatest weight in identifying the chord (w1), followed by the fifth (w2), followed by the third (w3). The minor chord helix, C_m is represented by: :

C_m(k) = u_1 \cdot P(k) + u_2 \cdot P(k + 1) + u_3 \cdot P(k-3)

where

u_1 \ge u_2 \ge u_3 > 0

and

\sum_^3 u_i = 1.

The weights "u" function similarly to the major chord. The major key helix, T_M is represented by: :

T_M(k) = \omega_1 \cdot P(k) + \omega_2 \cdot P(k + 1) + \omega_3 \cdot P(k-1)

where

\omega_1 \ge \omega_2 \ge \omega_3 > 0

and

\sum_^3 \omega_i = 1

. Similar to the weights controlling how close constituent pitches are to the center of effect of the chord they produce, the weights

\omega

control the relative effect of the I, IV, and V chord in determining how close they are to the resultant key. The minor key helix, T_m is represented by: :

T_m(k) = \nu_1 \cdot C_M(k) + \nu_2 \cdot (\alpha \cdot C_M(k+1) + (1-\alpha) \cdot C_m(k+1)) + \nu_3 \cdot (\beta * C_m(k-1) + (1 - \beta) \cdot C_M(k-1)).

where

\nu_1 \ge \nu_2 \ge \nu_3 > 0

and

\nu_1 + \nu_2 + \nu_3 = 1

and

0 \ge \alpha \ge 1

and

\beta \ge 1

Structure of the spiral array

Equations for pitch, chord, and key representations

References

Further reading