sphericon

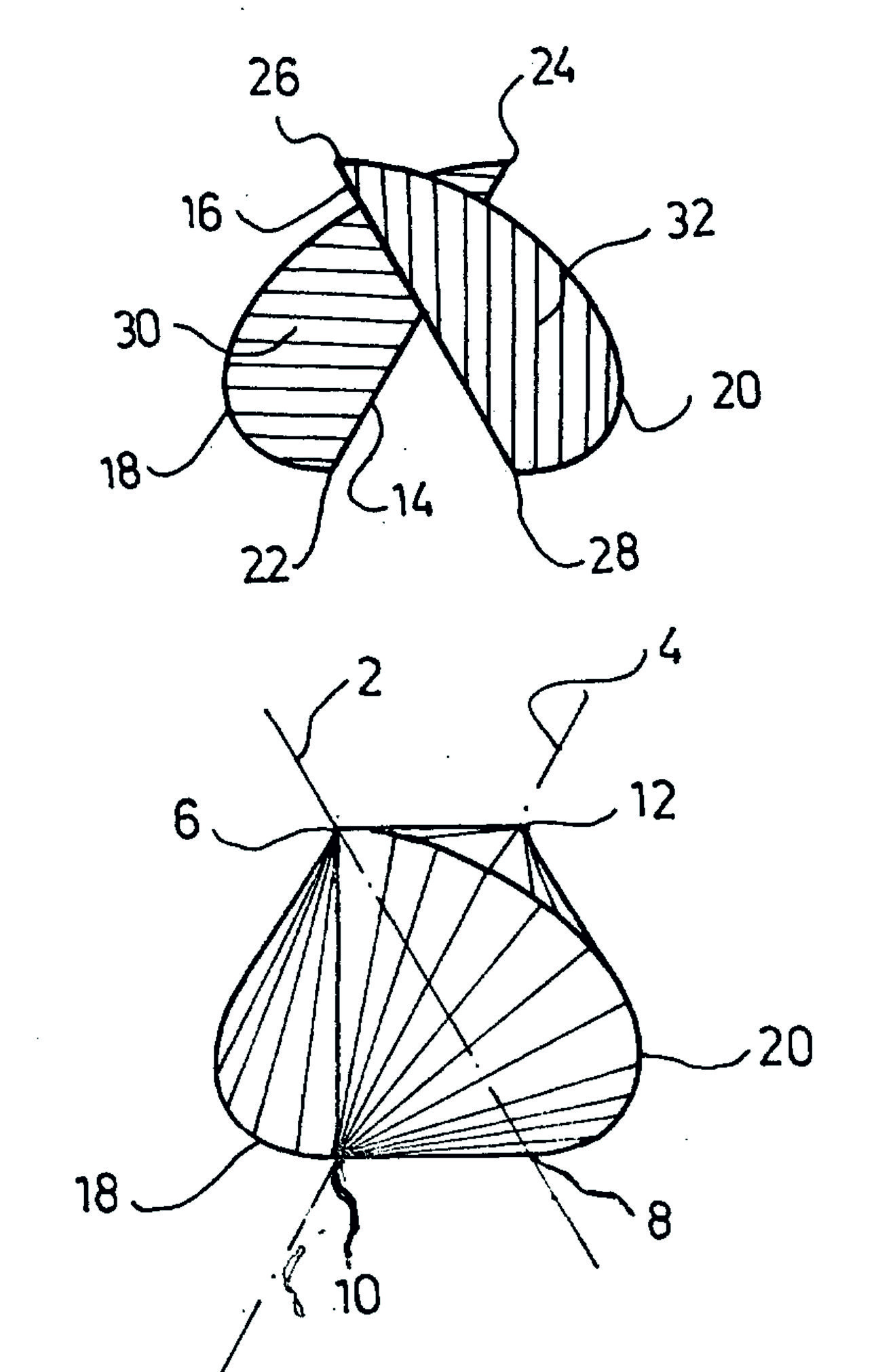
In solid geometry, the sphericon is a solid that has a continuous developable surface with two congruent, semi-circular edges, and four vertices that define a square. It is a member of a special family of rollers that, while being rolled on a flat surface, bring all the points of their surface to contact with the surface they are rolling on. It was discovered independently by carpenter Colin Roberts (who named it) in the UK in 1969, by dancer and sculptor Alan Boeding of MOMIX in 1979, and by inventor David Hirsch, who patented it in Israel in 1980.

Construction

The sphericon may be constructed from a bicone (a double cone) with an apex angle of 90 degrees, by splitting the bicone along a plane through both apexes, rotating one of the two halves by 90 degrees, and reattaching the two halves.
Alternatively, the surface of a sphericon can be formed by cutting and gluing a paper template in the form of four circular sectors (with central angles $\pi/\sqrt$) joined edge-to-edge.

Geometric properties

The surface area of a sphericon with radius $r$ is given by
:$S = 2\sqrt\pi r^2$.
The volume is given by
:$V = \frac\pi r^3$,
exactly half the volume of a sphere with the same radius.

History

Around 1969, Colin Roberts (a carpenter from the UK) made a sphericon out of wood while attempting to carve a Möbius strip without a hole.

In 1979, David Hirsch invented a device for generating a meander motion. The device consisted of two perpendicular half discs joined at their axes of symmetry. While examining various configurations of this device, he discovered that the form created by joining the two half discs, exactly at their diameter centers, is actually a skeletal structure of a solid made of two half bicones, joined at their square cross-sections with an offset angle of 90 degrees, and that the two objects have exactly the same meander motion. Hirsch filed a patent in Israel in 1980, and a year later, a pull toy named Wiggler Duck, based on Hirsch's device, was introduced by Playskool Company.

In 1999, Colin Roberts sent Ian Stewart a package containing a letter and two sphericon models. In response, Stewart wrote an article "Cone with a Twist" in his Mathematical Recreations column of ''Scientific American''. This sparked quite a bit of interest in the shape, and has been used by Tony Phillips to develop theories about mazes. Roberts' name for the shape, the sphericon, was taken by Hirsch as the name for his company, Sphericon Ltd.

In popular culture

In 1979, modern dancer Alan Boeding designed his "Circle Walker" sculpture from two crosswise semicircles, a skeletal version of the sphericon. He began dancing with a scaled-up version of the sculpture in 1980 as part of an MFA program in sculpture at Indiana University, and after he joined the MOMIX dance company in 1984 the piece became incorporated into the company's performances. The company's later piece "Dream Catcher" is based around a similar Boeding sculpture whose linked teardrop shapes incorporate the skeleton and rolling motion of the oloid, a similar rolling shape formed from two perpendicular circles each passing through the center of the other.

In 2008, British woodturner David Springett published the book "Woodturning Full Circle", which explains how sphericons (and other unusual solid forms, such as streptohedrons) can be made on a wood lathe.

References

External links

{{wiktionary, sphericon
Sphericon construction animation at the National Curve Bank website.

Paper model of a sphericon
Make a sphericon

using regular polygons with different numbers of sides
A Sphericon in Motion
showing the characteristic wobbly motion as it rolls across a flat surface

Geometric shapes