Spectrum (homotopy Theory) on:
[Wikipedia]
[Google]
[Amazon]
A spectrum (: spectra or spectrums) is a set of related ideas, objects, or properties whose features overlap such that they blend to form a continuum. The word ''spectrum'' was first used scientifically in
 In
In
optics
Optics is the branch of physics that studies the behaviour and properties of light, including its interactions with matter and the construction of optical instruments, instruments that use or Photodetector, detect it. Optics usually describes t ...
to describe the rainbow of colors in visible light after passing through a prism. In the optical spectrum, light wavelength
In physics and mathematics, wavelength or spatial period of a wave or periodic function is the distance over which the wave's shape repeats.
In other words, it is the distance between consecutive corresponding points of the same ''phase (waves ...
is viewed as continuous, and spectral colors are seen to blend into one another smoothly when organized in order of their corresponding wavelengths. As scientific understanding of light advanced, the term came to apply to the entire electromagnetic spectrum
The electromagnetic spectrum is the full range of electromagnetic radiation, organized by frequency or wavelength. The spectrum is divided into separate bands, with different names for the electromagnetic waves within each band. From low to high ...
, including radiation not visible to the human eye.
''Spectrum'' has since been applied by analogy to topics outside optics. Thus, one might talk about the " spectrum of political opinion", or the "spectrum of activity" of a drug, or the "autism spectrum
Autism, also known as autism spectrum disorder (ASD), is a neurodevelopmental disorder characterized by differences or difficulties in social communication and interaction, a preference for predictability and routine, sensory processing d ...
". In these uses, values within a spectrum may not be associated with precisely quantifiable numbers or definitions. Such uses imply a broad range of conditions or behaviors grouped together and studied under a single title for ease of discussion. Nonscientific uses of the term ''spectrum'' are sometimes misleading. For instance, a single left–right spectrum of political opinion does not capture the full range of people's political beliefs. Political scientists use a variety of biaxial and multiaxial systems to more accurately characterize political opinion.
In most modern usages of ''spectrum'' there is a unifying theme between the extremes at either end. This was not always true in older usage.
Etymology
InLatin
Latin ( or ) is a classical language belonging to the Italic languages, Italic branch of the Indo-European languages. Latin was originally spoken by the Latins (Italic tribe), Latins in Latium (now known as Lazio), the lower Tiber area aroun ...
, ''spectrum'' means "image" or " apparition", including the meaning " spectre". Spectral evidence is testimony about what was done by spectres of persons not present physically, or hearsay
Hearsay, in a legal forum, is an out-of-court statement which is being offered in court for the truth of what was asserted. In most courts, hearsay evidence is Inadmissible evidence, inadmissible (the "hearsay evidence rule") unless an exception ...
evidence about what ghosts or apparitions of Satan said. It was used to convict a number of persons of witchcraft
Witchcraft is the use of Magic (supernatural), magic by a person called a witch. Traditionally, "witchcraft" means the use of magic to inflict supernatural harm or misfortune on others, and this remains the most common and widespread meanin ...
at Salem, Massachusetts
Salem ( ) is a historic coastal city in Essex County, Massachusetts, United States, located on the North Shore (Massachusetts), North Shore of Greater Boston. Continuous settlement by Europeans began in 1626 with English colonists. Salem was one ...
in the late 17th century. The word "spectrum" pektrumwas strictly used to designate a ghostly optical afterimage
An afterimage, or after-image, is an image that continues to appear in the eyes after a period of exposure to the original image. An afterimage may be a normal phenomenon (physiological afterimage) or may be pathological (palinopsia). Illusory ...
by Goethe
Johann Wolfgang (von) Goethe (28 August 1749 – 22 March 1832) was a German polymath who is widely regarded as the most influential writer in the German language. His work has had a wide-ranging influence on Western literature, literary, Polit ...
in his '' Theory of Colors'' and Schopenhauer in '' On Vision and Colors''.
The prefix "spectro-" is used to form words relating to spectra. For example, a spectrometer is a device used to record spectra and spectroscopy
Spectroscopy is the field of study that measures and interprets electromagnetic spectra. In narrower contexts, spectroscopy is the precise study of color as generalized from visible light to all bands of the electromagnetic spectrum.
Spectro ...
is the use of a spectrometer for chemical analysis
Analytical chemistry studies and uses instruments and methods to separate, identify, and quantify matter. In practice, separation, identification or quantification may constitute the entire analysis or be combined with another method. Separa ...
.
Physical sciences
Biological science
Antibiotic
An antibiotic is a type of antimicrobial substance active against bacteria. It is the most important type of antibacterial agent for fighting pathogenic bacteria, bacterial infections, and antibiotic medications are widely used in the therapy ...
spectrum of activity is a component of antibiotic classification. A broad-spectrum antibiotic is active against a wide range of bacteria, whereas a narrow-spectrum antibiotic is effective against specific families of bacteria.S.J. Hopkins, Drugs and Pharmacology for Nurses 12th ed., 1997 () An example of a commonly used broad-spectrum antibiotic is ampicillin
Ampicillin is an antibiotic belonging to the aminopenicillin class of the penicillin family. The drug is used to prevent and treat several bacterial infections, such as respiratory tract infections, urinary tract infections, meningitis, s ...
. An example of a narrow spectrum antibiotic is Dicloxacillin, which acts on beta-lactamase-producing Gram-positive
In bacteriology, gram-positive bacteria are bacteria that give a positive result in the Gram stain test, which is traditionally used to quickly classify bacteria into two broad categories according to their type of cell wall.
The Gram stain is ...
bacteria such as ''Staphylococcus aureus
''Staphylococcus aureus'' is a Gram-positive spherically shaped bacterium, a member of the Bacillota, and is a usual member of the microbiota of the body, frequently found in the upper respiratory tract and on the skin. It is often posi ...
''.
In psychiatry, the spectrum approach uses the term spectrum to describe a range of linked conditions, sometimes also extending to include singular symptoms and traits. For example, the autism spectrum
Autism, also known as autism spectrum disorder (ASD), is a neurodevelopmental disorder characterized by differences or difficulties in social communication and interaction, a preference for predictability and routine, sensory processing d ...
describes a range of conditions classified as neurodevelopmental disorders.
Mathematics
Inmathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many ar ...
, the spectrum of a matrix is the multiset of the eigenvalues of the matrix.
In functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure (for example, Inner product space#Definition, inner product, Norm (mathematics ...
, the concept of the spectrum of a bounded operator is a generalization of the eigenvalue concept for matrices.
In algebraic topology
Algebraic topology is a branch of mathematics that uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariant (mathematics), invariants that classification theorem, classify topological spaces up t ...
, a spectrum
A spectrum (: spectra or spectrums) is a set of related ideas, objects, or properties whose features overlap such that they blend to form a continuum. The word ''spectrum'' was first used scientifically in optics to describe the rainbow of co ...
is an object representing a generalized cohomology theory.
Social science
 In
In social science
Social science (often rendered in the plural as the social sciences) is one of the branches of science, devoted to the study of societies and the relationships among members within those societies. The term was formerly used to refer to the ...
, economic spectrum is used to indicate the range of social class along some indicator of wealth or income. In political science
Political science is the scientific study of politics. It is a social science dealing with systems of governance and Power (social and political), power, and the analysis of political activities, political philosophy, political thought, polit ...
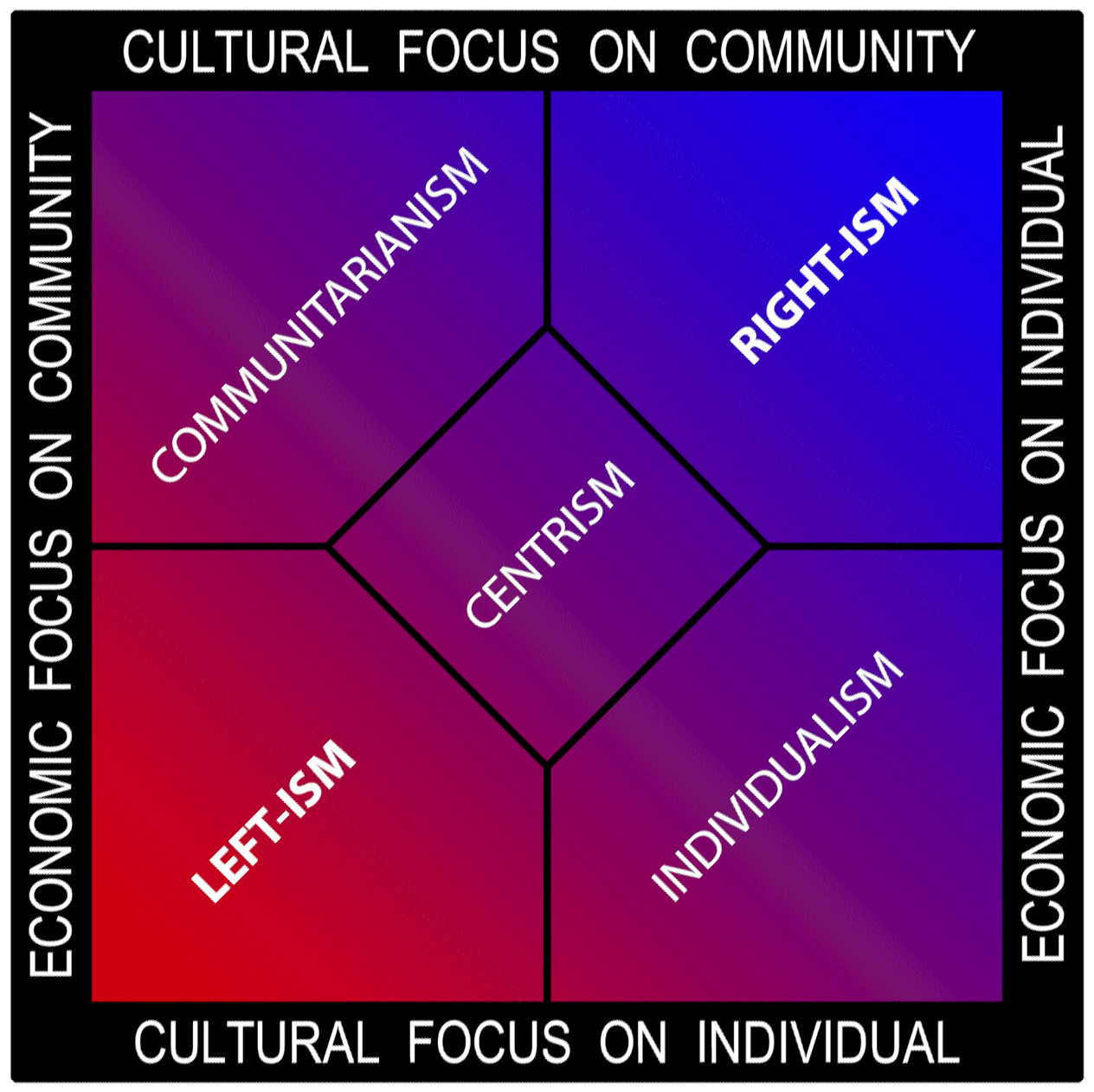
, the term political spectrum
A political spectrum is a system to characterize and classify different Politics, political positions in relation to one another. These positions sit upon one or more Geometry, geometric Coordinate axis, axes that represent independent political ...
refers to a system of classifying political positions in one or more dimensions, for example in a range including right wing and left wing.
References
{{Authority control Concepts in physics Light Broad-concept articles