Solvency Cone on:
[Wikipedia]
[Google]
[Amazon]
The solvency cone is a concept used in
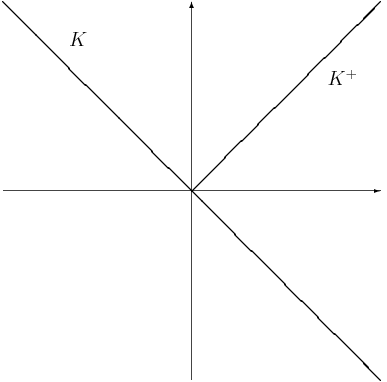
 Assume there are 2 assets, A and M with 1 to 1 exchange possible.
Assume there are 2 assets, A and M with 1 to 1 exchange possible.
financial mathematics
Mathematical finance, also known as quantitative finance and financial mathematics, is a field of applied mathematics, concerned with mathematical modeling of financial markets.
In general, there exist two separate branches of finance that require ...
which models the possible trades in the financial market
A financial market is a market in which people trade financial securities and derivatives at low transaction costs. Some of the securities include stocks and bonds, raw materials and precious metals, which are known in the financial mark ...
. This is of particular interest to markets with transaction costs
In economics and related disciplines, a transaction cost is a cost in making any economic trade when participating in a market. Oliver E. Williamson defines transaction costs as the costs of running an economic system of companies, and unlike pro ...
. Specifically, it is the convex cone
In linear algebra, a ''cone''—sometimes called a linear cone for distinguishing it from other sorts of cones—is a subset of a vector space that is closed under scalar multiplication; that is, is a cone if x\in C implies sx\in C for every .
...
of portfolios that can be exchanged to portfolios of non-negative components (including paying of any transaction costs).
Mathematical basis
If given a bid-ask matrix for assets such that and is the number of assets which with any non-negative quantity of them can be "discarded" (traditionally ), then the solvency cone is the convex cone spanned by the unit vectors and the vectors .Definition
A solvency cone is any closed convex cone such that and .Uses
A process of (random) solvency cones is a model of a financial market. This is sometimes called a market process. The negative of a solvency cone is the set of portfolios that can be obtained starting from the zero portfolio. This is intimately related to self-financing portfolios. The dual cone of the solvency cone () are the set of prices which would define a friction-less pricing system for the assets that is consistent with the market. This is also called a consistent pricing system.Examples

 Assume there are 2 assets, A and M with 1 to 1 exchange possible.
Assume there are 2 assets, A and M with 1 to 1 exchange possible.
Frictionless market
In africtionless market
Frictionless can refer to:
* Frictionless market
* Frictionless continuant
* Frictionless sharing
* Frictionless plane
* Frictionless flow
{{disambiguation ...
, we can obviously make (1A,-1M) and (-1A,1M) into non-negative portfolios, therefore . Note that (1,1) is the "price vector."
With transaction costs
Assume further that there is 50% transaction costs for each deal. This means that (1A,-1M) and (-1A,1M) cannot be exchanged into non-negative portfolios. But, (2A,-1M) and (-1A,2M) can be traded into non-negative portfolios. It can be seen that . The dual cone of prices is thus easiest to see in terms of prices of A in terms of M (and similarly done for price of M in terms of A): * someone offers 1A for tM: therefore there is arbitrage if * someone offers tM for 1A: therefore there is arbitrage ifProperties
If a solvency cone : * contains a line, then there is an exchange possible without transaction costs. * , then there is no possible exchange, i.e. the market is completely illiquid.References
{{Reflist Financial risk modeling