solar elevation angle on:
[Wikipedia]
[Google]
[Amazon]
The solar zenith angle is the zenith angle of the
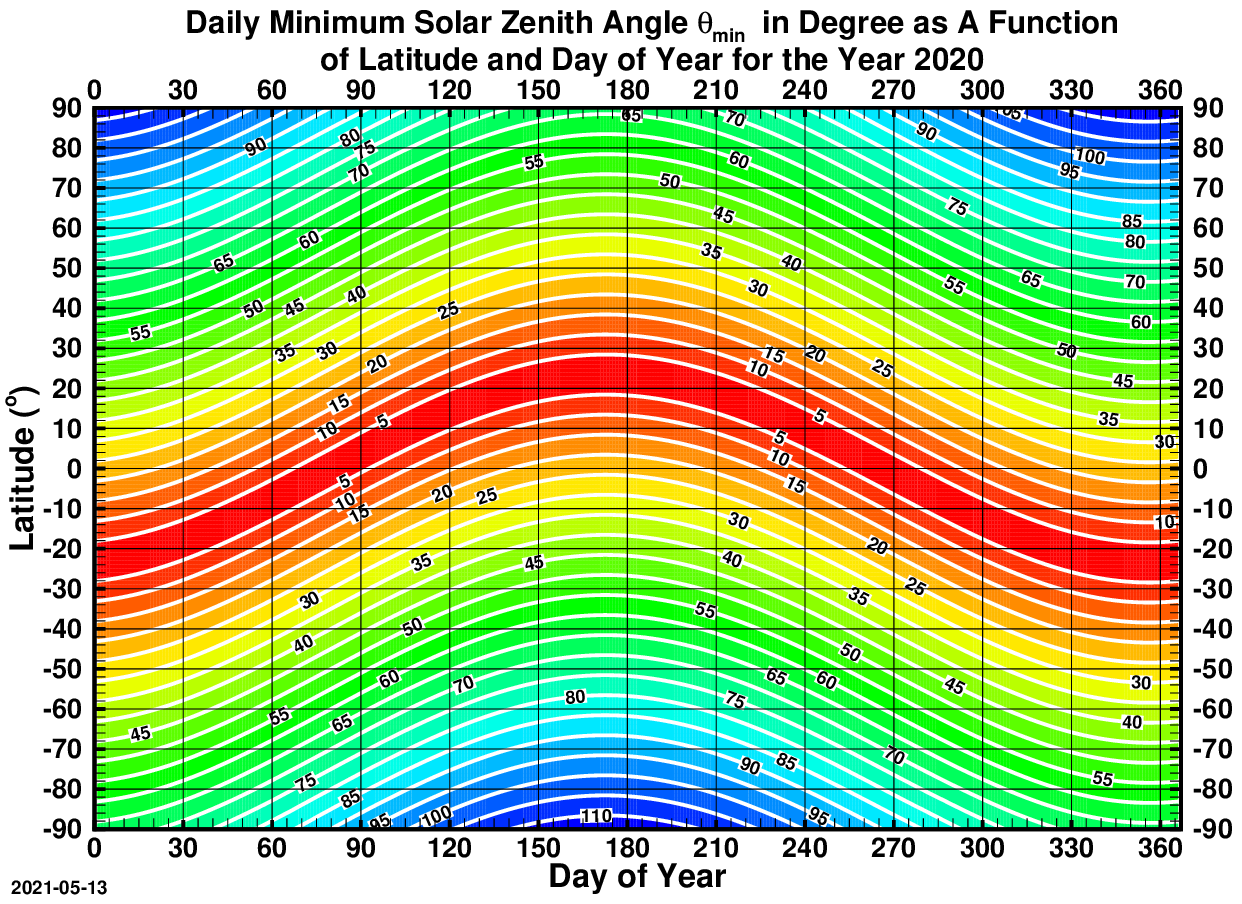
 At any given location on any given day, the solar zenith angle, , reaches its minimum, , at local solar noon when the hour angle , or , namely, , or . If , it is polar night.
And at any given location on any given day, the solar zenith angle, , reaches its maximum, , at local midnight when the hour angle , or , namely, , or . If , it is polar day.
At any given location on any given day, the solar zenith angle, , reaches its minimum, , at local solar noon when the hour angle , or , namely, , or . If , it is polar night.
And at any given location on any given day, the solar zenith angle, , reaches its maximum, , at local midnight when the hour angle , or , namely, , or . If , it is polar day.
sun
The Sun is the star at the centre of the Solar System. It is a massive, nearly perfect sphere of hot plasma, heated to incandescence by nuclear fusion reactions in its core, radiating the energy from its surface mainly as visible light a ...
, i.e., the angle between the sun’s rays and the vertical direction
In astronomy, geography, and related sciences and contexts, a ''Direction (geometry, geography), direction'' or ''plane (geometry), plane'' passing by a given point is said to be vertical if it contains the local gravity direction at that point. ...
. It is the complement to the solar altitude or solar elevation, which is the altitude angle
The horizontal coordinate system is a celestial coordinate system that uses the observer's local horizon as the fundamental plane to define two angles of a spherical coordinate system: altitude and ''azimuth''.
Therefore, the horizontal coordin ...
or elevation angle
The horizontal coordinate system is a celestial coordinate system that uses the observer's local horizon as the fundamental plane to define two angles of a spherical coordinate system: altitude and ''azimuth''.
Therefore, the horizontal coordin ...
between the sun’s rays and a horizontal plane
Horizontal may refer to:
*Horizontal plane, in astronomy, geography, geometry and other sciences and contexts
*Horizontal coordinate system, in astronomy
*Horizontalism, in monetary circuit theory
*Horizontalidad, Horizontalism, in sociology
*Hor ...
. At solar noon
Noon (also known as noontime or midday) is 12 o'clock in the daytime. It is written as 12 noon, 12:00 m. (for '' meridiem'', literally 12:00 midday), 12 p.m. (for ''post meridiem'', literally "after midday"), 12 pm, or 12:00 (using a 24-hour clo ...
, the altitude angle (complement of the solar angle) is at a minimum and is equal to latitude minus solar declination angle. This is the basis by which ancient mariners navigated the oceans. Solar zenith angle is normally used in combination with the solar azimuth angle to determine the position of the Sun
The position of the Sun in the sky is a function of both the time and the geographic coordinate system, geographic location of observation on Earth's surface. As Earth's orbit, Earth orbits the Sun over the course of a year, the Sun appears to mo ...
as observed from a given location on the surface of the Earth.
Formula
where * is the ''solar zenith angle'' * is the ''solar altitude angle'', * is thehour angle
In astronomy and celestial navigation, the hour angle is the dihedral angle between the '' meridian plane'' (containing Earth's axis and the zenith) and the '' hour circle'' (containing Earth's axis and a given point of interest).
It may be ...
, in the local solar time
Solar time is a calculation of the passage of time based on the position of the Sun in the sky. The fundamental unit of solar time is the day, based on the synodic rotation period. Traditionally, there are three types of time reckoning based ...
.
* is the current declination of the Sun
* is the local latitude
In geography, latitude is a geographic coordinate system, geographic coordinate that specifies the north-south position of a point on the surface of the Earth or another celestial body. Latitude is given as an angle that ranges from −90° at t ...
.
Derivation of the formula using the subsolar point and vector analysis
While the formula can be derived by applying the cosine law to the zenith-pole-Sun spherical triangle, thespherical trigonometry
Spherical trigonometry is the branch of spherical geometry that deals with the metrical relationships between the edge (geometry), sides and angles of spherical triangles, traditionally expressed using trigonometric functions. On the sphere, ge ...
is a relatively esoteric subject.
By introducing the coordinates of the subsolar point and using vector analysis, the formula can be obtained straightforward without incurring the use of spherical trigonometry.Zhang, T., Stackhouse, P.W., Macpherson, B., and Mikovitz, J.C., 2021. A solar azimuth formula that renders circumstantial treatment unnecessary without compromising mathematical rigor: Mathematical setup, application and extension of a formula based on the subsolar point and atan2 function. Renewable Energy, 172, 1333-1340. DOI: https://doi.org/10.1016/j.renene.2021.03.047
In the Earth-Centered Earth-Fixed ( ECEF) geocentric Cartesian coordinate system, let and be the latitudes and longitudes, or coordinates, of the subsolar point and the observer's point, then the upward-pointing unit vectors at the two points, and , are
where , and are the basis vectors in the ECEF coordinate system.
Now the cosine of the solar zenith angle, , is simply the dot product
In mathematics, the dot product or scalar productThe term ''scalar product'' means literally "product with a Scalar (mathematics), scalar as a result". It is also used for other symmetric bilinear forms, for example in a pseudo-Euclidean space. N ...
of the above two vectors
Note that is the same as , the declination of the Sun, and is equivalent to , where is the hour angle defined earlier. So the above format is mathematically identical to the one given earlier.
Additionally, Ref. also derived the formula for solar azimuth angle in a similar fashion without using spherical trigonometry.
Minimum and Maximum

 At any given location on any given day, the solar zenith angle, , reaches its minimum, , at local solar noon when the hour angle , or , namely, , or . If , it is polar night.
And at any given location on any given day, the solar zenith angle, , reaches its maximum, , at local midnight when the hour angle , or , namely, , or . If , it is polar day.
At any given location on any given day, the solar zenith angle, , reaches its minimum, , at local solar noon when the hour angle , or , namely, , or . If , it is polar night.
And at any given location on any given day, the solar zenith angle, , reaches its maximum, , at local midnight when the hour angle , or , namely, , or . If , it is polar day.
Caveats
The calculated values are approximations due to the distinction between common/geodetic latitude and geocentric latitude. However, the two values differ by less than 12 minutes of arc, which is less than the apparent angular radius of the sun. The formula also neglects the effect ofatmospheric refraction
Atmospheric refraction is the deviation of light or other electromagnetic wave from a straight line as it passes through the atmosphere due to the variation in air density as a function of height. This refraction is due to the velocity of light ...
.
Applications
Sunrise/Sunset
Sunset and sunrise occur (approximately) when the zenith angle is 90°, where the hour angle ''h''0 satisfies Precise times of sunset andsunrise
Sunrise (or sunup) is the moment when the upper rim of the Sun appears on the horizon in the morning, at the start of the Sun path. The term can also refer to the entire process of the solar disk crossing the horizon.
Terminology
Although the S ...
occur when the upper limb of the Sun appears, as refracted by the atmosphere, to be on the horizon.
Albedo
A weighted daily average zenith angle, used in computing the local albedo of the Earth, is given by where ''Q'' is the instantaneous irradiance.Summary of special angles
For example, the solar elevation angle is: * 90° at the subsolar point, which occurs, for example, at the equator on a day of equinox at solar noon * near 0° at the sunset or at the sunrise * between −90° and 0° during the night (midnight) An exact calculation is given inposition of the Sun
The position of the Sun in the sky is a function of both the time and the geographic coordinate system, geographic location of observation on Earth's surface. As Earth's orbit, Earth orbits the Sun over the course of a year, the Sun appears to mo ...
. Other approximations exist elsewhere.
See also
*Azimuth
An azimuth (; from ) is the horizontal angle from a cardinal direction, most commonly north, in a local or observer-centric spherical coordinate system.
Mathematically, the relative position vector from an observer ( origin) to a point ...
* Solar azimuth angle
* Horizontal coordinate system
The horizontal coordinate system is a celestial coordinate system that uses the observer's local horizon as the fundamental plane to define two angles of a spherical coordinate system: altitude and ''azimuth''.
Therefore, the horizontal coord ...
* List of orbits
This is a list of types of gravitational orbit classified by various characteristics.
Common abbreviations
List of abbreviations of common Earth orbits
List of abbreviations of other orbits
Classifications
The following is a list of t ...
*
* Position of the Sun
The position of the Sun in the sky is a function of both the time and the geographic coordinate system, geographic location of observation on Earth's surface. As Earth's orbit, Earth orbits the Sun over the course of a year, the Sun appears to mo ...
* Sun path
Sun path, sometimes also called day arc, refers to the diurnal motion, daily (sunrise to sunset) and seasonal arc (geometry), arc-like path that the Sun appears to follow across the sky as the Earth Earth's rotation, rotates and Earth's orbi ...
* Sunrise
Sunrise (or sunup) is the moment when the upper rim of the Sun appears on the horizon in the morning, at the start of the Sun path. The term can also refer to the entire process of the solar disk crossing the horizon.
Terminology
Although the S ...
* Sunset
Sunset (or sundown) is the disappearance of the Sun at the end of the Sun path, below the horizon of the Earth (or any other astronomical object in the Solar System) due to its Earth's rotation, rotation. As viewed from everywhere on Earth, it ...
* Sun transit time
References
{{DEFAULTSORT:Solar Elevation Angle Horizontal coordinate system Sun Solar energy