Soddy Circle

In geometry, Descartes' theorem states that for every four kissing, or mutually tangent circles, the radii of the circles satisfy a certain quadratic equation. By solving this equation, one can construct a fourth circle tangent to three given, mutually tangent circles. The theorem is named after René Descartes, who stated it in 1643.

Frederick Soddy's 1936 poem ''The Kiss Precise'' summarizes the theorem in terms of the ''bends'' (signed inverse radii) of the four circles:

Special cases of the theorem apply when one or two of the circles is replaced by a straight line (with zero bend) or when the bends are integers or square numbers. A version of the theorem using complex numbers allows the centers of the circles, and not just their radii, to be calculated. With an appropriate definition of curvature, the theorem also applies in spherical geometry and hyperbolic geometry. In higher dimensions, an analogous quadratic equation applies to systems of pairwise tangent spheres or hyperspheres.

History

Geometrical problems involving tangent circles have been pondered for millennia. In ancient Greece of the third century BC, Apollonius of Perga devoted an entire book to the topic, 'Tangencies'' It has been lost, and is known largely through a description of its contents by Pappus of Alexandria and through fragmentary references to it in medieval Islamic mathematics. However, Greek geometry was largely focused on straightedge and compass construction. For instance, the problem of Apollonius, closely related to Descartes' theorem, asks for the construction of a circle tangent to three given circles which need not themselves be tangent. Instead, Descartes' theorem is formulated using algebraic relations between numbers describing geometric forms. This is characteristic of analytic geometry, a field pioneered by René Descartes and Pierre de Fermat in the first half of the 17th century.

Descartes discussed the tangent circle problem briefly in 1643, in two letters to Princess Elisabeth of the Palatinate. Descartes initially posed to the princess the problem of Apollonius. After Elisabeth's partial results revealed that solving the full problem analytically would be too tedious, he simplified the problem to the case in which the three given circles are mutually tangent, and in solving this simplified problem he came up with the equation describing the relation between the radii, or curvatures, of four pairwise tangent circles. This result became known as Descartes' theorem. Descartes did not provide the reasoning through which he found this relation.

Japanese mathematics frequently concerned problems involving circles and their tangencies, and Japanese mathematician Yamaji Nushizumi stated a form of Descartes' circle theorem in 1751. Like Descartes, he expressed it as a polynomial equation on the radii rather than their curvatures. The special case of this theorem for one straight line and three circles was recorded on a Japanese sangaku tablet from 1824.

Descartes' theorem was rediscovered in 1826 by Jakob Steiner, in 1842 by Philip Beecroft, and in 1936 by Frederick Soddy. Soddy chose to format his version of the theorem as a poem, ''The Kiss Precise'', and published it in ''Nature''. The kissing circles in this problem are sometimes known as Soddy circles. Soddy also extended the theorem to spheres, and in another poem described the chain of six spheres each tangent to its neighbors and to three given mutually tangent spheres, a configuration now called Soddy's hexlet. Thorold Gosset and several others extended the theorem and the poem to arbitrary dimensions; Gosset's version was published the following year. The generalization is sometimes called the ''Soddy–Gosset theorem'', although both the hexlet and the three-dimensional version were known earlier, in sangaku and in the 1886 work of Robert Lachlan. A generalization for multiple kissing circles in two dimensions was proved in 2025.

Multiple proofs of the theorem have been published. Steiner's proof uses Pappus chains and Viviani's theorem. Proofs by Philip Beecroft and by H. S. M. Coxeter involve four more circles, passing through triples of tangencies of the original three circles; Coxeter also provided a proof using inversive geometry. Additional proofs involve arguments based on symmetry, calculations in exterior algebra, or algebraic manipulation of Heron's formula (for which see ). The result also follows from the observation that the Cayley–Menger determinant of the four coplanar circle centers is zero.

Statement

Descartes' theorem is most easily stated in terms of the circles' curvatures. The ''signed curvature'' (or ''bend'') of a circle is defined where $r$ is its radius. The larger a circle, the smaller is the magnitude of its curvature, and vice versa. The sign in $k=\pm1/r$ (represented by the $\pm$ symbol) is positive for a circle that is ''externally'' tangent to the other circles. For an ''internally'' tangent circle that ''circumscribes'' the other circles, the sign is negative. If a straight line is considered a degenerate circle with zero curvature (and thus infinite radius), Descartes' theorem also applies to a line and three circles that are all three mutually tangent (see Generalized circle).

For four circles that are tangent to each other at six distinct points, with curvatures $k_i$ Descartes' theorem says:

If one of the four curvatures is considered to be a variable, and the rest to be constants, this is a quadratic equation.
To find the radius of a fourth circle tangent to three given kissing circles, the quadratic equation can be solved as

The $\pm$ symbol indicates that in general this equation has ''two'' solutions, and any triple of tangent circles has two tangent circles (or degenerate straight lines). Problem-specific criteria may favor one of these two solutions over the other in any given problem.

The theorem does not apply to systems of circles with more than two circles tangent to each other at the same point. It requires that the points of tangency be distinct. When more than two circles are tangent at a single point, there can be infinitely many such circles, with arbitrary curvatures; see pencil of circles.

Locating the circle centers

To determine a circle completely, not only its radius (or curvature), but also its center must be known. The relevant equation is expressed most clearly if the Cartesian coordinates $(x,y)$ are interpreted as a complex number $z=x+iy$. The equation then looks similar to Descartes' theorem and is therefore called the ''complex Descartes theorem''. Given four circles with curvatures $k_i$ and centers $z_i$ the following equality holds in addition to :

Once $k_4$ has been found using , one may proceed to calculate $z_4$ by solving as a quadratic equation, leading to a form similar to :

$z_4 = \frac.$

Again, in general there are two solutions corresponding to the two solutions The plus/minus sign in the above formula does not necessarily correspond to the plus/minus sign in the formula

Special cases

Three congruent circles

When three of the four circles are congruent, their centers form an equilateral triangle, as do their points of tangency. The two possibilities for a fourth circle tangent to all three are concentric, and reduces to

$k_4 = (3 \pm2 \sqrt)k_1.$

One or more straight lines

If one of the three circles is replaced by a straight line tangent to the remaining circles, then its curvature is zero and drops out of For instance, then can be factorized

\begin
& \bigl(\sqrt + \sqrt + \sqrt\bigr)
\bigl(\bigr) \\ mu& \quad \cdot
\bigl(\sqrt + \sqrt - \sqrt\bigr)
\bigl(\sqrt + \sqrt - \sqrt\bigr) = 0,
\end

and simplifies

$k_4=k_1+k_2\pm2\sqrt.$

Taking the square root of both sides leads to another alternative formulation of this case

$\sqrt=\sqrt\pm \sqrt,$

which has been described as "a sort of demented version of the Pythagorean theorem".

If two circles are replaced by lines, the tangency between the two replaced circles becomes a parallelism between their two replacement lines. In this case, is reduced to the trivial

$\displaystyle k_4=k_1.$

This corresponds to the observation that, for all four curves to remain mutually tangent, the other two circles must be

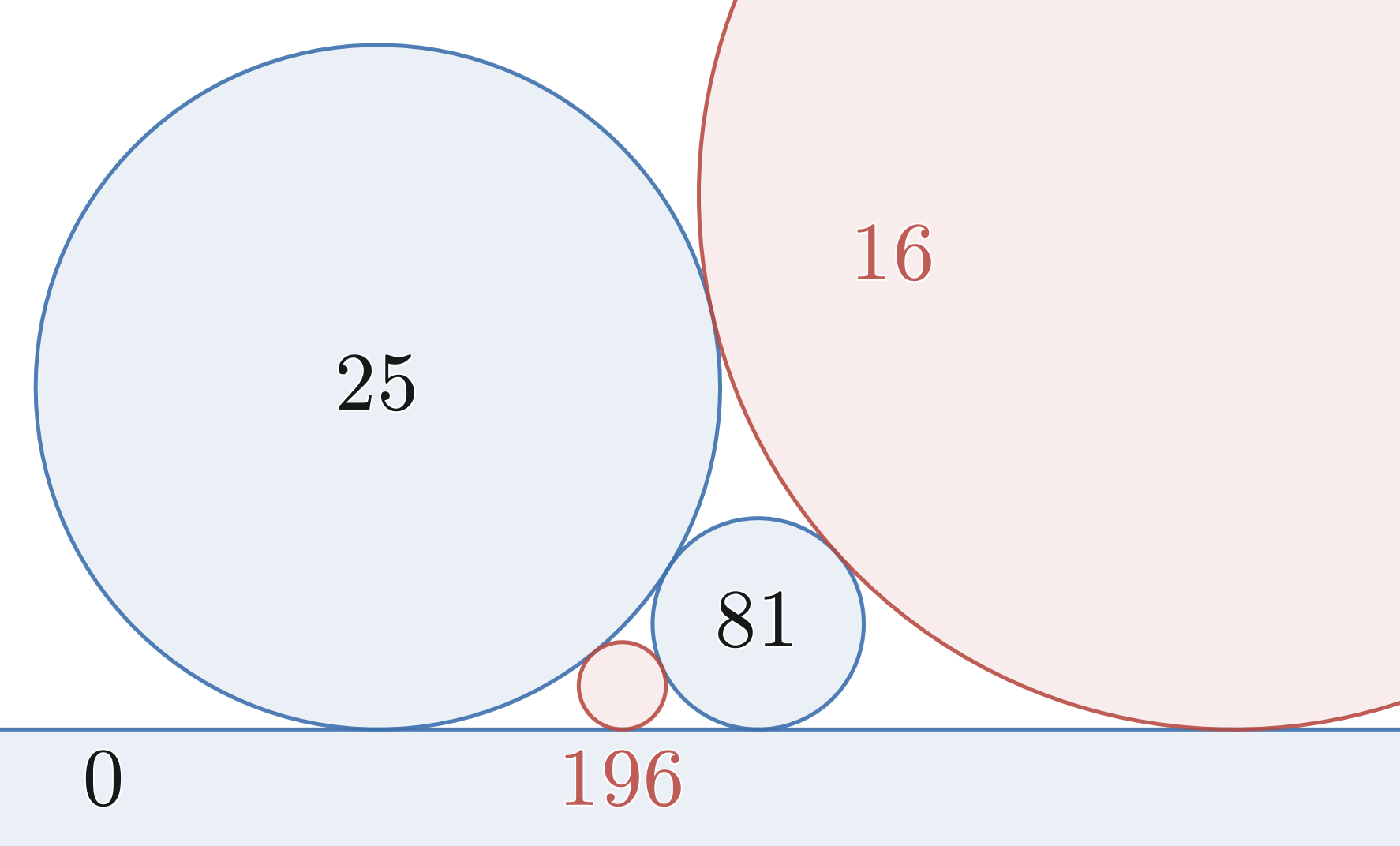
Integer curvatures

When four tangent circles described by all have integer curvatures, the alternative fourth circle described by the second solution to the equation must also have an integer curvature. This is because both solutions differ from an integer by the square root of an integer, and so either solution can only be an integer if this square root, and hence the other solution, is also an integer. Every four integers that satisfy the equation in Descartes' theorem form the curvatures of four tangent Integer quadruples of this type are also closely related to Heronian triangles, triangles with integer sides and

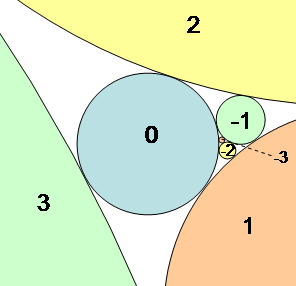
Starting with any four mutually tangent circles, and repeatedly replacing one of the four with its alternative solution ( Vieta jumping), in all possible ways, leads to a system of infinitely many tangent circles called an Apollonian gasket. When the initial four circles have integer curvatures, so does each replacement, and therefore all of the circles in the gasket have integer curvatures. Any four tangent circles with integer curvatures belong to exactly one such gasket, uniquely described by its ''root quadruple'' of the largest four largest circles and four smallest curvatures. This quadruple can be found, starting from any other quadruple from the same gasket, by repeatedly replacing the smallest circle by a larger one that solves the same Descartes equation, until no such reduction is possible.

A root quadruple is said to be ''primitive'' if it has no nontrivial common divisor. Every primitive root quadruple can be found from a factorization of a sum of two squares, as the To be primitive, it must satisfy the additional Factorizations of sums of two squares can be obtained using the sum of two squares theorem. Any other integer Apollonian gasket can be formed by multiplying a primitive root quadruple by an arbitrary integer, and any quadruple in one of these gaskets (that is, any integer solution to the Descartes equation) can be formed by reversing the replacement process used to find the root quadruple. For instance, the gasket with root shown in the figure, is generated in this way from the factorized sum of two squares

Ford circles

The special cases of one straight line and integer curvatures combine in the Ford circles. These are an infinite family of circles tangent to the of the Cartesian coordinate system at its rational points. Each fraction $p/q$ (in lowest terms) has a circle tangent to the line at the point $(p/q,0)$ with curvature $2q^2$. Three of these curvatures, together with the zero curvature of the axis, meet the conditions of Descartes' theorem whenever the denominators of two of the corresponding fractions sum to the denominator of the third. The two Ford circles for fractions $p/q$ and $r/s$ (both in lowest terms) are tangent When they are tangent, they form a quadruple of tangent circles with the and with the circle for their mediant $(p+r)/(q+s)$.

The Ford circles belong to a special Apollonian gasket with root bounded between two parallel lines, which may be taken as the and the This is the only Apollonian gasket containing a straight line, and not bounded within a negative-curvature circle. The Ford circles are the circles in this gasket that are tangent to the .

Geometric progression

When the four radii of the circles in Descartes' theorem are assumed to be in a geometric progression with the curvatures are also in the same progression (in reverse). Plugging this ratio into the theorem gives the equation

$2(1+\rho^2+\rho^4+\rho^6)=(1+\rho+\rho^2+\rho^3)^2,$

which has only one real solution greater than one, the ratio

$\rho=\varphi + \sqrt \approx 2.89005 \ ,$

where $\varphi$ is the golden ratio. If the same progression is continued in both directions, each consecutive four numbers describe circles obeying Descartes' theorem. The resulting double-ended geometric progression of circles can be arranged into a single spiral pattern of tangent circles, called Coxeter's loxodromic sequence of tangent circles. It was first described, together with analogous constructions in higher dimensions, by H. S. M. Coxeter in 1968.

Soddy circles of a triangle

Any triangle in the plane has three externally tangent circles centered at its vertices. Letting $A, B, C$ be the three points, $a, b, c$ be the lengths of the opposite sides, and $s = \tfrac12(a + b + c)$ be the semiperimeter, these three circles have radii By Descartes' theorem, two more circles, sometimes called ''Soddy circles'', are tangent to these three circles. They are separated by the incircle, one interior to it and one Descartes' theorem can be used to show that the inner Soddy circle's curvature where $\Delta$ is the triangle's area, $R$ is its circumradius, and $r$ is its inradius. The outer Soddy circle has curvature The inner curvature is always positive, but the outer curvature can be positive, negative, or zero. Triangles whose outer circle degenerates to a straight line with curvature zero have been called "Soddyian triangles".

One of the many proofs of Descartes' theorem is based on this connection to triangle geometry and on Heron's formula for the area of a triangle as a function of its side lengths.
If three circles are externally tangent, with radii $r_1, r_2, r_3,$ then their centers $P_1, P_2, P_3$ form the vertices of a triangle with side lengths $r_1+r_2,$ $r_1+r_3,$ and $r_2+r_3,$ and semiperimeter $r_1+r_2+r_3.$ By Heron's formula, this triangle $\triangle P_1P_2P_3$ has area

$\sqrt.$

Now consider the inner Soddy circle with radius $r_4,$ centered at point $P_4$ inside the triangle. Triangle $\triangle P_1P_2P_3$ can be broken into three smaller triangles $\triangle P_1P_2P_4,$ $\triangle P_4P_2P_3,$ and $\triangle P_1P_4P_3,$ whose areas can be obtained by substituting $r_4$ for one of the other radii in the area formula above. The area of the first triangle equals the sum of these three areas:

$\begin \sqrt = & \sqrt+\\ &\sqrt+\\ &\sqrt. \end$

Careful algebraic manipulation shows that this formula is equivalent to , Descartes' theorem.

This analysis covers all cases in which four circles are externally tangent; one is always the inner Soddy circle of the other three. The cases in which one of the circles is internally tangent to the other three and forms their outer Soddy circle are similar. Again the four centers $P_1, P_2, P_3, P_4$ form four triangles, but (letting $P_4$ be the center of the outer Soddy circle) the triangle sides incident to $P_4$ have lengths that are differences of radii, $r_4 - r_1,$ $r_4 - r_1,$ and $r_4 - r_3,$ rather than sums. $P_4$ may lie inside or outside the triangle formed by the other three centers; when it is inside, this triangle's area equals the sum of the other three triangle areas, as above. When it is outside, the quadrilateral formed by the four centers can be subdivided by a diagonal into two triangles, in two different ways, giving an equality between the sum of two triangle areas and the sum of the other two triangle areas. In every case, the area equation reduces to Descartes' theorem. This method does not apply directly to the cases in which one of the circles degenerates to a line, but those can be handled as a limiting case of circles.

Generalizations

Arbitrary four-circle configurations

Descartes' theorem can be expressed as a matrix equation and then generalized to other configurations of four oriented circles by changing the matrix. Let $\mathbf$ be a column vector of the four circle curvatures and let $\mathbf$ be a symmetric matrix whose coefficients $q_$ represent the relative orientation between the th and th oriented circles at their intersection point:
$\mathbf = \begin \phantom1 & -1 & -1 & -1 \\ -1 & \phantom1 & -1 & -1 \\ -1 & -1 & \phantom1 & -1 \\ -1 & -1 & -1 & \phantom1 \\ \end, \qquad \mathbf^ = \frac14 \begin \phantom1 & -1 & -1 & -1 \\ -1 & \phantom1 & -1 & -1 \\ -1 & -1 & \phantom1 & -1 \\ -1 & -1 & -1 & \phantom1 \\ \end.$

Then can be rewritten as the matrix equation

$\mathbf^\mathsf\mathbf^\mathbf = 0.$

As a generalization of Descartes' theorem, a modified symmetric matrix $\mathbf$ can represent any desired configuration of four circles by replacing each coefficient with the ''inclination'' $q_$ between two circles, defined as

$q_ = \frac,$

where $r_i, r_j$ are the respective radii of the circles, and $d_$ is the Euclidean distance between their centers. When the circles intersect, the cosine of the intersection angle between the circles. The inclination, sometimes called inversive distance, is $1$ when the circles are tangent and oriented the same way at their point of tangency, $-1$ when the two circles are tangent and oriented oppositely at the point of tangency, $0$ for orthogonal circles, outside the interval $$1, 1/math> for non-intersecting circles, and $\infty$ in the limit as one circle degenerates to a

The equation $\mathbf^\mathsf\mathbf^\mathbf = 0$ is satisfied for any arbitrary configuration of four circles in the plane, provided $\mathbf$ is the appropriate matrix of pairwise inclinations.

Spherical and hyperbolic geometry

Descartes' theorem generalizes to mutually tangent great or small circles in spherical geometry if the curvature of the $j$th circle is defined as $k_j = \cot \rho_j,$ the geodesic curvature of the circle relative to the sphere, which equals the cotangent of the oriented intrinsic radius $\rho_j.$ Then:

$(k_1 + k_2 + k_3+k_4)^2 = 2(k_1^2+k_2^2+k_3^2+k_4^2) + 4.$

Solving for one of the curvatures in terms of the other three,

$k_4 = k_1 + k_2 + k_3 \pm2 \sqrt.$

As a matrix equation,

$\mathbf^\mathsf\mathbf^\mathbf = -1.$

The quantity $1/k_j = \tan \rho_j$ is the "stereographic diameter" of a small circle. This is the Euclidean length of the diameter in the stereographically projected plane when some point on the circle is projected to the origin. For a great circle, such a stereographic projection is a straight line through the origin, so $k_j = 0$.

Likewise, the theorem generalizes to mutually tangent circles in hyperbolic geometry if the curvature of the $j$th cycle is defined as $k_j = \coth \rho_j,$ the geodesic curvature of the circle relative to the hyperbolic plane, the hyperbolic cotangent of the oriented intrinsic radius $\rho_j.$ Then:

$(k_1 + k_2 + k_3+k_4)^2 = 2(k_1^2+k_2^2+k_3^2+k_4^2) - 4.$

Solving for one of the curvatures in terms of the other three,

$k_4 = k_1 + k_2 + k_3 \pm2 \sqrt.$

As a matrix equation,

$\mathbf^\mathsf\mathbf^\mathbf = 1.$

This formula also holds for mutually tangent configurations in hyperbolic geometry including hypercycles and horocycles, if $k_j$ is the geodesic curvature of the cycle relative to the hyperbolic plane, the reciprocal of the stereographic diameter of the cycle. This is the diameter under stereographic projection (the Poincaré disk model) when one endpoint of the diameter is projected to the origin. Hypercycles do not have a well-defined center or intrinsic radius and horocycles have an ideal point for a center and infinite intrinsic radius, but $, k_j, > 1$ for a hyperbolic circle, $, k_j, = 1$ for a horocycle, $, k_j, < 1$ for a hypercycle, and $k_j = 0$ for a geodesic.

Higher dimensions

In $n$-dimensional Euclidean space, the maximum number of mutually tangent hyperspheres is $n+2$. For example, in 3-dimensional space, five spheres can be mutually tangent. The curvatures of the hyperspheres satisfy

$\biggl(\sum_^ k_i\biggr)^ = n\,\sum_^ k_i^2$

with the case $k_i=0$ corresponding to a flat hyperplane, generalizing the 2-dimensional version of the theorem. Although there is no 3-dimensional analogue of the complex numbers, the relationship between the positions of the centers can be re-expressed as a matrix equation, which also generalizes to $n$ dimensions.

In three dimensions, suppose that three mutually tangent spheres are fixed, and a fourth sphere $S_1$ is given, tangent to the three fixed spheres. The three-dimensional version of Descartes' theorem can be applied to find a sphere $S_2$ tangent to $S_1$ and the fixed spheres, then applied again to find a new sphere $S_3$ tangent to $S_2$ and the fixed spheres, and so on. The result is a cyclic sequence of six spheres each tangent to its neighbors in the sequence and to the three fixed spheres, a configuration called Soddy's hexlet, after Soddy's discovery and publication of it in the form of another poem in 1936.

Higher-dimensional configurations of mutually tangent hyperspheres in spherical or hyperbolic geometry, with curvatures defined as above, satisfy

$\biggl(\sum_^ k_i\biggr)^ = nC + n\,\sum_^ k_i^2,$

where $C = 2$ in spherical geometry and $C = -2$ in hyperbolic geometry.

See also

* Circle packing in a circle
* Euler's four-square identity
* Malfatti circles

References

Further reading

* {{citation
, last1 = Maehara , first1 = Hiroshi
, last2 = Martini , first2 = Horst
, year = 2024
, chapter = Chapter 2: Bend Formulas
, pages = 31–48
, title = Circles, Spheres and Spherical Geometry
, publisher = Birkhäuser
, doi = 10.1007/978-3-031-62776-7_2
, isbn = 978-3-031-62775-0

Euclidean plane geometry
Theorems about circles
Analytic geometry
Circle packing