Sinhc Re Plot

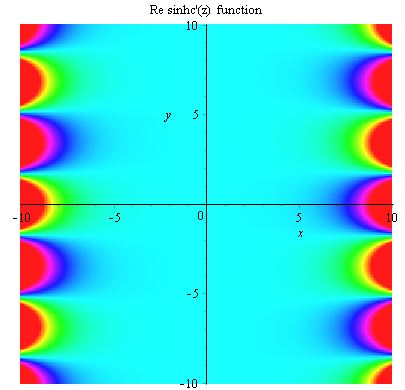
In mathematics, the sinhc function appears frequently in papers about optical scattering, Heisenberg spacetime and hyperbolic geometry. For $z \neq 0$, it is defined as
$\operatorname(z)=\frac$

The sinhc function is the hyperbolic analogue of the sinc function, defined by $\sin x/x$. It is a solution of the following differential equation:
$w(z) z-2\,\frac w (z) -z \frac w (z) =0$

Properties

The first-order derivative is given by
:$\frac - \frac$
The Taylor series expansion is$\sum_^\infty \frac.$The Padé approximant is$\operatorname \left( z \right) = \left( 1+ \,^+\,^+\,^+\,^ \right) \left( 1-\,^+\,^-\,^ +\,^ \right) ^$

In terms of other special functions

* $\operatorname(z)=\frac$, where $(a,b,z)$ is Kummer's confluent hypergeometric function.
* $\operatorname(z)=\frac$, where $(q, \alpha, \gamma, \delta, \epsilon ,z)$ is the biconfluent Heun function.
* $\operatorname(z)=1/2\,\frac$, where $(a,b,z)$ is a Whittaker function.

Gallery

{,
,
,
,

See also

*Tanc function
*Tanhc function
*Sinhc integral
*Coshc function

References

Special functions