Set Estimation on:
[Wikipedia]
[Google]
[Amazon]
In
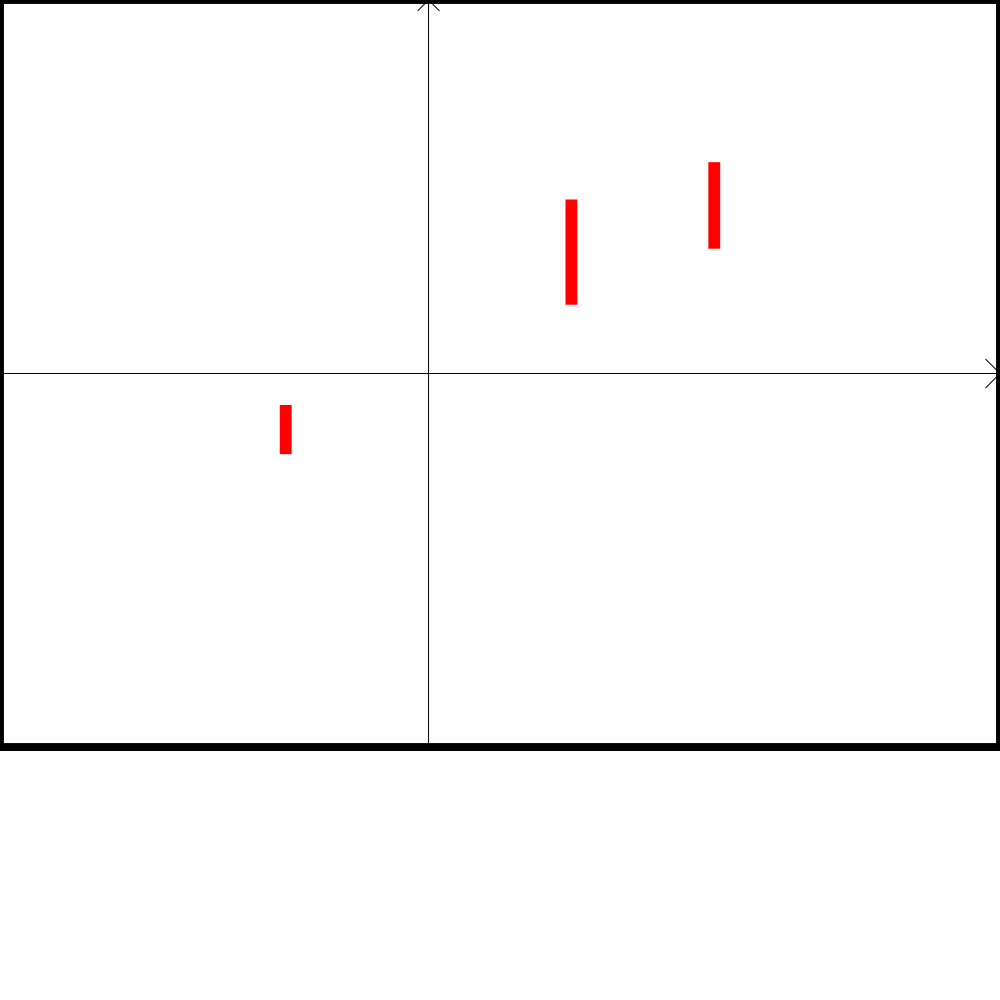 Assume that at times , , ,
the following interval measurements have been collected:
as illustrated by Figure 1. The corresponding measurement set (here a box) is
The model function is defined by
The components of are obtained using the model for each time measurement.
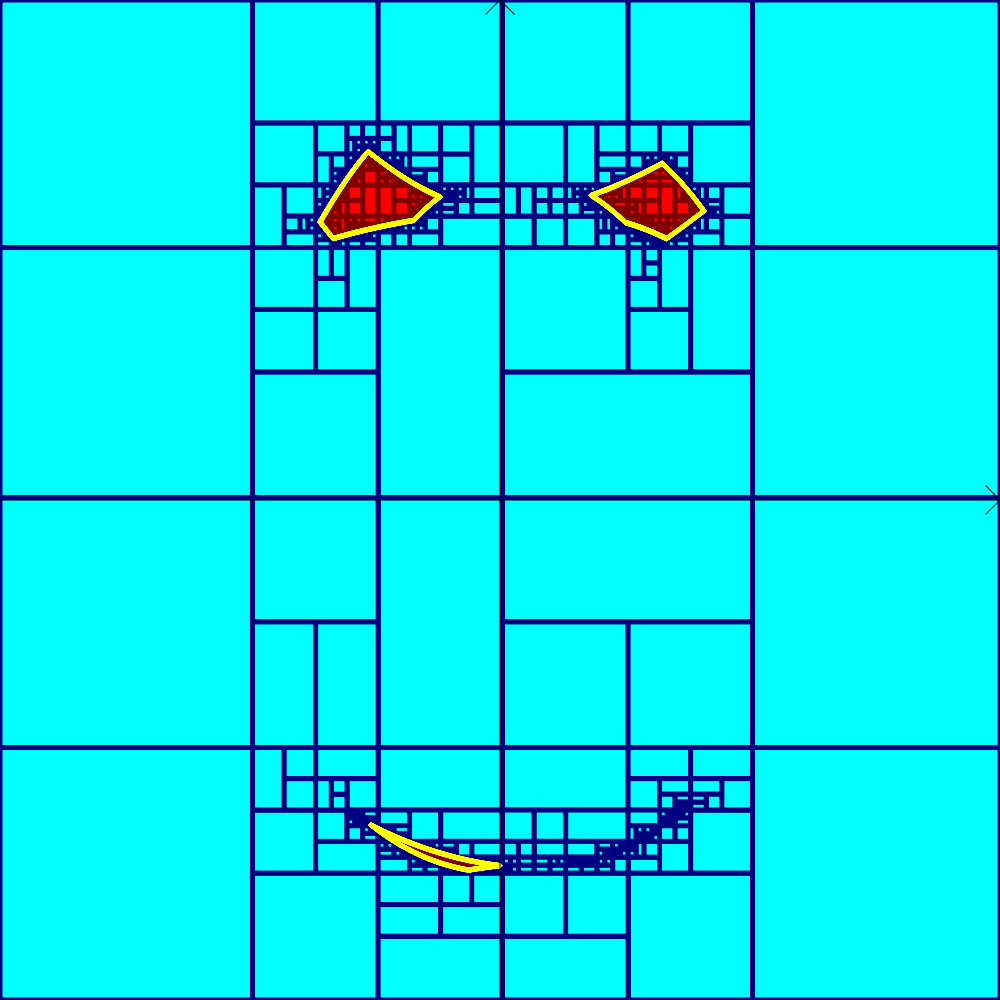
After solving the set inversion problem, we get the approximation depicted on Figure 2.
Red boxes are inside the feasible set and blue boxes are outside .
Assume that at times , , ,
the following interval measurements have been collected:
as illustrated by Figure 1. The corresponding measurement set (here a box) is
The model function is defined by
The components of are obtained using the model for each time measurement.
After solving the set inversion problem, we get the approximation depicted on Figure 2.
Red boxes are inside the feasible set and blue boxes are outside .
statistics
Statistics (from German language, German: ', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a s ...
, a random vector
In probability, and statistics, a multivariate random variable or random vector is a list or vector of mathematical variables each of whose value is unknown, either because the value has not yet occurred or because there is imperfect knowledge ...
is classically represented by a probability density function
In probability theory, a probability density function (PDF), density function, or density of an absolutely continuous random variable, is a Function (mathematics), function whose value at any given sample (or point) in the sample space (the s ...
.
In a set-membership approach or set estimation, is represented by a set to which is assumed to belong. This means that the support
Support may refer to:
Arts, entertainment, and media
* Supporting character
* Support (art), a solid surface upon which a painting is executed
Business and finance
* Support (technical analysis)
* Child support
* Customer support
* Income Su ...
of the probability distribution
In probability theory and statistics, a probability distribution is a Function (mathematics), function that gives the probabilities of occurrence of possible events for an Experiment (probability theory), experiment. It is a mathematical descri ...
function of is included inside . On the one hand, representing random vectors by sets makes it possible to provide fewer assumptions on the random variables (such as independence
Independence is a condition of a nation, country, or state, in which residents and population, or some portion thereof, exercise self-government, and usually sovereignty, over its territory. The opposite of independence is the status of ...
) and dealing with nonlinearities is easier. On the other hand, a probability distribution function provides a more accurate information than a set enclosing its support.
Set-membership estimation
Set membership estimation (or ''set estimation'' for short) is an estimation approach which considers that measurements are represented by a set (most of the time a box of where is the number of measurements) of the measurement space. If is the parameter vector and is the model function, then the set of all feasible parameter vectors is where is the prior set for the parameters. Characterizing corresponds to a set-inversion problem.Resolution
When is linear the feasible set can be described by linear inequalities and can be approximated usinglinear programming
Linear programming (LP), also called linear optimization, is a method to achieve the best outcome (such as maximum profit or lowest cost) in a mathematical model whose requirements and objective are represented by linear function#As a polynomia ...
techniques.
When is nonlinear, the resolution can be performed using interval analysis. The feasible set
In mathematical optimization and computer science, a feasible region, feasible set, or solution space is the set of all possible points (sets of values of the choice variables) of an optimization problem that satisfy the problem's constraints, ...
is then approximated by an inner and an outer subpavings. The main limitation of the method is its exponential complexity with respect to the number of parameters.
Example
Consider the following model where and are the two parameters to be estimated. Assume that at times , , ,
the following interval measurements have been collected:
as illustrated by Figure 1. The corresponding measurement set (here a box) is
The model function is defined by
The components of are obtained using the model for each time measurement.
After solving the set inversion problem, we get the approximation depicted on Figure 2.
Red boxes are inside the feasible set and blue boxes are outside .
Assume that at times , , ,
the following interval measurements have been collected:
as illustrated by Figure 1. The corresponding measurement set (here a box) is
The model function is defined by
The components of are obtained using the model for each time measurement.
After solving the set inversion problem, we get the approximation depicted on Figure 2.
Red boxes are inside the feasible set and blue boxes are outside .

Recursive case
Set estimation can be used to estimate the state of a system described by state equations using a recursive implementation. When the system is linear, the corresponding feasible set for the state vector can be described by polytopes or by ellipsoids . When the system is nonlinear, the set can be enclosed by subpavings.Robust case
When outliers occur, the set estimation method generally returns an empty set. This is due to the fact that the intersection between sets of parameter vectors that are consistent with the th data bar is empty. To be robust with respect to outliers, we generally characterize the set of parameter vectors that are consistent with all data bars except of them. This is possible using the notion of -relaxed intersection The ''relaxed intersection'' of ''m'' sets corresponds to the classical
intersection between sets except that it is allowed to relax few sets in order to avoid an empty intersection.
This notion can be used to solve Constraint satisfaction problem, ...
.
See also
*Set identification In statistics and econometrics, set identification (or partial identification) extends the concept of identifiability (or "point identification") in statistical models to environments where the model and the distribution of observable variables are ...
References
{{Reflist, 2 Estimation theory