sensitivity index

The sensitivity index or discriminability index or detectability index is a dimensionless statistic used in signal detection theory. A higher index indicates that the signal can be more readily detected.

Definition

The discriminability index is the separation between the means of two distributions (typically the signal and the noise distributions), in units of the standard deviation.

Equal variances/covariances

For two univariate distributions $a$ and $b$ with the same standard deviation, it is denoted by $d'$ ('dee-prime'):
: $d' = \frac$.

In higher dimensions, i.e. with two multivariate distributions with the same variance-covariance matrix $\mathbf$, (whose symmetric square-root, the standard deviation matrix, is $\mathbf$), this generalizes to the Mahalanobis distance between the two distributions:
: $d'=\sqrt = \lVert \mathbf^(\boldsymbol_a-\boldsymbol_b) \rVert = \lVert \boldsymbol_a-\boldsymbol_b \rVert /\sigma_$,
where $\sigma_ = 1/ \lVert\mathbf^\boldsymbol\rVert$ is the 1d slice of the sd along the unit vector $\boldsymbol$ through the means, i.e. the $d'$ equals the $d'$ along the 1d slice through the means.

For two bivariate distributions with equal variance-covariance, this is given by:

: $^2 =\frac \left(^2_x+^2_y-2\rho _x _y \right)$,

where $\rho$ is the correlation coefficient, and here $d'_x=\frac$ and $d'_y=\frac$, i.e. including the signs of the mean differences instead of the absolute.

$d'$ is also estimated as $Z(\text)-Z(\text)$.

Unequal variances/covariances

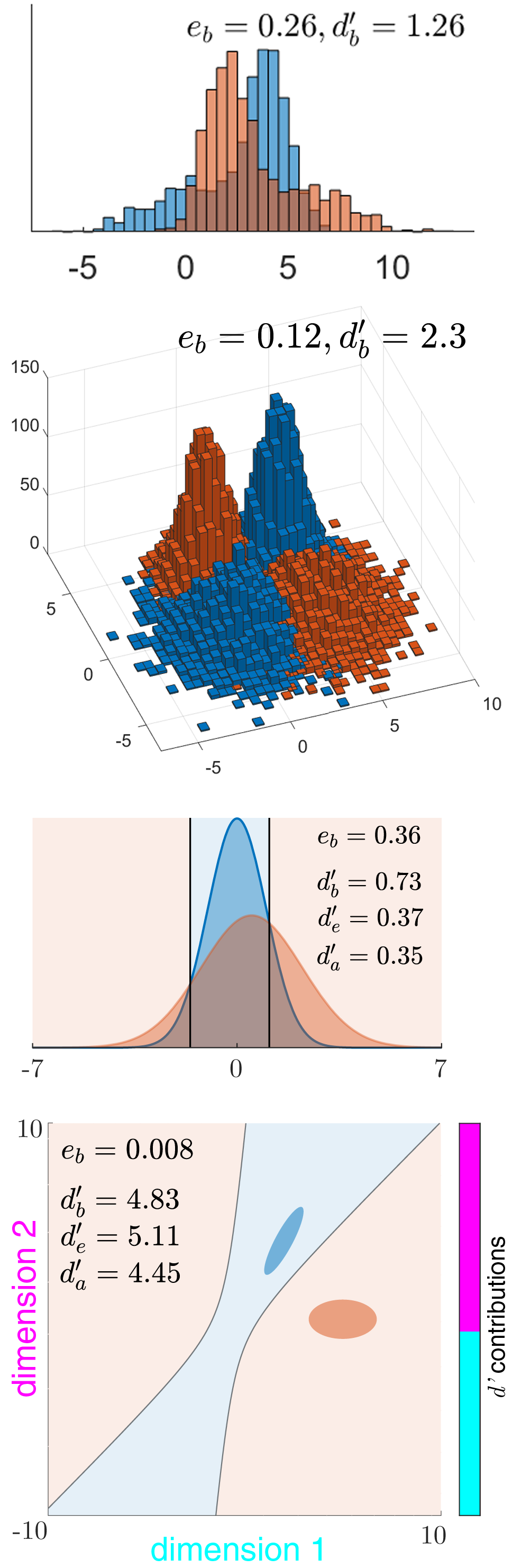
When the two distributions have different standard deviations (or in general dimensions, different covariance matrices), there exist several contending indices, all of which reduce to $d'$ for equal variance/covariance.

Bayes discriminability index

This is the maximum (Bayes-optimal) discriminability index for two distributions, based on the amount of their overlap, i.e. the optimal (Bayes) error of classification $e_b$ by an ideal observer, or its complement, the optimal accuracy $a_b$:
: $d'_b=-2Z\left(\text e_b\right)=2Z\left(\text a_b\right)$,
where $Z$ is the inverse cumulative distribution function of the standard normal. The Bayes discriminability between univariate or multivariate normal distributions can be numerically computed
Matlab code
, and may also be used as an approximation when the distributions are close to normal.

$d'_b$ is a positive-definite statistical distance measure that is free of assumptions about the distributions, like the Kullback-Leibler divergence $D_\text$. $D_\text(a,b)$ is asymmetric, whereas $d'_b(a,b)$ is symmetric for the two distributions. However, $d'_b$ does not satisfy the triangle inequality, so it is not a full metric.

In particular, for a yes/no task between two univariate normal distributions with means $\mu_a,\mu_b$ and variances $v_a>v_b$, the Bayes-optimal classification accuracies are:

: $p(A, a)=p(^2_ > v_b c), \; \; p(B, b)=p(^2_ < v_a c)$,

where $\chi'^2$ denotes the non-central chi-squared distribution, $\lambda=\left(\frac\right)^2$, and $c=\lambda+\frac$. The Bayes discriminability $d'_b=2Z\left(\frac \right).$

$d'_b$ can also be computed from the ROC curve of a yes/no task between two univariate normal distributions with a single shifting criterion. It can also be computed from the ROC curve of any two distributions (in any number of variables) with a shifting likelihood-ratio, by locating the point on the ROC curve that is farthest from the diagonal.

For a two-interval task between these distributions, the optimal accuracy is $a_b=p \left( \tilde^2_>0 \right)$ ($\tilde^2$ denotes the generalized chi-squared distribution), where
$\boldsymbol=\begin \sigma_s^2 & -\sigma_n^2 \end, \; \boldsymbol=\begin 1 & 1 \end, \; \boldsymbol=\frac \begin \sigma_s^2 & \sigma_n^2 \end$. The Bayes discriminability $d'_b=2Z\left(a_b\right)$.

RMS sd discriminability index

A common approximate (i.e. sub-optimal) discriminability index that has a closed-form is to take the average of the variances, i.e. the rms of the two standard deviations: $d'_a=\left\vert \mu_a -\mu_b \right\vert/\sigma_\text$ (also denoted by $d_a$). It is $\sqrt$ times the $z$-score of the area under the receiver operating characteristic curve (AUC) of a single-criterion observer. This index is extended to general dimensions as the Mahalanobis distance using the pooled covariance, i.e. with \mathbf_\text=\left left(\mathbf_a+\mathbf_b\right)/2 \right\frac as the common sd matrix.

Average sd discriminability index

Another index is $d'_e=\left\vert \mu_a -\mu_b \right\vert/\sigma_\text$, extended to general dimensions using $\mathbf_\text=\left(\mathbf_a+\mathbf_b\right)/2$ as the common sd matrix.

Comparison of the indices

It has been shown that for two univariate normal distributions, $d'_a \leq d'_e \leq d'_b$, and for multivariate normal distributions, $d'_a \leq d'_e$ still.

Thus, $d'_a$ and $d'_e$ underestimate the maximum discriminability $d'_b$ of univariate normal distributions. $d'_a$ can underestimate $d'_b$ by a maximum of approximately 30%. At the limit of high discriminability for univariate normal distributions, $d'_e$ converges to $d'_b$. These results often hold true in higher dimensions, but not always. Simpson and Fitter promoted $d'_a$ as the best index, particularly for two-interval tasks, but Das and Geisler have shown that $d'_b$ is the optimal discriminability in all cases, and $d'_e$ is often a better closed-form approximation than $d'_a$, even for two-interval tasks.

The approximate index $d'_$, which uses the geometric mean of the sd's, is less than $d'_b$ at small discriminability, but greater at large discriminability.

Contribution to discriminability by each dimension

In general, the contribution to the total discriminability by each dimension or feature may be measured using the amount by which the discriminability drops when that dimension is removed. If the total Bayes discriminability is $d'$ and the Bayes discriminability with dimension $i$ removed is $d'_$, we can define the contribution of dimension $i$ as $\sqrt$. This is the same as the individual discriminability of dimension $i$ when the covariance matrices are equal and diagonal, but in the other cases, this measure more accurately reflects the contribution of a dimension than its individual discriminability.

Scaling the discriminability of two distributions

We may sometimes want to scale the discriminability of two data distributions by moving them closer or farther apart. One such case is when we are modeling a detection or classification task, and the model performance exceeds that of the subject or observed data. In that case, we can move the model variable distributions closer together so that it matches the observed performance, while also predicting which specific data points should start overlapping and be misclassified.

There are several ways of doing this. One is to compute the mean vector and covariance matrix of the two distributions, then effect a linear transformation to interpolate the mean and sd matrix (square root of the covariance matrix) of one of the distributions towards the other.

Another way that is by computing the decision variables of the data points (log likelihood ratio that a point belongs to one distribution vs another) under a multinormal model, then moving these decision variables closer together or farther apart.

See also

* Receiver operating characteristic (ROC)
* Summary statistics
* Effect size

References

*

External links

Interactive signal detection theory tutorial
including calculation of ''d''′.

Detection theory
Signal processing
Summary statistics

{{stat-stub