Self Avoiding Walk

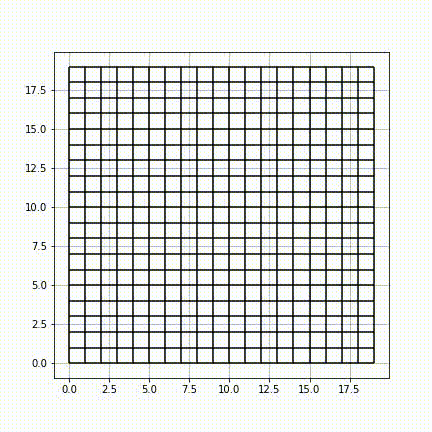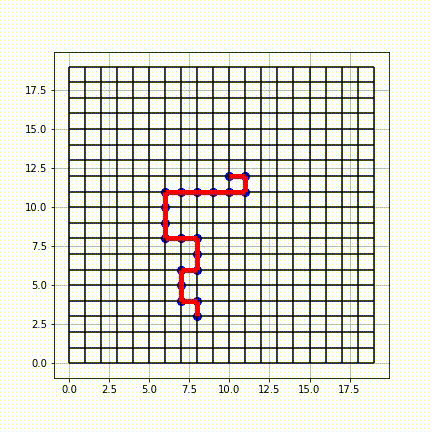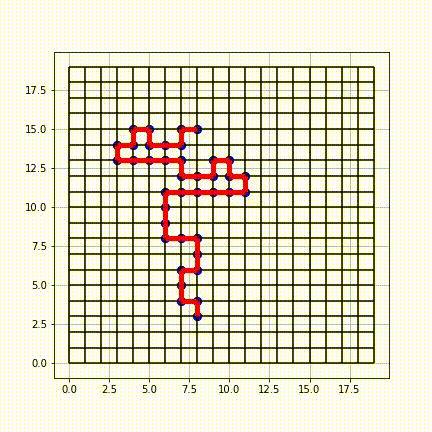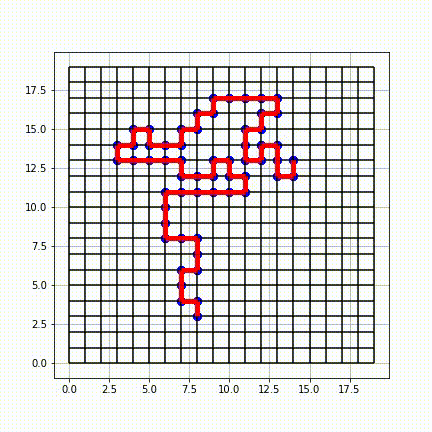In mathematics, a self-avoiding walk (SAW) is a sequence of moves on a lattice (a lattice path) that does not visit the same point more than once. This is a special case of the graph theoretical notion of a path. A self-avoiding polygon (SAP) is a closed self-avoiding walk on a lattice. Very little is known rigorously about the self-avoiding walk from a mathematical perspective, although physicists have provided numerous conjectures that are believed to be true and are strongly supported by numerical simulations.

In computational physics, a self-avoiding walk is a chain-like path in or with a certain number of nodes, typically a fixed step length and has the property that it doesn't cross itself or another walk. A system of SAWs satisfies the so-called excluded volume condition. In higher dimensions, the SAW is believed to behave much like the ordinary random walk.

SAWs and SAPs play a central role in the modeling of the topological and knot-theoretic behavior of thread- and loop-like molecules such as proteins. Indeed, SAWs may have first been introduced by the chemist Paul Flory in order to model the real-life behavior of chain-like entities such as solvents and polymers, whose physical volume prohibits multiple occupation of the same spatial point.

SAWs are fractals. For example, in the fractal dimension is 4/3, for it is close to 5/3 while for the fractal dimension is . The dimension is called the upper critical dimension above which excluded volume is negligible. A SAW that does not satisfy the excluded volume condition was recently studied to model explicit surface geometry resulting from expansion of a SAW.

The properties of SAWs cannot be calculated analytically, so numerical simulations are employed. The pivot algorithm is a common method for Markov chain Monte Carlo simulations for the uniform measure on -step self-avoiding walks. The pivot algorithm works by taking a self-avoiding walk and randomly choosing a point on this walk, and then applying symmetrical transformations (rotations and reflections) on the walk after the th step to create a new walk.

Calculating the number of self-avoiding walks in any given lattice is a common computational problem. There is currently no known formula, although there are rigorous methods of approximation.

Universality

One of the phenomena associated with self-avoiding walks and statistical physics models in general is the notion of universality, that is, independence of macroscopic observables from microscopic details, such as the choice of the lattice. One important quantity that appears in conjectures for universal laws is the connective constant, defined as follows. Let denote the number of -step self-avoiding walks. Since every -step self avoiding walk can be decomposed into an -step self-avoiding walk and an -step self-avoiding walk, it follows that . Therefore, the sequence is subadditive and we can apply Fekete's lemma to show that the following limit exists:

:$\mu = \lim_ c_n^.$

is called the connective constant, since depends on the particular lattice chosen for the walk so does . The exact value of is only known for the hexagonal lattice, found by Stanislav Smirnov and Hugo Duminil-Copin, where it is equal to:

:$\sqrt.$

For other lattices, has only been approximated numerically, and is believed not to even be an algebraic number. It is conjectured that

:$c_n \approx \mu^n n^$

as , where depends on the lattice, but the power law correction $n^$ does not; in other words, this law is believed to be universal.

On networks

Self-avoiding walks have also been studied in the context of network theory. In this context, it is customary to treat the SAW as a dynamical process, such that in every time-step a walker randomly hops between neighboring nodes of the network. The walk ends when the walker reaches a dead-end state, such that it can no longer progress to newly un-visited nodes. It was recently found that on Erdős–Rényi networks, the distribution of path lengths of such dynamically grown SAWs can be calculated analytically, and follows the Gompertz distribution. For arbitrary networks, the distribution of path lengths of the walk, the degree distribution of the non-visited network and the first-hitting-time distribution to a node can be obtained by solving a set of coupled recurrence equations.

Limits

Consider the uniform measure on -step self-avoiding walks in the full plane. It is currently unknown whether the limit of the uniform measure as induces a measure on infinite full-plane walks. However, Harry Kesten has shown that such a measure exists for self-avoiding walks in the half-plane. One important question involving self-avoiding walks is the existence and conformal invariance of the scaling limit, that is, the limit as the length of the walk goes to infinity and the mesh of the lattice goes to zero. The scaling limit of the self-avoiding walk is conjectured to be described by Schramm–Loewner evolution with parameter

See also

*
*
*
*
*
*
* Space-filling curves – All are self-avoiding.

References

Further reading

#
#
#
#

External links

*—the number of self-avoiding paths joining opposite corners of an ''N'' × ''N'' grid, for ''N'' from 0 to 12. Also includes an extended list up to ''N'' = 21.
*
Java applet of a 2D self-avoiding walkGeneric python implementation to simulate SAWs and expanding FiberWalks on a square lattices in n-dimensions.
to generate SAWs on the Diamond cubic.

{{Stochastic processes

Polygons
Discrete geometry
Computational physics
Computational chemistry
Variants of random walks