Schönhardt Polyhedron

In geometry, a Schönhardt polyhedron is a polyhedron with the same combinatorial structure as a regular octahedron, but with dihedral angles that are non-convex along three disjoint edges. Because it has no interior diagonals, it cannot be triangulated into tetrahedra without adding new vertices. It has the fewest vertices of any polyhedron that cannot be triangulated. It is named after the German mathematician Erich Schönhardt, who described it in 1928, although the artist Karlis Johansons had exhibited a related structure in 1921.

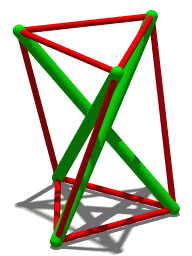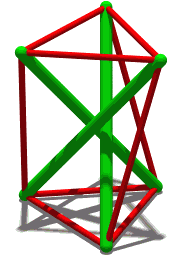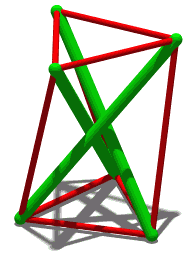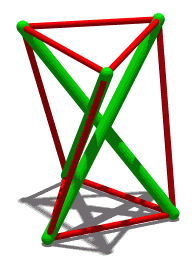
One construction for the Schönhardt polyhedron starts with a triangular prism and twists the two equilateral triangle faces of the prism relative to each other, breaking each square face into two triangles separated by a non-convex edge. Some twist angles produce a ''jumping polyhedron'' whose two solid forms share the same face shapes. A 30° twist instead produces a ''shaky polyhedron'', rigid but not infinitesimally rigid, whose edges form a tensegrity prism.

Schönhardt polyhedra have been used as gadgets in a proof that testing whether a polyhedron has a triangulation is NP-complete. Several other polyhedra, including Jessen's icosahedron, share with the Schönhardt polyhedron the properties of having no triangulation, of jumping or being shaky, or of forming a tensegrity structure.

Construction

One way of constructing a Schönhardt polyhedron starts with a triangular prism, with two parallel equilateral triangles as its faces. One of the triangles is rotated
around the centerline of the prism. The rotation angle is an arbitrary parameter, which can be varied continuously. This rotation causes the square faces of the triangle to become skew polygons, each of which can be re-triangulated with two triangles to form either a convex or a non-convex dihedral angle. When all three of these pairs of triangles are chosen to have a non-convex dihedral, the Schönhardt polyhedron is the result.

Properties

A Schönhardt polyhedron has six vertices, twelve edges, and eight triangular faces. Its six vertices form fifteen unordered pairs. Twelve of these fifteen pairs form edges of the polyhedron: there are six edges in the two equilateral triangle faces, and six edges connecting the two triangles. The remaining three pairs form diagonals of the polyhedron, but lie entirely outside the polyhedron.

The convex hull of the Schönhardt polyhedron is another polyhedron with the same six vertices, and a different set of twelve edges and eight triangular faces. Both this hull, and the Schönhardt polyhedron itself, are combinatorially equivalent to a regular octahedron. The symmetric difference of the hull and the Schönhardt polyhedron consists of three tetrahedra, each lying between one of the concave dihedral edges of the Schönhardt polyhedron and one of the exterior diagonals. Thus, the Schönhardt polyhedron can be formed by removing these three tetrahedra from a convex (but irregular) octahedron.

Impossibility of triangulation

A triangulation of a polyhedron is a partition into tetrahedra, meeting face-to-face and using only the vertices of the given polyhedron. Every convex polyhedron has a triangulation in this sense, but the Schönhardt polyhedron does not. Among polyhedra with no triangulation, it has the fewest vertices.

More strongly, no tetrahedron lies entirely inside the Schönhardt polyhedron and shares all four vertices with it. This follows from the following two properties of the Schönhardt
*Every triangle formed by its edges is one of its faces. Therefore, because it is not a tetrahedron itself, every tetrahedron formed by four of its vertices must have an edge that it does not share with the Schönhardt polyhedron.
*Every diagonal that connects two of its vertices but is not an edge of the Schönhardt polyhedron lies outside the polyhedron. Therefore, every tetrahedron that uses such a diagonal as one of its edges must also lie in part outside the Schönhardt polyhedron.

Stability

Some instances of the Schönhardt polyhedron form a ''jumping polyhedron'': a polyhedron that has two different rigid states, both having the same face shapes and the same orientation (convex or concave) of each edge. A model whose surface is made of a stiff but somewhat deformable material, such as cardstock, can be made to "jump" between the two shapes. A solid model could not change shape in this way. Neither could a model made of a more rigid material like glass: although it could exist in either of the two shapes, it would be unable to deform sufficiently to move between them. This stands in contrast to Cauchy's rigidity theorem, according to which, for each convex polyhedron, there is no other polyhedron having the same face shapes and edge orientations.

In his original work on this polyhedron, Schönhardt noted a related property: in one special form, when the two equilateral faces are twisted at an angle of 30° with respect to each other, this polyhedron becomes ''shaky'': rigid with respect to continuous motion, but not infinitesimally rigid. At this same rotation angle of 30°, the edges of the Schönhardt polyhedron can be used to form a tensegrity structure called the ''tensegrity prism'', with compression elements for its non-convex edges and tension elements for its convex edges. The discovery of this form as a tensegrity structure rather than as a polyhedron has been credited to Latvian-Soviet artist Karlis Johansons in 1921, a few years before the work of Schönhardt.

Applications

used Schönhardt's polyhedron as the basis for a proof that it is NP-complete to determine whether a non-convex polyhedron can be triangulated. The proof uses many copies of the Schönhardt polyhedron, with its top face removed, as gadgets within a larger polyhedron. Any triangulation of the overall polyhedron must include a tetrahedron connecting the bottom face of each gadget to a vertex in the rest of the polyhedron that can see this bottom face. The complex pattern of obstructions between tetrahedra of this type can be used to simulate Boolean logic components in a reduction from the Boolean satisfiability problem.

Related constructions

Schönhardt's 1928 discovery of this polyhedron was prompted by earlier work of Nels Johann Lennes, who published in 1911 a seven-vertex polyhedron with no triangulation.

As well as jumping, non-convex polyhedra can be flexible, having a continuous family of shapes with the same faces. The Bricard octahedra are flexible in this way, with the same combinatorial structure as the Schönhardt polyhedron, but unlike the Schönhardt polyhedron they are self-intersecting.

It was shown by that the Schönhardt polyhedron can be generalized to other polyhedra, combinatorially equivalent to antiprisms, that cannot be triangulated. These polyhedra are formed by connecting regular in two parallel planes, twisted with respect to each other, in such a way that $k$ of the $2k$ edges that connect the two have concave dihedrals. For sufficiently small twisting angles, the result has no triangulation. Another polyhedron that cannot be triangulated is Jessen's icosahedron, which is combinatorially equivalent to a regular icosahedron, and (like the tensegrity form of Schönhardt's polyhedron) also a shaky tensegrity.

In a different direction, constructed a family of polyhedra that share with the Schönhardt polyhedron the property that there are no internal diagonals. The tetrahedron and the Császár polyhedron have no diagonals at all: every pair of vertices in these polyhedra forms an edge. It remains an open question whether there are any other polyhedra (with manifold boundary) without diagonals, although there exist non-manifold surfaces with no diagonals and any number of vertices greater than five.

References

External links

Schönhardt polyhedron
mathgrrl, including links to a free 3d-printable model

{{DEFAULTSORT:Schonhardt polyhedron
Nonconvex polyhedra
1928 introductions
Science and technology in Germany