Scale Height on:
[Wikipedia]
[Google]
[Amazon]
 In atmospheric,
In atmospheric,
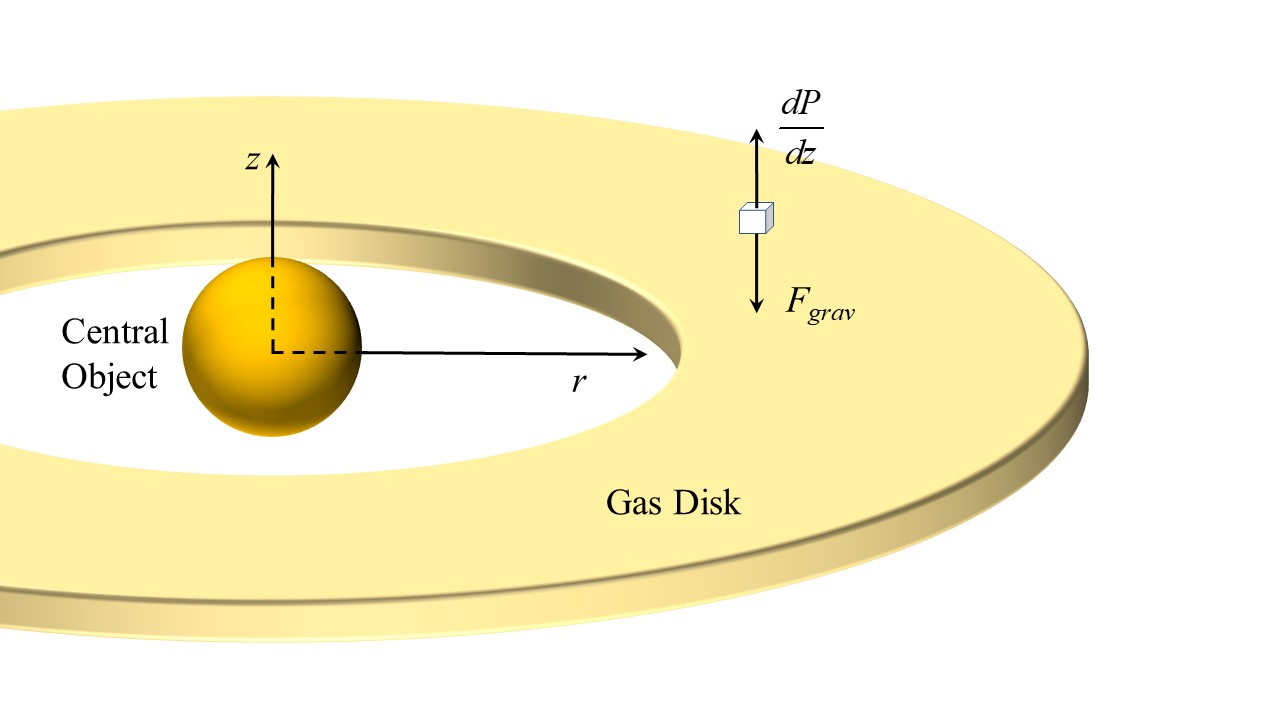 For a disk of gas around a condensed central object, such as, for example, a protostar, one can derive a disk scale height which is somewhat analogous to the planetary scale height. We start with a disc of gas that has a mass small relative to the central object. We assume that the disc is in hydrostatic equilibrium with the ''z'' component of gravity from the star, where the gravity component is pointing to the midplane of the disk:
where
: ''G'' = Newtonian constant of gravitation ≈
: ''r'' = the radial cylindrical coordinate for the distance from the center of the star or centrally condensed object
: ''z'' = the height/altitude cylindrical coordinate for the distance from the disk midplane (or center of the star)
: ''M''* = the mass of the star/centrally condensed object
: ''P'' = the pressure of the gas in the disk
: = the gas mass density in the disk
In the thin disk approximation, , and the hydrostatic equilibrium, the equation is
To determine the gas pressure, one can use the
For a disk of gas around a condensed central object, such as, for example, a protostar, one can derive a disk scale height which is somewhat analogous to the planetary scale height. We start with a disc of gas that has a mass small relative to the central object. We assume that the disc is in hydrostatic equilibrium with the ''z'' component of gravity from the star, where the gravity component is pointing to the midplane of the disk:
where
: ''G'' = Newtonian constant of gravitation ≈
: ''r'' = the radial cylindrical coordinate for the distance from the center of the star or centrally condensed object
: ''z'' = the height/altitude cylindrical coordinate for the distance from the disk midplane (or center of the star)
: ''M''* = the mass of the star/centrally condensed object
: ''P'' = the pressure of the gas in the disk
: = the gas mass density in the disk
In the thin disk approximation, , and the hydrostatic equilibrium, the equation is
To determine the gas pressure, one can use the
earth
Earth is the third planet from the Sun and the only astronomical object known to Planetary habitability, harbor life. This is enabled by Earth being an ocean world, the only one in the Solar System sustaining liquid surface water. Almost all ...
, and planetary sciences, a scale height, usually denoted by the capital letter ''H'', is a distance ( vertical or radial) over which a physical quantity
A physical quantity (or simply quantity) is a property of a material or system that can be Quantification (science), quantified by measurement. A physical quantity can be expressed as a ''value'', which is the algebraic multiplication of a ''nu ...
decreases by a factor of e (the base of natural logarithms, approximately 2.718).
Scale height used in a simple atmospheric pressure model
For planetary atmospheres, scale height is the increase in altitude for which theatmospheric pressure
Atmospheric pressure, also known as air pressure or barometric pressure (after the barometer), is the pressure within the atmosphere of Earth. The standard atmosphere (symbol: atm) is a unit of pressure defined as , which is equivalent to 1,013. ...
decreases by a factor of ''e''. The scale height remains constant for a particular temperature. It can be calculated by
or equivalently,
where
: ''k''B = Boltzmann constant
The Boltzmann constant ( or ) is the proportionality factor that relates the average relative thermal energy of particles in a ideal gas, gas with the thermodynamic temperature of the gas. It occurs in the definitions of the kelvin (K) and the ...
=
: ''R'' = molar gas constant = 8.31446 J⋅K−1⋅mol−1
: ''T'' = mean atmospheric temperature
Temperature is a physical quantity that quantitatively expresses the attribute of hotness or coldness. Temperature is measurement, measured with a thermometer. It reflects the average kinetic energy of the vibrating and colliding atoms making ...
in kelvins = 250 K for Earth
: ''m'' = mean mass of a molecule
: ''M'' = mean molar mass
In chemistry, the molar mass () (sometimes called molecular weight or formula weight, but see related quantities for usage) of a chemical substance ( element or compound) is defined as the ratio between the mass () and the amount of substance ...
of atmospheric particles = 0.029 kg/mol for Earth
: ''g'' = acceleration
In mechanics, acceleration is the Rate (mathematics), rate of change of the velocity of an object with respect to time. Acceleration is one of several components of kinematics, the study of motion. Accelerations are Euclidean vector, vector ...
due to gravity
In physics, gravity (), also known as gravitation or a gravitational interaction, is a fundamental interaction, a mutual attraction between all massive particles. On Earth, gravity takes a slightly different meaning: the observed force b ...
at the current location
The pressure (force per unit area) at a given altitude is a result of the weight of the overlying atmosphere. If at a height of ''z'' the atmosphere has density
Density (volumetric mass density or specific mass) is the ratio of a substance's mass to its volume. The symbol most often used for density is ''ρ'' (the lower case Greek letter rho), although the Latin letter ''D'' (or ''d'') can also be u ...
''ρ'' and pressure ''P'', then moving upwards an infinitesimally small height ''dz'' will decrease the pressure by amount ''dP'', equal to the weight of a layer of atmosphere of thickness ''dz''.
Thus:
where ''g'' is the acceleration due to gravity. For small ''dz'' it is possible to assume ''g'' to be constant; the minus sign indicates that as the height increases the pressure decreases. Therefore, using the equation of state for an ideal gas
An ideal gas is a theoretical gas composed of many randomly moving point particles that are not subject to interparticle interactions. The ideal gas concept is useful because it obeys the ideal gas law, a simplified equation of state, and is ...
of mean molecular mass ''M'' at temperature ''T'', the density can be expressed as
Combining these equations gives
which can then be incorporated with the equation for ''H'' given above to give
which will not change unless the temperature does. Integrating the above and assuming ''P''0 is the pressure at height ''z'' = 0 (pressure at sea level
Mean sea level (MSL, often shortened to sea level) is an mean, average surface level of one or more among Earth's coastal Body of water, bodies of water from which heights such as elevation may be measured. The global MSL is a type of vertical ...
), the pressure at height ''z'' can be written as
This translates as the pressure decreasing exponentially with height.
In Earth's atmosphere, the pressure at sea level ''P''0 averages about , the mean molecular mass of dry air is , and hence ''m'' = × = . As a function of temperature, the scale height of Earth's atmosphere is therefore ''H''/''T'' = ''k''B/''mg'' = / ( × ) = . This yields the following scale heights for representative air temperatures:
: ''T'' = 290 K, ''H'' = 8500 m,
: ''T'' = 273 K, ''H'' = 8000 m,
: ''T'' = 260 K, ''H'' = 7610 m,
: ''T'' = 210 K, ''H'' = 6000 m.
These figures should be compared with the temperature and density of Earth's atmosphere plotted at NRLMSISE-00, which shows the air density dropping from 1200 g/m3 at sea level to 0.125 g/m3 at 70 km, a factor of 9600, indicating an average scale height of 70 / ln(9600) = 7.64 km, consistent with the indicated average air temperature over that range of close to 260 K.
Note:
* Density is related to pressure by the ideal gas
An ideal gas is a theoretical gas composed of many randomly moving point particles that are not subject to interparticle interactions. The ideal gas concept is useful because it obeys the ideal gas law, a simplified equation of state, and is ...
laws. Therefore, density will also decrease exponentially with height from a sea-level value of ''ρ''0 roughly equal to .
* At an altitude over 100 km, the atmosphere is no longer well-mixed, and each chemical species has its own scale height.
* Here temperature and gravitational acceleration were assumed to be constant, but both may vary over large distances.
Planetary examples
Approximate atmospheric scale heights for selected Solar System bodies:Scale height for a thin disk
 For a disk of gas around a condensed central object, such as, for example, a protostar, one can derive a disk scale height which is somewhat analogous to the planetary scale height. We start with a disc of gas that has a mass small relative to the central object. We assume that the disc is in hydrostatic equilibrium with the ''z'' component of gravity from the star, where the gravity component is pointing to the midplane of the disk:
where
: ''G'' = Newtonian constant of gravitation ≈
: ''r'' = the radial cylindrical coordinate for the distance from the center of the star or centrally condensed object
: ''z'' = the height/altitude cylindrical coordinate for the distance from the disk midplane (or center of the star)
: ''M''* = the mass of the star/centrally condensed object
: ''P'' = the pressure of the gas in the disk
: = the gas mass density in the disk
In the thin disk approximation, , and the hydrostatic equilibrium, the equation is
To determine the gas pressure, one can use the
For a disk of gas around a condensed central object, such as, for example, a protostar, one can derive a disk scale height which is somewhat analogous to the planetary scale height. We start with a disc of gas that has a mass small relative to the central object. We assume that the disc is in hydrostatic equilibrium with the ''z'' component of gravity from the star, where the gravity component is pointing to the midplane of the disk:
where
: ''G'' = Newtonian constant of gravitation ≈
: ''r'' = the radial cylindrical coordinate for the distance from the center of the star or centrally condensed object
: ''z'' = the height/altitude cylindrical coordinate for the distance from the disk midplane (or center of the star)
: ''M''* = the mass of the star/centrally condensed object
: ''P'' = the pressure of the gas in the disk
: = the gas mass density in the disk
In the thin disk approximation, , and the hydrostatic equilibrium, the equation is
To determine the gas pressure, one can use the ideal gas law
The ideal gas law, also called the general gas equation, is the equation of state of a hypothetical ideal gas. It is a good approximation of the behavior of many gases under many conditions, although it has several limitations. It was first stat ...
:
with
: ''T'' = the gas temperature in the disk, where the temperature is a function of ''r'', but independent of ''z''
: = the mean molecular mass of the gas
Using the ideal gas law
The ideal gas law, also called the general gas equation, is the equation of state of a hypothetical ideal gas. It is a good approximation of the behavior of many gases under many conditions, although it has several limitations. It was first stat ...
and the hydrostatic equilibrium equation, gives
which has the solution
where is the gas mass density at the midplane of the disk at a distance ''r'' from the center of the star, and is the disk scale height with
with the solar mass, the astronomical unit
The astronomical unit (symbol: au or AU) is a unit of length defined to be exactly equal to . Historically, the astronomical unit was conceived as the average Earth-Sun distance (the average of Earth's aphelion and perihelion), before its m ...
, and the dalton.
As an illustrative approximation, if we ignore the radial variation in the temperature , we see that and that the disk increases in altitude as one moves radially away from the central object.
Due to the assumption that the gas temperature ''T'' in the disk is independent of ''z'', is sometimes known as the isothermal disk scale height.
Disk scale height in a magnetic field
Amagnetic field
A magnetic field (sometimes called B-field) is a physical field that describes the magnetic influence on moving electric charges, electric currents, and magnetic materials. A moving charge in a magnetic field experiences a force perpendicular ...
in a thin gas disk around a central object can change the scale height of the disk. For example, if a non-perfectly conducting disk is rotating through a poloidal magnetic field (i.e., the initial magnetic field is perpendicular to the plane of the disk), then a toroidal (i.e., parallel to the disk plane) magnetic field will be produced within the disk, which will ''pinch'' and compress the disk. In this case, the gas density of the disk is
where the ''cut-off'' density has the form
where
: is the permeability of free space
: is the electrical conductivity
Electrical resistivity (also called volume resistivity or specific electrical resistance) is a fundamental specific property of a material that measures its electrical resistance or how strongly it resists electric current. A low resistivity in ...
of the disk
: is the magnetic flux density of the poloidal field in the direction
: is the rotational angular velocity of the central object (if the poloidal magnetic field is independent of the central object, then can be set to zero)
: is the keplerian angular velocity of the disk at a distance from the central object.
These formulae give the maximum height of the magnetized disk as
while the e-folding magnetic scale height is
See also
*Time constant
In physics and engineering, the time constant, usually denoted by the Greek language, Greek letter (tau), is the parameter characterizing the response to a step input of a first-order, LTI system theory, linear time-invariant (LTI) system.Concre ...
References
{{reflist Atmospheric dynamics Vertical position