Saros Series on:
[Wikipedia]
[Google]
[Amazon]
The saros () is a period of exactly 223 synodic months, approximately 6585.3211 days, or 18 years, 10, 11, or 12 days (depending on the number of leap years), and 8 hours, that can be used to predict eclipses of the Sun and
 The Saros period of 223 lunar months (in
The Saros period of 223 lunar months (in
 After one saros, the Moon will have completed roughly an integer number of synodic, draconic, and anomalistic periods (223, 242, and 239) and the Earth-Sun-Moon geometry will be nearly identical: the Moon will have the same phase and be at the same node and the same distance from the Earth. In addition, because the saros is close to 18 years in length (about 11 days longer), the Earth will be nearly the same distance from the Sun, and tilted to it in nearly the same orientation (same season). Given the date of an eclipse, one saros later a nearly identical eclipse can be predicted. During this 18-year period, about 40 other solar and lunar eclipses take place, but with a somewhat different geometry. One saros equaling 18.03 years is not equal to a perfect integer number of lunar orbits (Earth revolutions with respect to the fixed stars of 27.32166 days sidereal month), therefore, even though the relative geometry of the Earth–Sun–Moon system will be nearly identical after a saros, the Moon will be in a slightly different position with respect to the stars for each eclipse in a saros series. The axis of rotation of the Earth–Moon system exhibits a
After one saros, the Moon will have completed roughly an integer number of synodic, draconic, and anomalistic periods (223, 242, and 239) and the Earth-Sun-Moon geometry will be nearly identical: the Moon will have the same phase and be at the same node and the same distance from the Earth. In addition, because the saros is close to 18 years in length (about 11 days longer), the Earth will be nearly the same distance from the Sun, and tilted to it in nearly the same orientation (same season). Given the date of an eclipse, one saros later a nearly identical eclipse can be predicted. During this 18-year period, about 40 other solar and lunar eclipses take place, but with a somewhat different geometry. One saros equaling 18.03 years is not equal to a perfect integer number of lunar orbits (Earth revolutions with respect to the fixed stars of 27.32166 days sidereal month), therefore, even though the relative geometry of the Earth–Sun–Moon system will be nearly identical after a saros, the Moon will be in a slightly different position with respect to the stars for each eclipse in a saros series. The axis of rotation of the Earth–Moon system exhibits a
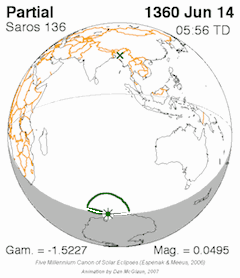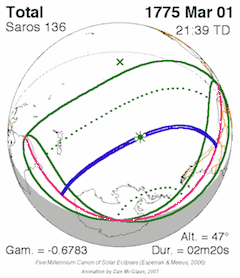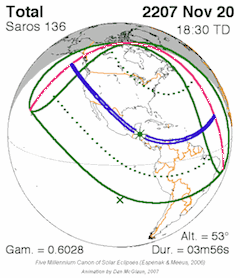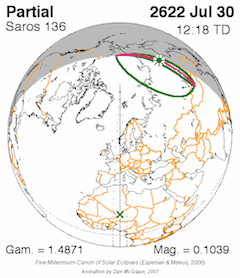 Each saros series starts with a partial eclipse (Sun first enters the end of the node), and each successive saros the path of the Moon is shifted either northward (when near the descending node) or southward (when near the ascending node) due to the fact that the saros is not an exact integer of draconic months (about one hour short). At some point, eclipses are no longer possible and the series terminates (Sun leaves the beginning of the node). An arbitrary solar saros series was designated as solar saros series 1 by compilers of eclipse statistics. This series has finished, but the eclipse of November 16, 1990 BC (
Each saros series starts with a partial eclipse (Sun first enters the end of the node), and each successive saros the path of the Moon is shifted either northward (when near the descending node) or southward (when near the ascending node) due to the fact that the saros is not an exact integer of draconic months (about one hour short). At some point, eclipses are no longer possible and the series terminates (Sun leaves the beginning of the node). An arbitrary solar saros series was designated as solar saros series 1 by compilers of eclipse statistics. This series has finished, but the eclipse of November 16, 1990 BC (
''Canon der Finsternisse''
Vienna * Jean Meeus, ''Mathematical Astronomy Morsels'', Willmann-Bell, Inc., 1997 (Chapter 9, p. 51, Table 9. A Some eclipse Periodicities)
List of all active saros cycles
– Interactive eclipse search
Eclipse Search
– Search 5,000 years of eclipse data by various attributes
– Fundamental astronomy of eclipses {{DEFAULTSORT:Saros cycle 1st-millennium BC introductions Eclipses Time in astronomy Technical factors of astrology Neo-Babylonian Empire Chaldea
Moon
The Moon is Earth's only natural satellite. It is the fifth largest satellite in the Solar System and the largest and most massive relative to its parent planet, with a diameter about one-quarter that of Earth (comparable to the width ...
. One saros period after an eclipse, the Sun, Earth
Earth is the third planet from the Sun and the only astronomical object known to harbor life. While large volumes of water can be found throughout the Solar System, only Earth sustains liquid surface water. About 71% of Earth's surf ...
, and Moon return to approximately the same relative geometry, a near straight line, and a nearly identical eclipse will occur, in what is referred to as an eclipse cycle
Eclipses may occur repeatedly, separated by certain intervals of time: these intervals are called eclipse cycles. The series of eclipses separated by a repeat of one of these intervals is called an eclipse series.
Eclipse conditions
Eclips ...
. A sar is one half of a saros.
A series of eclipses that are separated by one saros is called a ''saros series''. It corresponds to:
*6,585.321347 solar days
*18.029 year
A year or annus is the orbital period of a planetary body, for example, the Earth, moving in its orbit around the Sun. Due to the Earth's axial tilt, the course of a year sees the passing of the seasons, marked by change in weather, the ...
s
*223 synodic months
*241.999 draconic months
*18.999 eclipse years (38 eclipse seasons)
*238.992 anomalistic months
The 19 eclipse years means that if there is a solar eclipse
A solar eclipse occurs when the Moon passes between Earth and the Sun, thereby obscuring the view of the Sun from a small part of the Earth, totally or partially. Such an alignment occurs during an eclipse season, approximately every six mo ...
(or lunar eclipse), then after one saros a new moon will take place at the same node of the orbit of the Moon, and under these circumstances another eclipse can occur.
History
The earliest discovered historical record of what is known as the saros is byChaldean
Chaldean (also Chaldaean or Chaldee) may refer to:
Language
* an old name for the Aramaic language, particularly Biblical Aramaic
* Chaldean Neo-Aramaic, a modern Aramaic language
* Chaldean script, a variant of the Syriac alphabet
Places
* Chal ...
(neo-Babylonian) astronomers in the last several centuries BC. It was later known to Hipparchus, Pliny and Ptolemy
Claudius Ptolemy (; grc-gre, Πτολεμαῖος, ; la, Claudius Ptolemaeus; AD) was a mathematician, astronomer, astrologer, geographer, and music theorist, who wrote about a dozen scientific treatises, three of which were of import ...
.
The name "saros" ( el, σάρος) was applied to the eclipse cycle by Edmond Halley in 1686, who took it from the '' Suda'', a Byzantine
The Byzantine Empire, also referred to as the Eastern Roman Empire or Byzantium, was the continuation of the Roman Empire primarily in its eastern provinces during Late Antiquity and the Middle Ages, when its capital city was Constantin ...
lexicon of the 11th century. The Suda says, " he saros isa measure and a number among Chaldea
Chaldea () was a small country that existed between the late 10th or early 9th and mid-6th centuries BCE, after which the country and its people were absorbed and assimilated into the indigenous population of Babylonia. Semitic-speaking, it was ...
ns. For 120 saroi make 2220 years (years of 12 lunar months) according to the Chaldeans' reckoning, if indeed the saros makes 222 lunar months, which are 18 years and 6 months (i.e. years of 12 lunar months)." The information in the ''Suda'' in turn was derived directly or otherwise from the ''Chronicle'' of Eusebius of Caesarea, which quoted Berossus. ( Guillaume Le Gentil claimed that Halley's usage was incorrect in 1756, but the name continues to be used.) The Greek word apparently comes from the Babylonian word "sāru" meaning the number 3600 or the Greek verb "saro" (σαρῶ) that means sweep (the sky with the series of eclipses).
 The Saros period of 223 lunar months (in
The Saros period of 223 lunar months (in Greek numerals
Greek numerals, also known as Ionic, Ionian, Milesian, or Alexandrian numerals, are a system of writing numbers using the letters of the Greek alphabet. In modern Greece, they are still used for ordinal numbers and in contexts similar to those ...
, ΣΚΓ′) is in the Antikythera Mechanism user manual of this instrument, made around 150 to 100 BC in Greece, as seen in the picture. This number is one of a few inscriptions of the mechanism that are visible with unaided eye. Above it the period of Metonic cycle
The Metonic cycle or enneadecaeteris (from grc, ἐννεακαιδεκαετηρίς, from ἐννεακαίδεκα, "nineteen") is a period of almost exactly 19 years after which the lunar phases recur at the same time of the year. The rec ...
and Callippic cycle are visible too.
Description
The saros, a period of 6585.3211 days (15 common years + 3 leap years + 12.321 days, 14 common years + 4 leap years + 11.321 days, or 13 common years + 5 leap years + 10.321 days), is useful for predicting the times at which nearly identical eclipses will occur. Three periodicities related to lunar orbit, the synodic month, the draconic month, and the anomalistic month coincide almost perfectly each saros cycle. For an eclipse to occur, either the Moon must be located between the Earth and Sun (for asolar eclipse
A solar eclipse occurs when the Moon passes between Earth and the Sun, thereby obscuring the view of the Sun from a small part of the Earth, totally or partially. Such an alignment occurs during an eclipse season, approximately every six mo ...
) or the Earth must be located between the Sun and Moon (for a lunar eclipse). This can happen only when the Moon is new or full
Full may refer to:
* People with the surname Full, including:
** Mr. Full (given name unknown), acting Governor of German Cameroon, 1913 to 1914
* A property in the mathematical field of topology; see Full set
* A property of functors in the mathe ...
, respectively, and repeat occurrences of these lunar phases result from solar and lunar orbits producing the Moon's ''synodic period'' of 29.53059 days. During most full and new moons, however, the shadow of the Earth or Moon falls to the north or south of the other body. Eclipses occur when the three bodies form a nearly straight line. Because the plane of the lunar orbit is inclined to that of the Earth, this condition occurs only when a full or new Moon is near or in the ecliptic plane, that is when the Moon is at one of the two nodes (the ascending or descending node). The period of time for two successive lunar passes through the ecliptic plane (returning to the same node) is termed the ''draconic month'', a 27.21222 day period. The three-dimensional geometry of an eclipse, when the new or full moon is near one of the nodes, occurs every five or six months when the Sun is in conjunction or opposition to the Moon and coincidentally also near a node of the Moon's orbit at that time, or twice per eclipse year. Two eclipses separated by one saros have very similar appearance and duration due to the distance between the Earth and Moon being nearly the same for each event: this is because the saros is also an integer multiple of the ''anomalistic month'' of 27.5545 days, the period of the eccentricity of lunar orbit.
 After one saros, the Moon will have completed roughly an integer number of synodic, draconic, and anomalistic periods (223, 242, and 239) and the Earth-Sun-Moon geometry will be nearly identical: the Moon will have the same phase and be at the same node and the same distance from the Earth. In addition, because the saros is close to 18 years in length (about 11 days longer), the Earth will be nearly the same distance from the Sun, and tilted to it in nearly the same orientation (same season). Given the date of an eclipse, one saros later a nearly identical eclipse can be predicted. During this 18-year period, about 40 other solar and lunar eclipses take place, but with a somewhat different geometry. One saros equaling 18.03 years is not equal to a perfect integer number of lunar orbits (Earth revolutions with respect to the fixed stars of 27.32166 days sidereal month), therefore, even though the relative geometry of the Earth–Sun–Moon system will be nearly identical after a saros, the Moon will be in a slightly different position with respect to the stars for each eclipse in a saros series. The axis of rotation of the Earth–Moon system exhibits a
After one saros, the Moon will have completed roughly an integer number of synodic, draconic, and anomalistic periods (223, 242, and 239) and the Earth-Sun-Moon geometry will be nearly identical: the Moon will have the same phase and be at the same node and the same distance from the Earth. In addition, because the saros is close to 18 years in length (about 11 days longer), the Earth will be nearly the same distance from the Sun, and tilted to it in nearly the same orientation (same season). Given the date of an eclipse, one saros later a nearly identical eclipse can be predicted. During this 18-year period, about 40 other solar and lunar eclipses take place, but with a somewhat different geometry. One saros equaling 18.03 years is not equal to a perfect integer number of lunar orbits (Earth revolutions with respect to the fixed stars of 27.32166 days sidereal month), therefore, even though the relative geometry of the Earth–Sun–Moon system will be nearly identical after a saros, the Moon will be in a slightly different position with respect to the stars for each eclipse in a saros series. The axis of rotation of the Earth–Moon system exhibits a precession
Precession is a change in the orientation of the rotational axis of a rotating body. In an appropriate reference frame it can be defined as a change in the first Euler angle, whereas the third Euler angle defines the rotation itself. In o ...
period of 18.59992 years.
The saros is not an integer number of days, but contains the fraction of of a day. Thus each successive eclipse in a saros series occurs about eight hours later in the day. In the case of an eclipse of the Sun, this means that the region of visibility will shift westward about 120°, or about one third of the way around the globe, and the two eclipses will thus not be visible from the same place on Earth. In the case of an eclipse of the Moon, the next eclipse might still be visible from the same location as long as the Moon is above the horizon. Given three saros eclipse intervals, the local time of day of an eclipse will be nearly the same. This three saros interval (19,755.96 days) is known as a triple saros or '' exeligmos'' ( ''Greek'': "turn of the wheel") cycle.
Saros series
 Each saros series starts with a partial eclipse (Sun first enters the end of the node), and each successive saros the path of the Moon is shifted either northward (when near the descending node) or southward (when near the ascending node) due to the fact that the saros is not an exact integer of draconic months (about one hour short). At some point, eclipses are no longer possible and the series terminates (Sun leaves the beginning of the node). An arbitrary solar saros series was designated as solar saros series 1 by compilers of eclipse statistics. This series has finished, but the eclipse of November 16, 1990 BC (
Each saros series starts with a partial eclipse (Sun first enters the end of the node), and each successive saros the path of the Moon is shifted either northward (when near the descending node) or southward (when near the ascending node) due to the fact that the saros is not an exact integer of draconic months (about one hour short). At some point, eclipses are no longer possible and the series terminates (Sun leaves the beginning of the node). An arbitrary solar saros series was designated as solar saros series 1 by compilers of eclipse statistics. This series has finished, but the eclipse of November 16, 1990 BC (Julian calendar
The Julian calendar, proposed by Roman consul Julius Caesar in 46 BC, was a reform of the Roman calendar. It took effect on , by edict. It was designed with the aid of Greek mathematics, Greek mathematicians and Ancient Greek astronomy, as ...
) for example is in solar saros series 1. There are different saros series for solar and lunar eclipses. For lunar saros series, the lunar eclipse occurring 58.5 synodic months earlier (February 23, 1994 BC) was assigned the number 1. If there is an eclipse one inex
The inex is an eclipse cycle of 10,571.95 days (about 29 years minus 20 days). The cycle was first described in modern times by Crommelin in 1901, but was named by George van den Bergh who studied it in detail half a century later. It has been su ...
(29 years minus about 20 days) after an eclipse of a particular saros series then it is a member of the next series. For example, the eclipse of October 26, 1961 BC is in solar saros series 2. Saros series, of course, went on before these dates, and it is necessary to extend the saros series numbers backwards to negative numbers even just to accommodate eclipses occurring in the years following 2000 BC (up till the last eclipse with a negative saros number in 1367 BC). For solar eclipses the statistics for the complete saros series within the era between 2000 BC and AD 3000 are given in this article's references. It takes between 1226 and 1550 years for the members of a saros series to traverse the Earth's surface from north to south (or vice versa). These extremes allow from 69 to 87 eclipses in each series (most series have 71 or 72 eclipses). From 39 to 59 (mostly about 43) eclipses in a given series will be central (that is, total, annular, or hybrid annular-total). At any given time, approximately 40 different saros series will be in progress.
Saros series, as mentioned, are numbered according to the type of eclipse (lunar or solar). In odd numbered series (for solar eclipses) the Sun is near the ascending node, whereas in even numbered series it is near the descending node (this is reversed for lunar eclipse saros series). Generally, the ordering of these series determines the time at which each series peaks, which corresponds to when an eclipse is closest to one of the lunar nodes. For solar eclipses, the 40 series numbered between 117 117 may refer to:
*117 (number)
*AD 117
*117 BC
*117 (emergency telephone number)
*117 (MBTA bus)
* 117 (TFL bus)
*117 (New Jersey bus)
*''117°'', a 1998 album by Izzy Stradlin
*No. 117 (SPARTAN-II soldier ID), personal name John, the Master Chief ...
and 156
Year 156 ( CLVI) was a leap year starting on Wednesday (link will display the full calendar) of the Julian calendar. At the time, it was known as the Year of the Consulship of Silvanus and Augurinus (or, less frequently, year 909 '' Ab urbe co ...
are active (series 117 will end in 2054), whereas for lunar eclipses, there are now 41 active saros series (these numbers can be derived by counting the number of eclipses listed over an 18-year (saros) period from the eclipse catalog sites).
Example
As an example of a single saros series, this table gives the dates of some of the 72 lunar eclipses for saros series 131. This eclipse series began in AD 1427 with a partial eclipse at the southern edge of the Earth's shadow when the Moon was close to its descending node. In each successive saros, the Moon's orbital path is shifted northward with respect to the Earth's shadow, with the first total eclipse occurring in 1950. For the following 252 years, total eclipses occur, with the central eclipse in 2078. The first partial eclipse after this will occur in the year 2220, and the final partial eclipse of the series will occur in 2707. The total lifetime of lunar saros series 131 is 1280 years. Solar saros 138 interleaves with this lunar saros with an event occurring every 9 years 5 days alternating between each saros series. Because of the fraction of days in a saros, the visibility of each eclipse will differ for an observer at a given locale. For the lunar saros series 131, the first total eclipse of 1950 had its best visibility for viewers in Eastern Europe and the Middle East because mid-eclipse was at 20:44 UT. The following eclipse in the series occurred about 8 hours later in the day with mid-eclipse at 4:47 UT, and was best seen from North America and South America. The third total eclipse occurred about 8 hours later in the day than the second eclipse with mid-eclipse at 12:43 UT, and had its best visibility for viewers in the Western Pacific, East Asia, Australia and New Zealand. This cycle of visibility repeats from the start to the end of the series, with minor variations. Solar saros 138 interleaves with this lunar saros with an event occurring every 9 years 5 days alternating between each saros series. For a similar example for solar saros see solar saros 136.Relationship between lunar and solar saros (sar)
After a given lunar or solar eclipse, after 9 years and days (a half saros, or sar) an eclipse will occur that is lunar instead of solar, or vice versa, with similar properties.Mathematical Astronomy Morsels, Jean Meeus, p.110, Chapter 18, ''The half-saros'' For example, if the Moon's penumbra partially covers the southern limb of the Earth during a solar eclipse, 9 years and days later a lunar eclipse will occur in which the Moon is partially covered by the southern limb of the Earth's penumbra. Likewise, 9 years and days after a total solar eclipse or an annular solar eclipse occurs, a total lunar eclipse will also occur. This 9-year period is referred to as a sar. It includes synodic months, or 111 synodic months plus one fortnight. The fortnight accounts for the alternation between solar and lunar eclipse. For a visual example see '' this chart'' (each row is one sar apart).See also
* List of saros series for lunar eclipses *Eclipse cycle
Eclipses may occur repeatedly, separated by certain intervals of time: these intervals are called eclipse cycles. The series of eclipses separated by a repeat of one of these intervals is called an eclipse series.
Eclipse conditions
Eclips ...
*Solar eclipse
A solar eclipse occurs when the Moon passes between Earth and the Sun, thereby obscuring the view of the Sun from a small part of the Earth, totally or partially. Such an alignment occurs during an eclipse season, approximately every six mo ...
* Lunar eclipse
*Metonic cycle
The Metonic cycle or enneadecaeteris (from grc, ἐννεακαιδεκαετηρίς, from ἐννεακαίδεκα, "nineteen") is a period of almost exactly 19 years after which the lunar phases recur at the same time of the year. The rec ...
References
Bibliography
* Jean Meeus and Hermann Mucke (1983) ''Canon of Lunar Eclipses''. Astronomisches Büro, Vienna * Theodor von Oppolzer (1887)''Canon der Finsternisse''
Vienna * Jean Meeus, ''Mathematical Astronomy Morsels'', Willmann-Bell, Inc., 1997 (Chapter 9, p. 51, Table 9. A Some eclipse Periodicities)
External links
List of all active saros cycles
– Interactive eclipse search
Eclipse Search
– Search 5,000 years of eclipse data by various attributes
– Fundamental astronomy of eclipses {{DEFAULTSORT:Saros cycle 1st-millennium BC introductions Eclipses Time in astronomy Technical factors of astrology Neo-Babylonian Empire Chaldea