sample space on:
[Wikipedia]
[Google]
[Amazon]
In 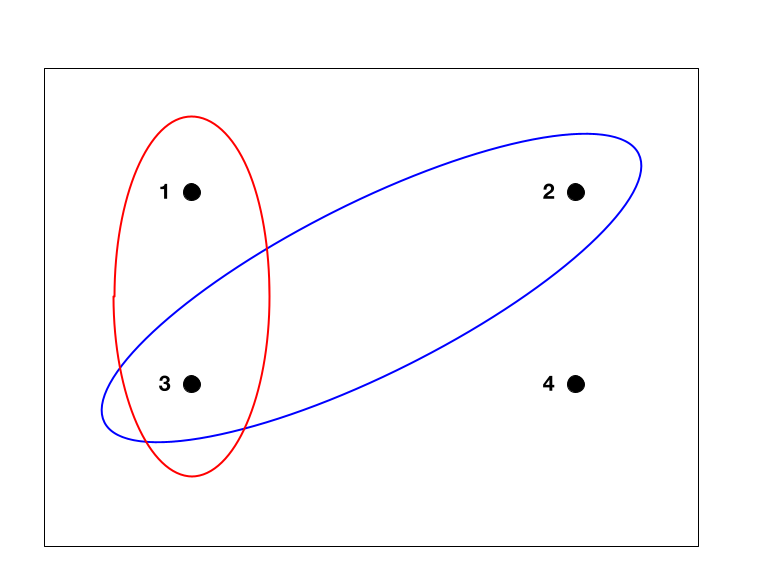 A sample space can be represented visually by a rectangle, with the outcomes of the sample space denoted by points within the rectangle. The events may be represented by ovals, where the points enclosed within the oval make up the event.
A sample space can be represented visually by a rectangle, with the outcomes of the sample space denoted by points within the rectangle. The events may be represented by ovals, where the points enclosed within the oval make up the event.

 Some treatments of probability assume that the various outcomes of an experiment are always defined so as to be equally likely. For any sample space with equally likely outcomes, each outcome is assigned the probability . However, there are experiments that are not easily described by a sample space of equally likely outcomes—for example, if one were to toss a thumb tack many times and observe whether it landed with its point upward or downward, there is no physical symmetry to suggest that the two outcomes should be equally likely.
Though most random phenomena do not have equally likely outcomes, it can be helpful to define a sample space in such a way that outcomes are at least approximately equally likely, since this condition significantly simplifies the computation of probabilities for events within the sample space. If each individual outcome occurs with the same probability, then the probability of any event becomes simply:
:
For example, if two fair six-sided dice are thrown to generate two uniformly distributed integers, and , each in the range from 1 to 6, inclusive, the 36 possible ordered pairs of outcomes constitute a sample space of equally likely events. In this case, the above formula applies, such as calculating the probability of a particular sum of the two rolls in an outcome. The probability of the event that the sum is five is , since four of the thirty-six equally likely pairs of outcomes sum to five.
If the sample space was the all of the possible sums obtained from rolling two six-sided dice, the above formula can still be applied because the dice rolls are fair, but the number of outcomes in a given event will vary. A sum of two can occur with the outcome , so the probability is . For a sum of seven, the outcomes in the event are , so the probability is .
Some treatments of probability assume that the various outcomes of an experiment are always defined so as to be equally likely. For any sample space with equally likely outcomes, each outcome is assigned the probability . However, there are experiments that are not easily described by a sample space of equally likely outcomes—for example, if one were to toss a thumb tack many times and observe whether it landed with its point upward or downward, there is no physical symmetry to suggest that the two outcomes should be equally likely.
Though most random phenomena do not have equally likely outcomes, it can be helpful to define a sample space in such a way that outcomes are at least approximately equally likely, since this condition significantly simplifies the computation of probabilities for events within the sample space. If each individual outcome occurs with the same probability, then the probability of any event becomes simply:
:
For example, if two fair six-sided dice are thrown to generate two uniformly distributed integers, and , each in the range from 1 to 6, inclusive, the 36 possible ordered pairs of outcomes constitute a sample space of equally likely events. In this case, the above formula applies, such as calculating the probability of a particular sum of the two rolls in an outcome. The probability of the event that the sum is five is , since four of the thirty-six equally likely pairs of outcomes sum to five.
If the sample space was the all of the possible sums obtained from rolling two six-sided dice, the above formula can still be applied because the dice rolls are fair, but the number of outcomes in a given event will vary. A sum of two can occur with the outcome , so the probability is . For a sum of seven, the outcomes in the event are , so the probability is .
probability theory
Probability theory is the branch of mathematics concerned with probability. Although there are several different probability interpretations, probability theory treats the concept in a rigorous mathematical manner by expressing it through a set o ...
, the sample space (also called sample description space, possibility space, or outcome space) of an experiment
An experiment is a procedure carried out to support or refute a hypothesis, or determine the efficacy or likelihood of something previously untried. Experiments provide insight into cause-and-effect by demonstrating what outcome occurs wh ...
or random trial
In law, a trial is a coming together of parties to a dispute, to present information (in the form of evidence) in a tribunal, a formal setting with the authority to adjudicate claims or disputes. One form of tribunal is a court. The tribun ...
is the set of all possible outcomes or results of that experiment. A sample space is usually denoted using set notation, and the possible ordered outcomes, or sample points, are listed as elements
Element or elements may refer to:
Science
* Chemical element, a pure substance of one type of atom
* Heating element, a device that generates heat by electrical resistance
* Orbital elements, parameters required to identify a specific orbit of ...
in the set. It is common to refer to a sample space by the labels ''S'', Ω, or ''U'' (for " universal set"). The elements of a sample space may be numbers, words, letters, or symbols. They can also be finite
Finite is the opposite of infinite. It may refer to:
* Finite number (disambiguation)
* Finite set, a set whose cardinality (number of elements) is some natural number
* Finite verb
Traditionally, a finite verb (from la, fīnītus, past partici ...
, countably
In mathematics, a Set (mathematics), set is countable if either it is finite set, finite or it can be made in one to one correspondence with the set of natural numbers. Equivalently, a set is ''countable'' if there exists an injective function fro ...
infinite, or uncountably infinite
In mathematics, an uncountable set (or uncountably infinite set) is an infinite set that contains too many elements to be countable. The uncountability of a set is closely related to its cardinal number: a set is uncountable if its cardinal num ...
.
A subset of the sample space is an event, denoted by . If the outcome of an experiment is included in , then event has occurred.
For example, if the experiment is tossing a single coin, the sample space is the set , where the outcome means that the coin is heads and the outcome means that the coin is tails. The possible events are , , and . For tossing two coins, the sample space is , where the outcome is if both coins are heads, if the first coin is heads and the second is tails, if the first coin is tails and the second is heads, and if both coins are tails. The event that at least one of the coins is heads is given by .
For tossing a single six-sided die one time, where the result of interest is the number of pips facing up, the sample space is .
A well-defined, non-empty sample space is one of three components in a probabilistic model (a probability space
In probability theory, a probability space or a probability triple (\Omega, \mathcal, P) is a mathematical construct that provides a formal model of a random process or "experiment". For example, one can define a probability space which models t ...
). The other two basic elements are: a well-defined set of possible events (an event space), which is typically the power set
In mathematics, the power set (or powerset) of a set is the set of all subsets of , including the empty set and itself. In axiomatic set theory (as developed, for example, in the ZFC axioms), the existence of the power set of any set is ...
of if is discrete or a σ-algebra on if it is continuous, and a probability
Probability is the branch of mathematics concerning numerical descriptions of how likely an Event (probability theory), event is to occur, or how likely it is that a proposition is true. The probability of an event is a number between 0 and ...
assigned to each event (a probability measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as ''countable additivity''. The difference between a probability measure and the more g ...
function).
 A sample space can be represented visually by a rectangle, with the outcomes of the sample space denoted by points within the rectangle. The events may be represented by ovals, where the points enclosed within the oval make up the event.
A sample space can be represented visually by a rectangle, with the outcomes of the sample space denoted by points within the rectangle. The events may be represented by ovals, where the points enclosed within the oval make up the event.
Conditions of a sample space
A set with outcomes (i.e. ) must meet some conditions in order to be a sample space: * The outcomes must be mutually exclusive, i.e. if occurs, then no other will take place, . * The outcomes must be collectively exhaustive, i.e. on every experiment (or random trial) there will always take place some outcome for . * The sample space () must have the right granularity depending on what the experimenter is interested in. Irrelevant information must be removed from the sample space and the rightabstraction
Abstraction in its main sense is a conceptual process wherein general rules and concepts are derived from the usage and classification of specific examples, literal ("real" or " concrete") signifiers, first principles, or other methods.
"An a ...
must be chosen.
For instance, in the trial of tossing a coin, one possible sample space is , where is the outcome where the coin lands heads and is for tails. Another possible sample space could be . Here, denotes a rainy day and is a day where it is not raining. For most experiments, would be a better choice than , as an experimenter likely do not care about how the weather affects the coin toss.
Multiple sample spaces
For many experiments, there may be more than one plausible sample space available, depending on what result is of interest to the experimenter. For example, when drawing a card from a standard deck of fifty-twoplaying card
A playing card is a piece of specially prepared card stock, heavy paper, thin cardboard, plastic-coated paper, cotton-paper blend, or thin plastic that is marked with distinguishing motifs. Often the front (face) and back of each card has a ...
s, one possibility for the sample space could be the various ranks (Ace through King), while another could be the suits (clubs, diamonds, hearts, or spades). A more complete description of outcomes, however, could specify both the denomination and the suit, and a sample space describing each individual card can be constructed as the Cartesian product
In mathematics, specifically set theory, the Cartesian product of two sets ''A'' and ''B'', denoted ''A''×''B'', is the set of all ordered pairs where ''a'' is in ''A'' and ''b'' is in ''B''. In terms of set-builder notation, that is
: A\ ...
of the two sample spaces noted above (this space would contain fifty-two equally likely outcomes). Still other sample spaces are possible, such as right-side up or upside down, if some cards have been flipped when shuffling.
Equally likely outcomes
 Some treatments of probability assume that the various outcomes of an experiment are always defined so as to be equally likely. For any sample space with equally likely outcomes, each outcome is assigned the probability . However, there are experiments that are not easily described by a sample space of equally likely outcomes—for example, if one were to toss a thumb tack many times and observe whether it landed with its point upward or downward, there is no physical symmetry to suggest that the two outcomes should be equally likely.
Though most random phenomena do not have equally likely outcomes, it can be helpful to define a sample space in such a way that outcomes are at least approximately equally likely, since this condition significantly simplifies the computation of probabilities for events within the sample space. If each individual outcome occurs with the same probability, then the probability of any event becomes simply:
:
For example, if two fair six-sided dice are thrown to generate two uniformly distributed integers, and , each in the range from 1 to 6, inclusive, the 36 possible ordered pairs of outcomes constitute a sample space of equally likely events. In this case, the above formula applies, such as calculating the probability of a particular sum of the two rolls in an outcome. The probability of the event that the sum is five is , since four of the thirty-six equally likely pairs of outcomes sum to five.
If the sample space was the all of the possible sums obtained from rolling two six-sided dice, the above formula can still be applied because the dice rolls are fair, but the number of outcomes in a given event will vary. A sum of two can occur with the outcome , so the probability is . For a sum of seven, the outcomes in the event are , so the probability is .
Some treatments of probability assume that the various outcomes of an experiment are always defined so as to be equally likely. For any sample space with equally likely outcomes, each outcome is assigned the probability . However, there are experiments that are not easily described by a sample space of equally likely outcomes—for example, if one were to toss a thumb tack many times and observe whether it landed with its point upward or downward, there is no physical symmetry to suggest that the two outcomes should be equally likely.
Though most random phenomena do not have equally likely outcomes, it can be helpful to define a sample space in such a way that outcomes are at least approximately equally likely, since this condition significantly simplifies the computation of probabilities for events within the sample space. If each individual outcome occurs with the same probability, then the probability of any event becomes simply:
:
For example, if two fair six-sided dice are thrown to generate two uniformly distributed integers, and , each in the range from 1 to 6, inclusive, the 36 possible ordered pairs of outcomes constitute a sample space of equally likely events. In this case, the above formula applies, such as calculating the probability of a particular sum of the two rolls in an outcome. The probability of the event that the sum is five is , since four of the thirty-six equally likely pairs of outcomes sum to five.
If the sample space was the all of the possible sums obtained from rolling two six-sided dice, the above formula can still be applied because the dice rolls are fair, but the number of outcomes in a given event will vary. A sum of two can occur with the outcome , so the probability is . For a sum of seven, the outcomes in the event are , so the probability is .
Simple random sample
In statistics, inferences are made about characteristics of apopulation
Population typically refers to the number of people in a single area, whether it be a city or town, region, country, continent, or the world. Governments typically quantify the size of the resident population within their jurisdiction using ...
by studying a sample of that population's individuals. In order to arrive at a sample that presents an unbiased estimate of the true characteristics of the population, statisticians often seek to study a simple random sample
In statistics, a simple random sample (or SRS) is a subset of individuals (a sample) chosen from a larger set (a population) in which a subset of individuals are chosen randomly, all with the same probability. It is a process of selecting a sam ...
—that is, a sample in which every individual in the population is equally likely to be included. The result of this is that every possible combination of individuals who could be chosen for the sample has an equal chance to be the sample that is selected (that is, the space of simple random samples of a given size from a given population is composed of equally likely outcomes).
Infinitely large sample spaces
In an elementary approach toprobability
Probability is the branch of mathematics concerning numerical descriptions of how likely an Event (probability theory), event is to occur, or how likely it is that a proposition is true. The probability of an event is a number between 0 and ...
, any subset of the sample space is usually called an event. However, this gives rise to problems when the sample space is continuous, so that a more precise definition of an event is necessary. Under this definition only measurable subsets of the sample space, constituting a σ-algebra over the sample space itself, are considered events.
An example of an infinitely large sample space is measuring the lifetime of a light bulb. The corresponding sample space would be .
See also
* Parameter space *Probability space
In probability theory, a probability space or a probability triple (\Omega, \mathcal, P) is a mathematical construct that provides a formal model of a random process or "experiment". For example, one can define a probability space which models t ...
* Space (mathematics)
* Set (mathematics)
A set is the mathematical model for a collection of different things; a set contains ''elements'' or ''members'', which can be mathematical objects of any kind: numbers, symbols, points in space, lines, other geometrical shapes, variables, or e ...
* Event (probability theory)
In probability theory, an event is a set of outcomes of an experiment (a subset of the sample space) to which a probability is assigned. A single outcome may be an element of many different events, and different events in an experiment are us ...
* σ-algebra
References
External links
* {{DEFAULTSORT:Sample Space Experiment (probability theory)