Root locus on:
[Wikipedia]
[Google]
[Amazon]
 In
In
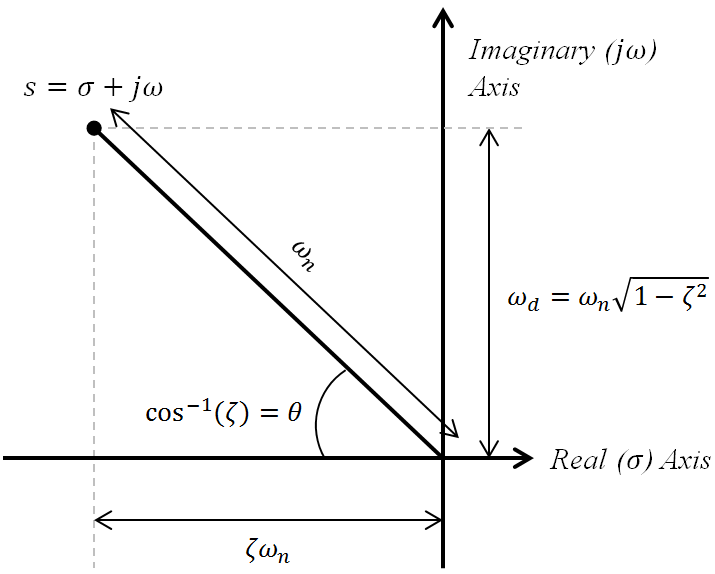 In addition to determining the stability of the system, the root locus can be used to design the
In addition to determining the stability of the system, the root locus can be used to design the
 For this system, the
For this system, the
% Manual method
K_array = (0:0.1:220).'; % .' is a transpose. Looking up in Matlab documentation.
NK = length(K_array);
x_array = zeros(NK, 3);
y_array = zeros(NK, 3);
for nK = 1:NK
K = K_array(nK);
C = , 3, (5 + K), (1 + 3*K)
r = roots(C).';
x_array(nK,:) = real(r);
y_array(nK,:) = imag(r);
end
figure();
plot(x_array, y_array);
grid on;
% Built-in method
sys = tf( , 3 , 3, 5, 1;
figure();
rlocus(sys);
 The following Python code can also be used to calculate and plot the root locus of the closed-loop transfer function using the Python Control Systems Library and Matplotlib.
The following Python code can also be used to calculate and plot the root locus of the closed-loop transfer function using the Python Control Systems Library and Matplotlib.
import control as ct
import matplotlib.pyplot as plt
# Define the transfer function
sys = ct.TransferFunction( , 3 , 3, 5, 1
# Calculate and plot the root locus
roots, gains = ct.root_locus(sys, plot=True)
plt.show()
Carnegie Mellon / University of Michigan Tutorial
* ttps://web.archive.org/web/20070301215842/http://www.atp.ruhr-uni-bochum.de/rt1/syscontrol/node46.html The root-locus method: Drawing by hand techniques
"RootLocs": A free multi-featured root-locus plotter for Mac and Windows platforms
Root Locus at ControlTheoryPro.com
* * ttp://reference.wolfram.com/mathematica/ref/RootLocusPlot.html Mathematica function for plotting the root locus* {{cite journal , last1=Šekara , first1=Tomislav B. , last2=Rapaić , first2=Milan R. , title=A revision of root locus method with applications , journal=Journal of Process Control , date=1 October 2015 , volume=34 , pages=26–34 , doi=10.1016/j.jprocont.2015.07.007 Classical control theory
 In
In control theory
Control theory is a field of control engineering and applied mathematics that deals with the control system, control of dynamical systems in engineered processes and machines. The objective is to develop a model or algorithm governing the applic ...
and stability theory
In mathematics, stability theory addresses the stability of solutions of differential equations and of trajectories of dynamical systems under small perturbations of initial conditions. The heat equation, for example, is a stable partial differ ...
, root locus analysis is a graphical method for examining how the roots of a system change with variation of a certain system parameter
A parameter (), generally, is any characteristic that can help in defining or classifying a particular system (meaning an event, project, object, situation, etc.). That is, a parameter is an element of a system that is useful, or critical, when ...
, commonly a gain within a feedback
Feedback occurs when outputs of a system are routed back as inputs as part of a chain of cause and effect that forms a circuit or loop. The system can then be said to ''feed back'' into itself. The notion of cause-and-effect has to be handle ...
system. This is a technique used as a stability criterion In control theory, and especially stability theory, a stability criterion establishes when a system is stable polynomial, stable. A number of stability criteria are in common use:
*Circle criterion
*Jury stability criterion
*Liénard–Chipart cri ...
in the field of classical control theory
Classical control theory is a branch of control theory that deals with the behavior of dynamical systems with inputs, and how their behavior is modified by feedback, using the Laplace transform as a basic tool to model such systems.
The usual ob ...
developed by Walter R. Evans which can determine stability
Stability may refer to:
Mathematics
*Stability theory, the study of the stability of solutions to differential equations and dynamical systems
** Asymptotic stability
** Exponential stability
** Linear stability
**Lyapunov stability
** Marginal s ...
of the system. The root locus plots the poles
Pole or poles may refer to:
People
*Poles (people), another term for Polish people, from the country of Poland
* Pole (surname), including a list of people with the name
* Pole (musician) (Stefan Betke, born 1967), German electronic music artist
...
of the closed loop transfer function in the complex ''s''-plane as a function of a gain parameter (see pole–zero plot
In mathematics, signal processing and control theory, a pole–zero plot is a graphical representation of a rational transfer function in the complex plane which helps to convey certain properties of the system such as:
* Stability
* Causal syst ...
).
Evans also invented in 1948 an analog computer
An analog computer or analogue computer is a type of computation machine (computer) that uses physical phenomena such as Electrical network, electrical, Mechanics, mechanical, or Hydraulics, hydraulic quantities behaving according to the math ...
to compute root loci, called a "Spirule" (after "spiral" and "slide rule
A slide rule is a hand-operated mechanical calculator consisting of slidable rulers for conducting mathematical operations such as multiplication, division, exponents, roots, logarithms, and trigonometry. It is one of the simplest analog ...
"); it found wide use before the advent of digital computer
A computer is a machine that can be programmed to automatically carry out sequences of arithmetic or logical operations (''computation''). Modern digital electronic computers can perform generic sets of operations known as ''programs'', wh ...
s.
Uses
damping ratio
In physical systems, damping is the loss of energy of an oscillating system by dissipation. Damping is an influence within or upon an oscillatory system that has the effect of reducing or preventing its oscillation. Examples of damping include ...
('' ζ'') and natural frequency
Natural frequency, measured in terms of '' eigenfrequency'', is the rate at which an oscillatory system tends to oscillate in the absence of disturbance. A foundational example pertains to simple harmonic oscillators, such as an idealized spring ...
(''ω''''n'') of a feedback system. Lines of constant damping ratio can be drawn radially from the origin and lines of constant natural frequency can be drawn as arccosine whose center points coincide with the origin. By selecting a point along the root locus that coincides with a desired damping ratio and natural frequency, a gain ''K'' can be calculated and implemented in the controller. More elaborate techniques of controller design using the root locus are available in most control textbooks: for instance, lag, lead, PI, PD and PID controllers can be designed approximately with this technique.
The definition of the damping ratio
In physical systems, damping is the loss of energy of an oscillating system by dissipation. Damping is an influence within or upon an oscillatory system that has the effect of reducing or preventing its oscillation. Examples of damping include ...
and natural frequency
Natural frequency, measured in terms of '' eigenfrequency'', is the rate at which an oscillatory system tends to oscillate in the absence of disturbance. A foundational example pertains to simple harmonic oscillators, such as an idealized spring ...
presumes that the overall feedback system is well approximated by a second order system; i.e. the system has a dominant pair of poles. This is often not the case, so it is good practice to simulate the final design to check if the project goals are satisfied.
Definition
The root locus of a feedback system is the graphical representation in the complex ''s''-plane of the possible locations of its closed-loop poles for varying values of a certain system parameter. The points that are part of the root locus satisfy the angle condition. The value of the parameter for a certain point of the root locus can be obtained using the magnitude condition. Suppose there is a feedback system with input signal and output signal . The forward pathtransfer function
In engineering, a transfer function (also known as system function or network function) of a system, sub-system, or component is a function (mathematics), mathematical function that mathematical model, models the system's output for each possible ...
is ; the feedback path transfer function is .
closed-loop transfer function
In control theory, a closed-loop transfer function is a mathematical function describing the net result of the effects of a feedback control loop on the input signal to the plant under control.
Overview
The closed-loop transfer function is mea ...
is given by
:
Thus, the closed-loop poles of the closed-loop transfer function are the roots of the characteristic equation . The roots of this equation may be found wherever .
In systems without pure delay, the product is a rational polynomial function and may be expressed as
:
where are the zeros, are the poles, and is a scalar gain. Typically, a root locus diagram will indicate the transfer function's pole locations for varying values of the parameter . A root locus plot will be all those points in the ''s''-plane where for any value of .
The factoring of and the use of simple monomials means the evaluation of the rational polynomial can be done with vector techniques that add or subtract angles and multiply or divide magnitudes. The vector formulation arises from the fact that each monomial term in the factored represents the vector from to in the s-plane. The polynomial can be evaluated by considering the magnitudes and angles of each of these vectors.
According to vector mathematics, the angle of the result of the rational polynomial is the sum of all the angles in the numerator minus the sum of all the angles in the denominator. So to test whether a point in the ''s''-plane is on the root locus, only the angles to all the open loop poles and zeros need be considered. This is known as the angle condition.
Similarly, the magnitude of the result of the rational polynomial is the product of all the magnitudes in the numerator divided by the product of all the magnitudes in the denominator. It turns out that the calculation of the magnitude is not needed to determine if a point in the s-plane is part of the root locus because varies and can take an arbitrary real value. For each point of the root locus a value of can be calculated. This is known as the magnitude condition.
The root locus only gives the location of closed loop poles as the gain is varied. The value of does not affect the location of the zeros. The open-loop zeros are the same as the closed-loop zeros.
Angle condition
A point of the complex ''s''-plane satisfies the angle condition if : which is the same as saying that : that is, the sum of the angles from the open-loop zeros to the point (measured per zero w.r.t. a horizontal running through that zero) minus the angles from the open-loop poles to the point (measured per pole w.r.t. a horizontal running through that pole) has to be equal to , or 180 degrees. Note that these interpretations should not be mistaken for the angle differences between the point and the zeros/poles.Magnitude condition
A value of satisfies the magnitude condition for a given point of the root locus if : which is the same as saying that :.Sketching root locus
Using a few basic rules, the root locus method can plot the overall shape of the path (locus) traversed by the roots as the value of varies. The plot of the root locus then gives an idea of the stability and dynamics of this feedback system for different values of . The rules are the following: * Mark open-loop poles and zeros * Mark real axis portion to the left of an odd number of poles and zeros * Findasymptote
In analytic geometry, an asymptote () of a curve is a line such that the distance between the curve and the line approaches zero as one or both of the ''x'' or ''y'' coordinates tends to infinity. In projective geometry and related contexts, ...
s
Let ''P'' be the number of poles and ''Z'' be the number of zeros:
:
The asymptotes intersect the real axis at (which is called the centroid) and depart at angle given by:
:
:
where is the sum of all the locations of the poles, is the sum of all the locations of the explicit zeros and denotes that we are only interested in the real part.
* Phase condition on test point to find angle of departure
* Compute breakaway/break-in points
The breakaway points are located at the roots of the following equation:
:
Once you solve for ''z'', the real roots give you the breakaway/reentry points. Complex roots correspond to a lack of breakaway/reentry.
Plotting root locus
Given the general closed-loop denominator rational polynomial : the characteristic equation can be simplified to : The solutions of to this equation are the root loci of the closed-loop transfer function.Example
Given : we will have the characteristic equation : The following MATLAB code will plot the root locus of the closed-loop transfer function as varies using the described manual method as well as therlocus built-in function:
 The following Python code can also be used to calculate and plot the root locus of the closed-loop transfer function using the Python Control Systems Library and Matplotlib.
The following Python code can also be used to calculate and plot the root locus of the closed-loop transfer function using the Python Control Systems Library and Matplotlib.''z''-plane versus ''s''-plane
The root locus method can also be used for the analysis ofsampled data systems In systems science, a sampled-data system is a control system in which a continuous-time plant is controlled with a digital device. Under periodic sampling, the sampled-data system is time-varying but also periodic; thus, it may be modeled by a si ...
by computing the root locus in the ''z''-plane, the discrete counterpart of the ''s''-plane. The equation maps continuous ''s''-plane poles (not zeros) into the ''z''-domain, where is the sampling period. The stable, left half ''s''-plane maps into the interior of the unit circle of the ''z''-plane, with the ''s''-plane origin equating to '', z, '' = 1 (because ''e''0 = 1). A diagonal line of constant damping in the ''s''-plane maps around a spiral from (1,0) in the ''z'' plane as it curves in toward the origin. The Nyquist aliasing
In signal processing and related disciplines, aliasing is a phenomenon that a reconstructed signal from samples of the original signal contains low frequency components that are not present in the original one. This is caused when, in the ori ...
criteria is expressed graphically in the ''z''-plane by the ''x''-axis, where . The line of constant damping just described spirals in indefinitely but in sampled data systems, frequency content is aliased down to lower frequencies by integral multiples of the Nyquist frequency
In signal processing, the Nyquist frequency (or folding frequency), named after Harry Nyquist, is a characteristic of a Sampling (signal processing), sampler, which converts a continuous function or signal into a discrete sequence. For a given S ...
. That is, the sampled response appears as a lower frequency and better damped as well since the root in the ''z''-plane maps equally well to the first loop of a different, better damped spiral curve of constant damping. Many other interesting and relevant mapping properties can be described, not least that ''z''-plane controllers, having the property that they may be directly implemented from the ''z''-plane transfer function (zero/pole ratio of polynomials), can be imagined graphically on a ''z''-plane plot of the open loop transfer function, and immediately analyzed utilizing root locus.
Since root locus is a graphical angle technique, root locus rules work the same in the and planes.
The idea of a root locus can be applied to many systems where a single parameter is varied. For example, it is useful to sweep any system parameter for which the exact value is uncertain in order to determine its behavior.
See also
*Phase margin
In electronic amplifiers, the phase margin (PM) is the difference between the phase (waves), phase lag (< 0) and -180°, for an amplifier's output signal (relative to its input) at zero dB gain - i.e. unity gain, or that the output signal has the ...
* Routh–Hurwitz stability criterion
In the control theory, control system theory, the Routh–Hurwitz stability criterion is a mathematical test that is a necessary and sufficient condition for the stable polynomial, stability of a linear time-invariant system, linear time-invarian ...
* Nyquist stability criterion
In control theory and stability theory, the Nyquist stability criterion or Strecker–Nyquist stability criterion, independently discovered by the German electrical engineer at Siemens in 1930 and the Swedish-American electrical engineer Harry ...
* Gain and phase margin
* Bode plot
In electrical engineering and control theory, a Bode plot is a graph of the frequency response of a system. It is usually a combination of a Bode magnitude plot, expressing the magnitude (usually in decibels) of the frequency response, and a B ...
References
*Further reading
* * * * * *External links
* Wikibooks: Control Systems/Root LocusCarnegie Mellon / University of Michigan Tutorial
* ttps://web.archive.org/web/20070301215842/http://www.atp.ruhr-uni-bochum.de/rt1/syscontrol/node46.html The root-locus method: Drawing by hand techniques
"RootLocs": A free multi-featured root-locus plotter for Mac and Windows platforms
Root Locus at ControlTheoryPro.com
* * ttp://reference.wolfram.com/mathematica/ref/RootLocusPlot.html Mathematica function for plotting the root locus* {{cite journal , last1=Šekara , first1=Tomislav B. , last2=Rapaić , first2=Milan R. , title=A revision of root locus method with applications , journal=Journal of Process Control , date=1 October 2015 , volume=34 , pages=26–34 , doi=10.1016/j.jprocont.2015.07.007 Classical control theory